每個(gè)分支節(jié)點(diǎn)的第一個(gè)字段是到以其為根的subtrie中元素(譯注:應(yīng)該是指子節(jié)點(diǎn))的引用.我們可以用被引用的元素的首字符的索引代替元素引用.圖3展示了替換后的樹.我們將會(huì)用這種修改后的形式作為后綴樹的表示.
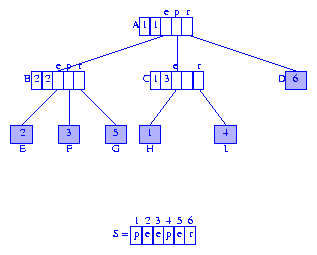
Figure 3 Suffix tree for peeper
如果后綴樹的每條邊用從分支節(jié)點(diǎn)到其子節(jié)點(diǎn)的字符(串)標(biāo)注,可以更容易描述后綴樹的查找和構(gòu)建算法.標(biāo)簽的第一個(gè)字符用來確定要移到哪一個(gè)子節(jié)點(diǎn),剩余的字符表示要跳過的字符(串).圖4展示的就是圖3用這種方式畫出后得到的后綴樹.
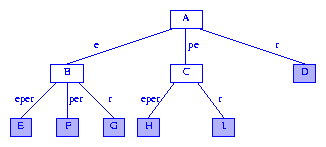
Figure 4 A more humane drawing of a suffix tree
在后綴樹的更直觀的畫法中,從任意根節(jié)點(diǎn)到信息節(jié)點(diǎn)的路徑上所有邊的標(biāo)簽拼接在一起得到的就是信息節(jié)點(diǎn)表示的后綴.When the digit number for the root is not 1, the humane drawing of a suffix tree includes a head node with an edge to the former root. This edge is labeled with the digits that are skipped over.
后綴樹的某個(gè)節(jié)點(diǎn)表示的字符串是由根節(jié)點(diǎn)到此節(jié)點(diǎn)的路徑上的標(biāo)簽拼出來的.圖4中的節(jié)點(diǎn)A表示空串epsilon,節(jié)點(diǎn)C表示字符串pe,節(jié)點(diǎn)F表示字符串eper.
由于后綴樹的關(guān)鍵字長度不同,我們必須保證沒有一個(gè)關(guān)鍵字是另一個(gè)的真前綴(proper prefix).當(dāng)字符串S的最后一個(gè)字符在S中只出現(xiàn)一次,就不會(huì)出現(xiàn)S的其中一個(gè)后綴是另一個(gè)后綴的真前綴的情況.在字符串peeper中,最后的字符是r,并且只出現(xiàn)了一次.因此peeper的后綴中就不會(huì)出現(xiàn)真前綴的情況.字符串data的最后字符是a,并且出現(xiàn)了兩次.因此,data有兩個(gè)以a開始的后綴,ata和a.后綴a是ata的真前綴.
當(dāng)字符串S的最后字符在S中出現(xiàn)多于一次,就必須在S的所有后綴后面附加一個(gè)新的字符(比如說#),這樣任何一個(gè)后綴都不會(huì)是其他后綴的前綴.還有一種方法是,我們可以在S后面附加新的字符#,得到新的串$#,然后創(chuàng)建$#的后綴樹.這樣做之后得到的后綴樹比直接在S的每個(gè)后綴后面附加#會(huì)多一個(gè)后綴#.
讓我們查找那個(gè)子串吧
但是，首先要說明幾個(gè)術(shù)語
用n=|S|表示要?jiǎng)?chuàng)建后綴樹的字符串的長度.我們從左到右依次給S的字符編號(hào),最左邊的編號(hào)為1.S[i]表示S的第i個(gè)字符,suffix(i)表示從字符i開始的后綴S[i]...S[n],1<=i<=n.
關(guān)于查找
當(dāng)在S中查找模式P時(shí),用到的一個(gè)基本的觀察(observation)是P在S中出現(xiàn)當(dāng)且僅當(dāng)P是S的某個(gè)后綴的前綴.
假設(shè)P = P[1]...P[k] = S[i]...S[i+k-1].則P是suffix(i)的前綴.既然suffix(i)在我們的壓縮trie樹中(也就是后綴樹),我們可以利用在壓縮trie樹中查找關(guān)鍵字前綴的策略來查找P.
讓我們?cè)谧址?font color="#3366ff">S=peeper中查找模式
P=per.假設(shè)我們已經(jīng)為S創(chuàng)建好了后綴樹(圖4).查找從根結(jié)點(diǎn)A開始.因?yàn)镻[1]=p,我們順著標(biāo)簽以p開始的邊.當(dāng)順著此邊繼續(xù)時(shí),我們對(duì)邊標(biāo)簽的剩余字符和P的后續(xù)字符做比較.由于標(biāo)簽的剩余字符跟P的字符相符,我們到達(dá)分支C.在到達(dá)C的過程中,我們已經(jīng)使用了P的前兩個(gè)字符.第三個(gè)字符是r,因此我們從節(jié)點(diǎn)C順著以r開始的邊繼續(xù).由于這條邊沒有其他字符,因此不需要其他比較,到達(dá)信息節(jié)點(diǎn)I.這時(shí),P中的字符已經(jīng)用完了,我們就斷定P在S中.由于已經(jīng)到達(dá)信息節(jié)點(diǎn)I,我們斷定P實(shí)際上是S的后綴.在實(shí)際的后綴樹表示中(而不是如圖4這種人性化的表示),信息節(jié)點(diǎn)I包含索引4,這告訴我們模式P=per由S=peeper的第4個(gè)字符開始(也就是說,P=suffix(4)).更進(jìn)一步,我們可以得到P在S中只出現(xiàn)一次;如果一個(gè)模式在字符串中出現(xiàn)多次,查找會(huì)在分支節(jié)點(diǎn)中止,而不是信息節(jié)點(diǎn).(譯注:例如查找pe,查找在節(jié)點(diǎn)C中止,說明它在S中出現(xiàn)了兩次--C有兩個(gè)葉子節(jié)點(diǎn))
現(xiàn)在我們來查找模式
P=eeee.還是從根結(jié)點(diǎn)開始.由于P的第一個(gè)字符是e,我們沿著以e開始的邊到達(dá)B.下一個(gè)字符還是e,因此我們從B開始沿著以e開始的邊繼續(xù).在沿著這條邊向下的過程中,我們需要比較邊標(biāo)簽的剩余字符per和P的剩余字符ee.比較第一對(duì)字符(p,e)時(shí)無法匹配,因此我們斷定P不在S中.
假設(shè)我們查找模式
P=p.從根開始,沿著以p開始的邊往下.在向下的過程中,我們比較邊的剩余字符(只有字符e)和模式的剩余字符.由于已經(jīng)到P的結(jié)尾,我們斷定P是以節(jié)點(diǎn)C為根的subtrie的所有關(guān)鍵字的前綴.可以通過遍歷以C為根的subtrie、訪問subtrie的所有信息節(jié)點(diǎn)找到P出現(xiàn)的所有位置。如果只需要P出現(xiàn)的一個(gè)位置，可以利用存儲(chǔ)在節(jié)點(diǎn)C的第一部分的索引。當(dāng)沿著到節(jié)點(diǎn)X的邊查找時(shí)模式結(jié)束，我們就說已到達(dá)節(jié)點(diǎn)X；查找在節(jié)點(diǎn)X結(jié)束。
當(dāng)查找模式
P=rope，利用P的第一個(gè)字符r到達(dá)信息節(jié)點(diǎn)D。由于模式還沒有結(jié)束，我們必須根據(jù)D的字符檢查P的剩余字符。檢查顯示P不是D的關(guān)鍵字的前綴，因此P不在S=peeper中。
我們要做的最后一個(gè)查找是對(duì)模式P=pepe。從圖4的根結(jié)點(diǎn)開始，我們沿著以p開始的邊到達(dá)節(jié)點(diǎn)C。下一個(gè)未檢查的字符是p。因此，從C開始，我們希望沿著以p開始的邊繼續(xù)。由于沒有滿足這個(gè)條件的邊，我們斷定pepe不在peeper中。
Other Nifty Things You Can Do with a Suffix Tree一旦為字符串S創(chuàng)建好了后綴樹，我們就可以在O(|P|)時(shí)間內(nèi)判斷S是否包含P。這意味著如果為莎士比亞的戲劇“羅密歐與朱麗葉”的內(nèi)容創(chuàng)建了后綴樹，我們就可以非常快的判斷文章中是否存在短語wherefore art thou。事實(shí)上，只需話費(fèi)比較18個(gè)字符的時(shí)間（模式的長度）。查找時(shí)間跟文章的長度無關(guān)。
其他可以快速完成的有趣事情：
1.查找模式P的所有出現(xiàn)。這是通過對(duì)P查找后綴樹實(shí)現(xiàn)。如果P至少出現(xiàn)一次，查找會(huì)在信息節(jié)點(diǎn)或者分支節(jié)點(diǎn)中止。當(dāng)中止于信息節(jié)點(diǎn)時(shí)，P只出現(xiàn)一次。如果中止于分支節(jié)點(diǎn)X，模式出現(xiàn)的所有地方可以通過訪問以X為根的subtrie的信息節(jié)點(diǎn)來得到。如果我們按照下面的方式，這個(gè)訪問操作可以在O(n)（n是模式出現(xiàn)的次數(shù)）時(shí)間內(nèi)完成。
(a)
將所有的信息節(jié)點(diǎn)按照節(jié)點(diǎn)所表示的后綴的字典序鏈起來（這也是從左到右掃描信息節(jié)點(diǎn)時(shí)遇到這些節(jié)點(diǎn)的順序）。圖4的信息節(jié)點(diǎn)會(huì)按照
E,F,G,H,I,D的順序鏈接起來。
(b)
在每個(gè)分支節(jié)點(diǎn)內(nèi)，保存以此節(jié)點(diǎn)為根的subtrie的第一個(gè)和最后一個(gè)信息節(jié)點(diǎn)的引用。圖4中節(jié)點(diǎn)A,B和C分別保存序?qū)?E,D),(E,G)和(H,I)。我們用序?qū)?firstInformationNode, lastInformationNode)周游以firstInformationNode開始、以lastInformationNode結(jié)束的鏈。這個(gè)周游會(huì)得到模式P出現(xiàn)的所有位置。注意，當(dāng)我們?cè)诜种Ч?jié)點(diǎn)中保存序?qū)?firstInformationNode, lastInformationNode)時(shí)，就不需要再保存到subtrie中的信息節(jié)點(diǎn)的引用（也就是字段element）。
2.查找包含模式P的所有字符串。假設(shè)我們有一些字符串
S1,S2,... Sk，我們想得到所有包含P的字符串。例如，基因庫中包含數(shù)以萬計(jì)的字符串，當(dāng)一個(gè)研究員提交一個(gè)查詢字符串，我們就要報(bào)告所有包含此模式的字符串。為了有效的執(zhí)行這類查詢，就需要?jiǎng)?chuàng)建一個(gè)包含字符串
S1$S2$...$Sk#的所有后綴的壓縮trie樹（也稱為多字符串后綴樹），這里的$,#是兩個(gè)不在字符串S1, S2, ..., Sk中出現(xiàn)的不同字符。在后綴樹的每個(gè)（分支）結(jié)點(diǎn)N中，保存所有的字符串Si的鏈表，其中Si是以N為根的subtrie中所有的信息節(jié)點(diǎn)表示的字符串的開始點(diǎn)位于其中的字符串（譯注：真拗口啊，這兒的意思就是對(duì)某個(gè)信息節(jié)點(diǎn)L，如果L表示的字符串從Si的某個(gè)位置開始，那就將Si的引用放到L的父輩節(jié)點(diǎn)的鏈表中）。
3.查找S中出現(xiàn)次數(shù)至少為m>1次的子串。這個(gè)查詢可以按照下面的方式在O(|S|)時(shí)間內(nèi)完成：
(a)周游后綴樹，對(duì)每個(gè)分支節(jié)點(diǎn)X，保存從根節(jié)點(diǎn)到X節(jié)點(diǎn)的字符串的長度l和以X為根的subtrie中信息節(jié)點(diǎn)的數(shù)目m。
(b)周游后綴樹，訪問信息節(jié)點(diǎn)數(shù)>=m的分支節(jié)點(diǎn)。l最大的分支節(jié)點(diǎn)表示的就是出現(xiàn)次數(shù)>=m的最長子串。
注意步驟(a)只需要執(zhí)行一次。完成后，我們可以對(duì)需要的任意m執(zhí)行步驟(b)。另外還要注意，當(dāng)m=2是，不需要確定subtrie中信息節(jié)點(diǎn)的數(shù)目。在后綴樹中，每個(gè)分支節(jié)點(diǎn)之后有兩個(gè)信息節(jié)點(diǎn)。
4.查找字符串S和T的最長公共子串。這可以按照下面的方式在
O(|S|+|T|)時(shí)間內(nèi)完成：
(a)為S和T創(chuàng)建多字符串后綴樹（也就是
S$T#的后綴樹）
(b)周游后綴樹，查找表示的字符串最長，并且以其為根的subtrie的信息節(jié)點(diǎn)表示的字符串中，至少有一個(gè)從S開始，另一個(gè)從T開始的字符串。
注意，有個(gè)相關(guān)的查找S和T的最長公共子序列的問題用動(dòng)態(tài)規(guī)劃算法在
O(|S|*|T|)時(shí)間內(nèi)完成。
如何創(chuàng)建你自己的后綴樹三個(gè)觀察(observation)
為了更有效的創(chuàng)建后綴樹，我們?yōu)槊總€(gè)分支節(jié)點(diǎn)添加字段longestProperSuffix。表示非空字符串Y的分支節(jié)點(diǎn)的longestProperSuffix字段指向表示Y的最長真后綴的分支節(jié)點(diǎn)（Y的最長真后綴通過去掉Y的首字符得到）。根結(jié)點(diǎn)的longestProperSuffix未使用。
圖5表示的是給圖4加上最長真后綴指針后得到（經(jīng)常將最長真后綴指針簡稱為后綴指針）。后綴指針用紅色箭頭表示。節(jié)點(diǎn)C表示字符串pe。pe的最長后綴e由節(jié)點(diǎn)B表示。因此C的后綴指針指向B。e的最長后綴是空串。由于根結(jié)點(diǎn)A表示空串，因此B的后綴指針指向A。
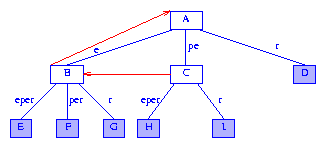
Figure 5 Suffix tree of Figure 4 augmented with suffix pointers
觀察1 如果S的后綴樹有一個(gè)表示字符串Y的分支節(jié)點(diǎn)，那么后綴樹中也有一個(gè)表示Y的最長后綴Z的分支節(jié)點(diǎn)。
證明 設(shè)P為表示Y的分支節(jié)點(diǎn)。由于P是分支節(jié)點(diǎn)，至少有兩個(gè)不同的字符x和y，使得S中有兩個(gè)分別以Yx和Yy開始的后綴。因此，S有兩個(gè)分別以Zx和Zy開始的后綴。因此，S的后綴樹中必然有一個(gè)對(duì)應(yīng)Z的分支節(jié)點(diǎn)。
觀察2 如果S的后綴樹有一個(gè)表示Y的分支節(jié)點(diǎn)，那么樹中對(duì)Y的每個(gè)后綴都有一個(gè)對(duì)應(yīng)的分支節(jié)點(diǎn)。
證明 由觀察1即可得到。
注意圖5中有一個(gè)表示pe的分支節(jié)點(diǎn)。因此，樹中一定有表示e和epsilon的分支節(jié)點(diǎn)。
在描述后綴樹的創(chuàng)建算法時(shí)，有兩個(gè)概念很有用：last branch node和last branch index。后綴suffix(i)的last branch node是表示suffix(i)的信息節(jié)點(diǎn)的父節(jié)點(diǎn)。在圖5中，suffix(1)...suffix(6)的last branch node分別是C,B,B,C,B和A。對(duì)任意后綴suffix(i)，其last branch index lastBranchIndex(i)是在suffix(i)的last branch node中，產(chǎn)生分支的字符的索引。在圖5中，lastBranchIndex(1)＝3,因?yàn)椋簊uffix(1)=peeper，suffix(1)由信息節(jié)點(diǎn)H表示，H的父節(jié)點(diǎn)是C；C的分支是在suffix(1)的第三個(gè)字符產(chǎn)生的；suffix(1)的第三個(gè)字符是S[3]。可以驗(yàn)證一下，lastBranIndex[1:6] = [3,3,4,6,6,6]。
觀察3 在S的后綴樹中， lastBranchIndex(i) <= lastBranchIndex(i+1), 1 <= i < n。
證明作為練習(xí)。
Get Out That Hammer and Saw, and Start Building
為了創(chuàng)建你自己的后綴樹，你必須由你自己的字符串開始。我們使用R = ababbabbaabbabb來闡述后綴樹的構(gòu)建過程。由于R的最后字符b出現(xiàn)了不止一次，我們?cè)赗后面附加字符#，為新的字符串S=R#創(chuàng)建后綴樹。
創(chuàng)建策略
后綴樹的創(chuàng)建算法從表示空串的根結(jié)點(diǎn)開始。根結(jié)點(diǎn)是一個(gè)分支節(jié)點(diǎn)。創(chuàng)建后綴樹過程的任何時(shí)候，都有一個(gè)分支節(jié)點(diǎn)被指定位活動(dòng)節(jié)點(diǎn)(active node)。這是插入下一個(gè)后綴的起始節(jié)點(diǎn)。用activeLength表示根結(jié)點(diǎn)對(duì)應(yīng)的字符串的長度。開始時(shí)，根節(jié)點(diǎn)是活動(dòng)節(jié)點(diǎn)，activeLength=0。圖6展示了開始時(shí)的狀態(tài)，綠色的節(jié)點(diǎn)是活動(dòng)節(jié)點(diǎn)。
Figure 6 Initial configuration for suffix tree construction
隨著處理的進(jìn)行，我們會(huì)不斷往樹中添加分支節(jié)點(diǎn)和信息節(jié)點(diǎn)。新添加的分支節(jié)點(diǎn)用品紅色表示，新添加的信息節(jié)點(diǎn)用青色表示。后綴指針為紅色。
后綴按照suffix(1), suffix(2), ..., suffix(n)的順序依次插入到樹中。后綴以這種順序插入是通過從左到右掃描字符串S的方氏完成。用tree(i)表示插入后綴suffix(1), ..., suffix(i)之后形成的樹，lastBranchIndex(j, i)表示tree(i)中后綴suffix(j)的last branch index。minDistance表示從活動(dòng)節(jié)點(diǎn)到即將插入的后綴的last branch index的距離的下界（譯注：感覺這個(gè)東西在實(shí)現(xiàn)的時(shí)候沒啥意義）。開始時(shí)，minDistance = 0并且lastBranchIndex(1,1) = 1。當(dāng)插入suffix(i)時(shí)，滿足條件lastBranchIndex(i,i) >= i + activeLength + minDistance。
為了向tree(i)中插入suffix(i+1)，我們必須遵循如下步驟：
1.確定lastBranchIndex(i+1, i+1)。為了完成這點(diǎn)，我們從當(dāng)前活動(dòng)節(jié)點(diǎn)開始。新后綴的開始的activeLength個(gè)字符（也就是字符S[i+1], S[i+2], ..., S[i + activeLength]）已知是跟當(dāng)前活動(dòng)節(jié)點(diǎn)表示的字符串相匹配的。因此，為了確定lastBranchIndex(i+1,i+1)，需要檢測(cè)新后綴的activeLength + 1, activeLength + 2, ...字符。這些字符用于確定tree(i)中進(jìn)一步處理時(shí)要經(jīng)過的路徑，此路徑始于活動(dòng)節(jié)點(diǎn)，當(dāng)lastBranchIndex(i+1,i+1)確定時(shí)中止。根據(jù)已知的lastBranchIndex(i+1,i+1) >= i + 1 + activeLength + minDistance，這個(gè)過程可以簡化，從而得到效率提升。
2.如果tree(i)中沒有表示字符串S[i]...S[lastBranchIndex(i+1,i+1)-1]的節(jié)點(diǎn)X，則創(chuàng)建一個(gè)。
3.為suffix(i+1)添加一個(gè)信息節(jié)點(diǎn)。這個(gè)信息節(jié)點(diǎn)是X的孩子，從X到信息節(jié)點(diǎn)的邊上的標(biāo)簽是S[lastBranchIndex(i+1, i+1)]...S[n]。
回到例子
我們從向圖6中的樹tree(0)插入suffix(1)開始。根結(jié)點(diǎn)是活動(dòng)節(jié)點(diǎn)，activeLength = minDistance = 0。suffix(1)的第一個(gè)字符是S[1]=a。從tree(0)的活動(dòng)節(jié)點(diǎn)開始沒有以a開始的邊（事實(shí)上，此時(shí)活動(dòng)節(jié)點(diǎn)沒有任何邊）。因此，lastBranchIndex(1,1) = 1。我們創(chuàng)建一個(gè)新的信息節(jié)點(diǎn)和一條邊，邊的標(biāo)簽是整個(gè)字符串。圖7展示了結(jié)果tree(1)。根結(jié)點(diǎn)依然是活動(dòng)節(jié)點(diǎn)，activeLength和minDistance沒有變化。
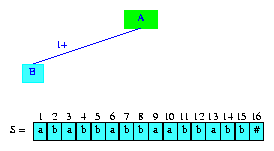
Figure 7 After the insertion of the suffix ababbabbaabbabb#
在我們的畫法中，信息節(jié)點(diǎn)的入邊的標(biāo)簽標(biāo)記為i+，i表示標(biāo)簽在S中的開始位置，+表示標(biāo)簽一直到字符串的結(jié)尾。因此，在圖7中，1+表示字符串S[1]...S[n]。圖7也展示了字符串S。新插入的后綴用青色表示。
為了插入后綴suffix(2)，我們?cè)俅螐母Y(jié)點(diǎn)開始檢查后綴的activeLength + 1 = 1, activeLength + 2 = 2, ...,字符。因?yàn)閟uffix(2)的第一個(gè)字符是S[2]=b，活動(dòng)節(jié)點(diǎn)沒有以S[2]=b開始的邊，所以lastBranchIndex(2,2) = 2。因此我們創(chuàng)建新的信息節(jié)點(diǎn)和標(biāo)記為2+的邊。結(jié)果如圖8所示。根結(jié)點(diǎn)依然是活動(dòng)節(jié)點(diǎn)，activeLength和minDistance依舊沒有變化。
Figure 8 After the insertion of the suffix babbabbaabbabb#
注意圖8是關(guān)于suffix(1)和suffix(2)的壓縮trie樹tree(2)。
下一個(gè)后綴suffix(3)開始于S[3]=a。由于tree(2)的活動(dòng)節(jié)點(diǎn)有一個(gè)以a開始的邊，所以lastBranchIndex(3,3) > 3。為了確定lastBranchIndex(3,3)，必需要查看suffix(3)的更過字符。尤其是，我們需要查看盡可能多的字符，以便區(qū)分suffix(1)和suffix(3)。首先比較后綴的第二個(gè)字符S[4]=b和邊1+的第二個(gè)字符S[2]=b。由于S[4]=S[2]，必須做進(jìn)一步的比較。下一步比較S[5]和S[3]。由于這兩個(gè)字符不同，我們可以確定lastBranchIndex(3,3)是5。這時(shí)，我們需要更新minDistance為2.注意，因?yàn)閘astBranchIndex(3,3) = 5 = 3 + activeLength + minDistance，這是minDistance的最大可能值。
為了插入suffix(3)，我們將tree(2)的邊1+一分為二。第一條邊的標(biāo)簽是1,2;第一條邊的標(biāo)簽是3+。這兩個(gè)邊之間插入新的分支節(jié)點(diǎn)。另外，還要為新插入的后綴添加信息節(jié)點(diǎn)。結(jié)果如圖9所示。邊標(biāo)簽1,2顯示為字符S[1]S[2] = ab。
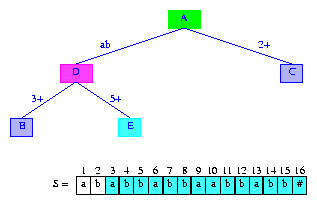
Figure 9 After the insertion of the suffix abbabbaabbabb#
tree(3)還沒完成，因?yàn)檫€沒有確定新加的分支節(jié)點(diǎn)的后綴指針。這個(gè)分支節(jié)點(diǎn)的最長后綴是b，但是對(duì)應(yīng)b的分支節(jié)點(diǎn)不存在。別驚慌，下一個(gè)要?jiǎng)?chuàng)建的分支節(jié)點(diǎn)就是對(duì)應(yīng)b的節(jié)點(diǎn)。
下一個(gè)要插入的后綴是suffix(4)。這是剛插入的suffix(3)的最長后綴。新后綴的插入過程由根據(jù)當(dāng)前活動(dòng)節(jié)點(diǎn)的后綴指針確定新的活動(dòng)節(jié)點(diǎn)開始。由于根結(jié)點(diǎn)沒有后綴指針，活動(dòng)節(jié)點(diǎn)沒有變化。因此activeLength也沒有變化。但是，我們必須更新minDistance以滿足lastBranchIndex(4,4) >= 4 + activeLength + minDistance。顯然，對(duì)于所有的i<= lastBranchIndex(i+1,i+1)。因此，lastBranchIndex(i+1,i+1) >= lastBranchIndex(i,i) >= i + activeLength + minDistance。為了保證lastBranchIndex(i+1,i+1) >= i + 1 + activeLength + minDistance，我們必須將minDistance減小1.
因?yàn)閙inDistance = 1，我們從活動(dòng)節(jié)點(diǎn)開始，沿著S[4]S[5]...指定的路徑記錄。我們不需要比較開始的minDistance個(gè)字符，因?yàn)樵趍inDistance+1之前的字符都已經(jīng)保證是匹配的了。由于活動(dòng)節(jié)點(diǎn)以S[4]=b開始的邊的長度大于1,我們比較S[5]和邊的第二個(gè)字符S[3]。因?yàn)檫@兩個(gè)字符不同，這條邊也要一分為二。第一條邊的標(biāo)簽為2,2=b；第二條棉的標(biāo)簽為3+。在兩條邊之間添加新的分支節(jié)點(diǎn)F，還要為新插入的后綴創(chuàng)建信息節(jié)點(diǎn)G。G跟F之間通過標(biāo)簽為5+的邊連接。結(jié)果如圖所示。
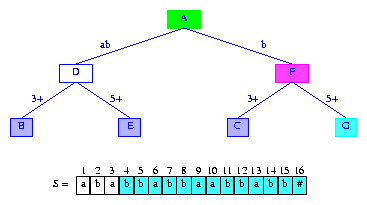
Figure 10 After the insertion of the suffix bbabbaabbabb#
現(xiàn)在我們要為插入后綴suffix(3)時(shí)創(chuàng)建的分支節(jié)點(diǎn)D設(shè)置后綴指針。這個(gè)后綴指針就是新創(chuàng)建的分支節(jié)點(diǎn)F。
節(jié)點(diǎn)F表示的字符串b的最長后綴是空串。因此F的后綴指針指向根結(jié)點(diǎn)。圖11是添加了后綴指針的結(jié)果。
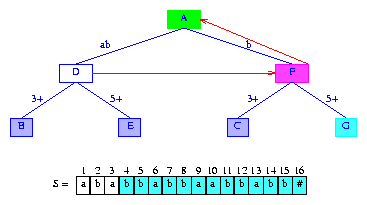
Figure 11 Trie of Figure 10 with suffix pointers added
下一個(gè)要插入的是suffix(5)。由于suffix(5)是剛插入的后綴suffix(4)的最長后綴，我們從活動(dòng)節(jié)點(diǎn)的后綴指針開始。但是當(dāng)前作為活動(dòng)節(jié)點(diǎn)的根結(jié)點(diǎn)沒有后綴指針。因此，活動(dòng)節(jié)點(diǎn)不變。為了保持lastBranchIndex, activeLength, minDistance以及將插入的后綴的索引(5)之間的關(guān)系，需要將minDistance減少1.因此，minDistance變?yōu)?.
因?yàn)閍ctiveLength=0，我們需要從suffix(5)的首字符S[5]開始檢查。活動(dòng)節(jié)點(diǎn)有一條以S[5]=b開始的邊。我們沿著這條邊比較后綴字符和標(biāo)簽字符。由于所有的字符都匹配，我們到達(dá)節(jié)點(diǎn)F。現(xiàn)在F成為活動(dòng)節(jié)點(diǎn)（在檢查后綴字符的過程中，遇到的分支節(jié)點(diǎn)都成為新的活動(dòng)節(jié)點(diǎn)），activeLength=1。我們從當(dāng)前活動(dòng)節(jié)點(diǎn)的某條邊開始繼續(xù)比較。由于下一個(gè)要比較的后綴字符是S[6]=a，我們使用以a開始的邊（如果這樣的邊不存在，新后綴的lastBranchIndex是activeLength+1）。這條邊的標(biāo)簽是3+。當(dāng)比較到新后綴的字符S[10]=a和邊的字符S[7]=b時(shí)，比較結(jié)束。因此，lastBranchIndex(5,5) = 10. minDistance設(shè)置為允許的最大值，也就是lastBranchIndex(5,5) - (index of suffix to be inserted) - activeLength = 10 - 5 - 1 = 4.。
為了插入suffix(5)，我們將節(jié)點(diǎn)F和C之間的邊分裂為二。分裂出現(xiàn)在邊(F,C)的splitDigit=5的字符位置。
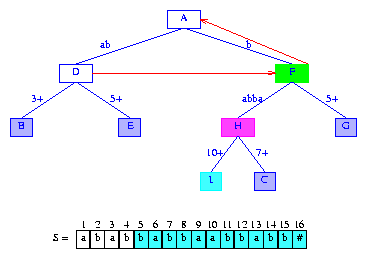
Figure 12 After the insertion of the suffix babbaabbabb#
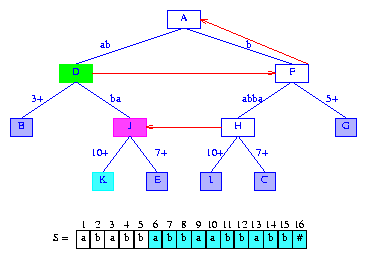
Figure 13 After the insertion of the suffix abbaabbabb#
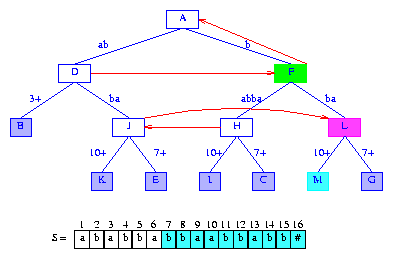
Figure 14 After the insertion of the suffix bbaabbabb#
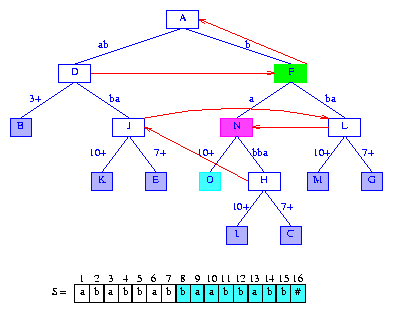
Figure 15 After the insertion of the suffix baabbabb#
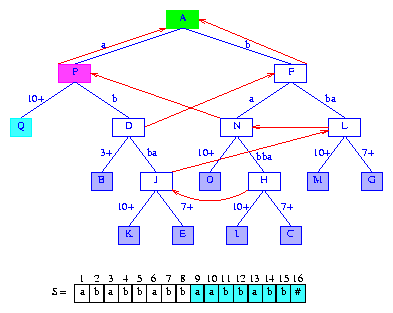
Figure 16 After the insertion of the suffix aabbabb#
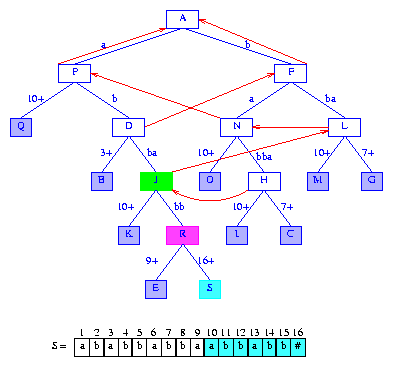
Figure 17 After the insertion of the suffix abbabb#
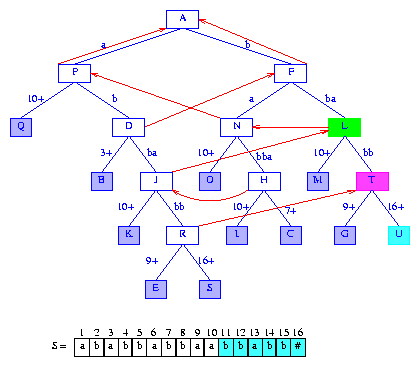
Figure 18 After the insertion of the suffix bbabb#
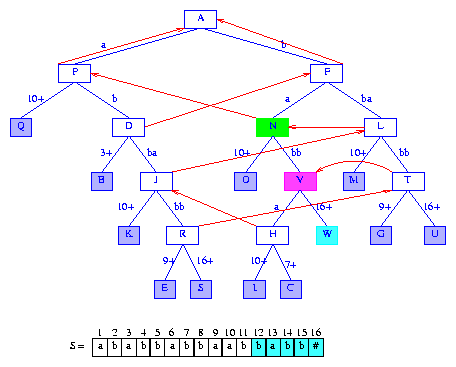
Figure 19 After the insertion of the suffix babb#
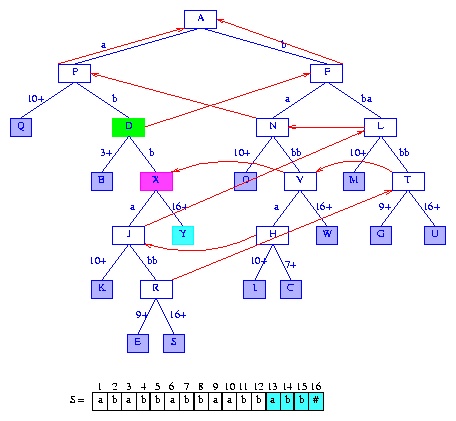
Figure 20 After the insertion of the suffix abb#
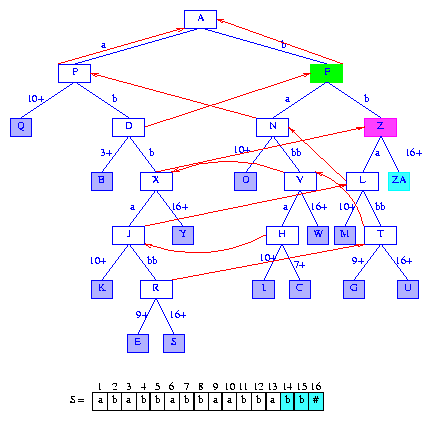
Figure 21 After the insertion of the suffix bb#
復(fù)雜度分析用r表示字符串S的字符集的大小，n表示S的長度（也就是后綴的數(shù)目）。為了插入suffix(i)，我們(a)沿著活動(dòng)節(jié)點(diǎn)的后綴指針（除非活動(dòng)節(jié)點(diǎn)是根結(jié)點(diǎn)）。(b)在已創(chuàng)建的后綴樹中向下移動(dòng)，直到經(jīng)過了minDistance個(gè)字符。(c)然后依次比較后綴和邊的字符，直到確定了lastBranchIndex(i,i)為止。(d)最后插入新的信息節(jié)點(diǎn)和可能的分支節(jié)點(diǎn)。(a)部分消耗的總的時(shí)間是O(n)（一共有n此插入）(b)
部分中，在后綴樹中往下移動(dòng)時(shí)，不需要做比較。每次移動(dòng)到下級(jí)分支節(jié)點(diǎn)需要O(1)時(shí)間。另外，每次移動(dòng)都會(huì)使minDistance減少1.由于開始時(shí)
minDistance為0,并且永遠(yuǎn)不會(huì)小于0,(b)消耗的時(shí)間是O(n + n次插入操作中minDistance增加的總數(shù)). (c)
部分中，確定lastBranchIndex(i,i) 跟 i + activeLength +
minDistance是否相等需要的時(shí)間是O(1)。這只有在minDistance = 0或者位于suffix(i)的activeLength
+ minDistance + 1位置的字符x跟活動(dòng)節(jié)點(diǎn)的合適的邊的minDistance +
1位置的字符不同的時(shí)候才滿足。當(dāng)lastBranchIndex(i,i) != i + activeLength +
minDistance時(shí)，lastBranchIndex(i,i) > i + activeLength +
minDistance，lastBranchIndex(i,i)的值通過對(duì)后綴字符和邊的字符之間做一系列的比較來確定。每進(jìn)行一次這種比
較，minDistance加1.本算法中，只有在這種情景下，minDistance才會(huì)增加。由于minDistance的每次遞增都是S的新的位置
（也就是此位置開始的字符還未比較過的位置）的字符和邊的字符相等的情形的結(jié)果，因此在n次插入中，minDistance增加的總數(shù)是O(n)。每次插入時(shí)，(d)消耗的時(shí)間是O(r)，因?yàn)槲覀冃枰跏蓟獎(jiǎng)?chuàng)建的分支節(jié)點(diǎn)的O(r)個(gè)字段。因此步驟(d)消耗的總的時(shí)間是O(nr)。因此，創(chuàng)建后綴樹消耗的總的時(shí)間是O(nr)。如果假定字符集的大小r是常數(shù)，算法的復(fù)雜度就是O(n)。只有在字符集的大小r很小的情況下，才推薦每個(gè)分支節(jié)點(diǎn)有r個(gè)指向子節(jié)點(diǎn)的字段。當(dāng)字符集很大的時(shí)候（可能會(huì)跟n一樣大，這時(shí)上述算法的復(fù)雜度是O(n^2)），使用哈希表能夠得到O(n)復(fù)雜度的算法。空間復(fù)雜度有O(nr)變?yōu)镺(n)。這里有一個(gè)分治算法實(shí)現(xiàn)的后綴樹，時(shí)間和空間復(fù)雜度都是O(n)（即使字符集的大小是O(n)）。
References and Selected Readings
-
- Department of Energy's Web site for the human genomics project
- Biocomputing Hypertext Coursebook.
Linear
time algorithms to search for a single pattern in a given string can be
found in most algorithm's texts. See, for example, the texts:
- Computer Algorithms, by E. Horowitz, S. Sahni, and S. Rajasekeran, Computer Science Press, New York, 1998.
- Introduction to Algorithms, by T. Cormen, C. Leiserson, and R. Rivest, McGraw-Hill Book Company, New York, 1992.
For more on suffix tree construction, see the papers:
- ``A space economical suffix tree construction algorithm,'' by E. McCreight, Journal of the ACM, 23, 2, 1976, 262-272.
- ``On-line construction of suffix trees,'' by E. Ukkonen, Algorithmica, 14, 3, 1995, 249-260.
- Fast string searching with suffix trees,'' by M. Nelson, Dr. Dobb's Journal, August 1996.
- Optimal suffix tree construction with large alphabets, by M. Farach, IEEE Symposium on the Foundations of Computer Science, 1997.