http://www.cnblogs.com/cgwolver/archive/2009/03/26/1257611.html
假定在右手坐標系中的三角形3點坐標為A,B,C,判斷P是否在ABC之內
( 主要來自 3D引擎研發QQ群(38224573 )的各位朋友的討論 ,我僅僅算做個總結吧,特別感謝各位朋友的熱情支持。 )
方法1:三個Perplane的方法
設AB,BC,AC邊上的垂直平面為Perplane[3],垂直朝向內側的法向為n[3]
1)先根據任意兩邊叉出法向N
N = AB.CrossProduct(AC);
N.Normalize();
D = A.DotProduct( N );
2)如果P在三角形所在平面之外,可直接判定不在平面之內( 假定方程為 ax+by+cz+d = 0 )
if( P.DotProduct( N ) + D > 0 ) return false;
3)然后法向和各邊叉出垂直平面的法向
n[0] = N.CrossProduct(AB); //朝向內側
n[0].Normalize();
Perplane[0].dist = A.DotProduct(n[0]);
Perplane[0].normal = n[0];
同樣方法求得Perplane[1],Perlane[2];
3)因為三個Perplane都朝向三角形內側,P在三角形內的條件是同時在三個Perplane前面;如果給定點P在任意一個垂直平面之后,那么可判定P在三角形外部
for( int i = 0;i<3;j++ )
{
if( P.DotProduct( Perplane[i].normal ) + Perplane[i].dist < 0 )
return false;
}
return true;//如果P沒有在任意一條邊的外面,可判斷定在三角形之內,當然包括在邊上的情況
方法2:三個部分面積與總面積相等的方法
S(PAB) + S(PAC) + S( PBC) = S(ABC) 則判定在三角形之內
用矢量代數方法計算三角形的面積為
S = 1/2*|a|*|b|*sin(theta)
= 1/2*|a|*|b|*sqrt(1-cos^2(theta))
= 1/2*|a|*|b|*sqrt(1- (a.DotProduct(b)/(|a|*|b|))^2);
另一種計算面積的方法是 S = 1/2*|a.CrossProduct(b)|
比較一下,發現后者的精確度和效率都高于前者,因為前者需要開方和求矢量長度,矢量長度相當于一次點乘,三個點乘加一個開方,顯然不如
后者一次叉乘加一次矢量長度(注,一次叉乘計算相當于2次點乘,一次矢量長度計算相當于一次點乘),后者又對又快。
S(ABC) = AB.CrossProduct(AC);//*0.5;
S(PAB) = PA.CrossProduct(PB);//*0.5;
S(PBC) = PB.CrossProduct(PC);//*0.5;
S(PAC) = PC.CrossProduct(PA);//*0.5;
if( S(PAB) + S(PBC) + S(PAC) == S(ABC) )
return true;
return false;
另一種計算三角形面積的矢量方法是 1/2*a.CrossProdcuct(b) ,CrossProduct = ( y1*z2 - y2*z1 , x1*z2 - x2*z1, x1*y2 - x2*z1 )
可以看到CrossProduct 的計算要比DotProduct多3個乘法計算,效率沒有上面的方法高
方法3:三個向量歸一化后相加為0
這個方法很怪異,發現自http://flipcode.spaces.live.com/blog/cns!8e578e7901a88369!903.entry 下面的一個回帖
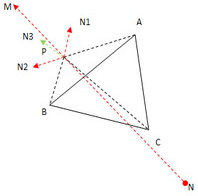
如上圖三角形ABC,P為AB外側一點,N1,N2,N3 分別為BP,AP,CP的歸一化矢量;NM為N1,N2夾角的角平分線
可以看出角A-P-B是三角形內角,必然小于180度,那么角N1-P-N2等于A-P-B;NM是N1-P-N2的角平分線,那么角B-P-N等于角N-P-A,而CPN必然小于其中一個,
即小于180/2 = 90度。結論是角N1,N2的合矢量方向與N3的夾角為銳角。所以N1,N2,N3的合向量模大于1.
這里注意,N3不一定在N1,N2之間,不能假定N2-P-N3 和N3-P-N1這兩個角一定是銳角
同樣可以推導出如果P在三角形內,N1+N2+N3必然小于0;若N1+N2+N3 = 0則P在三角形的邊上。
有沒有更簡單的推導方法?
這個方法看起來很精巧,但是善于優化的朋友會立刻發現,三個矢量歸一化,需要三個開方。迭代式開方太慢了,而快速開方有的時候又不滿足精度要求。
方法4:重心坐標之和為1
{
BaryCenter = ( S(PAB)/S(PABC),S(PBC)/S(PABC),S(PAC)/S(PABC)) // 點P在三角形內的重心坐標
if( BaryCenter.x + BaryCenter.y + BaryCenter.z >0.f )
return false
return true;
}
其中S(PAB),S(ABC),S(PBC),S(PBC) 用上述的方法二種提到的計算三角形面積方法計算。
綜合比較
方法1必須求叉乘,雖然可以通過首先排除不在平面內的點,但是后面仍要求三個叉乘和3個點乘(當然還可排除法優化)
方法2看起來之需要求4個點乘,如果用叉乘方法計算面積,可能會導致效率低下
方法3是看起來是最精巧的方法,但是效率也不能保證...3個開方
方法4和方法2的效率差不多
本文來自CSDN博客,轉載請標明出處:http://blog.csdn.net/boyzk2008/archive/2009/08/07/4421106.aspx