最大m子段和問題：給定由n個整數（可能為負）組成的序列a1、a2、a3...,an,以及一個正整數m，要求確定序列的m個不想交子段，使這m個子段的總和最大！
設b(i,j)表示數組a的前j項中i個子段和的最大值，
并且第i個子段包含a[j](1<=i<=m,i<=j<=n)，則所求的最優值為maxb(m,j)(m<=j<=n)。在這種定義下b(i,j)的遞推公式：b(i,j)=max{b(i,j-1)+a[j],maxb(i-1,t)+a[j](i-1<=t<j)}(1<=i<=m,i<=j<=n)；b(i,j-1)+a[j]表示第i個包含a[j-1]和a[j]，maxb(i-1,t)+a[j]表示第i個子段僅包含a[j]。
這中定義很強悍，尤其是黃色標記部分，直接把b(i,j)把a[j]限制在第i段內，然后再分a[j-1]和a[j]都在子段內和只有a[j]，特殊的當m=1時，b(1,j)=max(b(1,j-1)+a[j],a[j]),1<=j<=n;如果翻譯成文字的話，就是說在數組j位置的最大和子段（包含a[j]）等于數組在j-1位置的最大和子段（包含a(j-1)）加上a[j]和最大和子段只有a[j]的情況的最優值，當然所求解可以表示為maxb(1,j)(1<=j<=n)；
其實如果光從b(1,j)=max(b(1,j-1)+a[j],a[j])這個等式本生出發我們很容易的觀察出b(1,j-1)的正負直接決定著b(1,j)的取值，然后我們可以產生這中想法，如果b(1,j-1)為正，我就繼續加，如果為負我就重新開始加！！！這樣的話，寫成程序就更簡單，其實就是前面我寫的最大子段和的動態規劃方法的解釋。。。（今天終于明白了！！！）
代碼如下：
#include<stdio.h>
int MaxSum1(int m,int n,int *a)//m為切割段數，n為數組大小
{
int i,j,k,sum;
if(n<m||m<1)
return 0;
int **b =new int *[m+1];
for(i=0;i<=m;i++)
b[i]=new int[n+1];
for(i=0;i<=m;i++)
b[i][0]=0;
for(j=1;j<=n;j++)
b[0][j]=0;
for(i=1;i<=m;i++)
for(j=i;j<=n-m+i;j++)
{
if(j>i)
{
b[i][j]=b[i][j-1]+a[j];
for(k=i-1;k<j;k++)
{
if(b[i][j]<b[i-1][k]+a[j])
b[i][j]=b[i-1][k]+a[j];
}
}
else
{
b[i][j]=b[i-1][j-1]+a[j];
}
}
sum=0;
for(j=m;j<=n;j++)
if(sum<b[m][j])
sum=b[m][j];
delete b;
return sum;
}
//教科書上又進行了代碼優化，如下
int MaxSum(int m,int n,int *a)
{
int i,max,j,sum;
if(n<m||m<1)
return 0;
int *b=new int[n+1];
int *c=new int[n+1];
b[0]=0;
c[0]=0;
for(i=1;i<=m;i++)
{
b[i]=b[i-1]+a[i];
c[i-1]=b[i];
max=b[i];
for(j=i+1;j<=i+n-m;j++)
{
b[j]=b[j-1]>c[j-1]?b[j-1]+a[j]:c[j-1]+a[j];
c[j-1]=max;
if(max<b[j])
max=b[j];
}
c[i+n-m]=max;
}
sum=0;
for(j=m;j<=n;j++)
if(sum<b[j])
sum=b[j];
return sum;
}
int main()
{
int n,m;
int a[100],i;
while(scanf("%d %d",&m,&n)!=EOF)
{
for(i=1;i<=n;i++)
scanf("%d",&a[i]);
printf("%d\n",MaxSum(m,n,a));
}
return 0;
} 對于這段代碼我按著思想看了一遍，沒有仔細推敲過，不知道會不會是個禍患，但是測試通過了！！！
posted @
2010-09-11 09:48 jince 閱讀(725) |
評論 (0) |
編輯 收藏
最大和和矩陣是最大和子段的推廣，是最大和子段推廣到二維的形式，當然我們可把二維形再轉化成一維的形式，這就是求最大和矩陣方法了！二維轉化為一維時我們直接用窮舉法！
代碼如下：
#include<stdio.h>
int MaxSum(int n,int *a)
{
int sum=0,b=0;
for(int i=1;i<=n;i++)
{
if(b>0)
b+=a[i];
else
b=a[i];
if(b>sum) sum=b;
}
return sum;
}
int MaxSum2(int m,int n,int a[][100])
{
int sum=0;
int *b=new int [n+1];
for(int i=1;i<=m;i++)
{
for(int k=1;k<=n;k++)
b[k]=0;
for(int j=i;j<=m;j++)
{
for(int k=1;k<=n;k++)
{
b[k]+=a[j][k];
int max=MaxSum(n,b);
if(max>sum)
sum=max;
}
}
}
delete b;
return sum;
}
int main()
{
int a[100][100],i,j,n,sum,m;
while(scanf("%d %d",&m,&n)!=EOF)
{
for(i=1;i<=m;i++)
for(j=1;j<=n;j++)
{
scanf("%d",&a[i][j]);
}
sum=MaxSum2(m,n,a);
printf("%d\n",sum);
}
return 0;
}
運行結果如下：
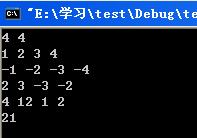
posted @
2010-09-10 13:09 jince 閱讀(540) |
評論 (0) |
編輯 收藏
昨天杭州的天氣真的只能用詭異來形容，上班時，萬里無云！下班時，半邊日出半邊雨！我住在杭城西面，下班是由東往西走的，前面 一個大太陽，后面狂風暴雨，坐在公交車上，時而在雨幕里，時而在夕陽下。。更詭異的是我下來車后就開始打雷了，嚇的我一路狂奔回家，被雨追著跑的感覺真差！狂奔后，才發現自己原來這么虛弱，才跑了1000米左右，就感覺渾身乏力了，在學校體能測試的時候我可是跑第一的，缺少運動呀，看樣子人確實是要常常運動運動，好東西也要常常拾得拾得！
回家后我想起以前我同學問過我的一個問題，為什么是雷聲轟隆隆的？我當時回答是云層碰撞不規整，強度有差異，其實這只是我的猜想。然后我同學又問了，為什么雷聲是轟隆隆傳向遠方，然后消失了！我不知道了，沒做出回答！！當時被同學小小的鄙視了一下，這個問題其實很多中學生都能回答出來！！！今天我又去網上查了一下，雷是怎么產生的，為什么雷聲是轟隆隆的？結果發現了以下文章：
在完成一次閃電的時間內，窄狹的閃電通道上要釋放巨大的電能，因而形成強烈的爆炸，產生沖擊波，然后形成聲波向四周傳開，這就是雷聲或說"打雷"。
聽起來，雷聲可以分為兩種。一種是清脆響亮，象爆炸聲一樣的雷聲，一般叫做"炸雷"；另一種是沉悶的轟隆聲，有人叫它做"悶雷"。還有一種低沉而經久不歇的隆隆聲，有點兒象推磨時發出的聲響。人們常把它叫做"拉磨雷"，實際上是悶雷的一種形式。
閃電通路中的空氣突然劇烈增熱，使它的溫度高達15000-20000℃，因而造成空氣急劇膨脹，通道附近的氣壓可增至一百個大氣壓以上。緊接著，又發生迅速冷卻，空氣很快收縮，壓力減低。這一驟脹驟縮都發生在千分之幾秒的短暫時間內，所以在閃電爆發的一剎那間，會產生沖擊波。沖擊波以5000米/秒的速度向四面八方傳播，在傳播過程中，它的能量很快衰減，而波長則逐漸增長。在閃電發生后0.1-0.3秒，沖擊波就演變成聲波，這就是我們聽見的雷聲。
還有一種說法，認為雷鳴是在高壓電火花的作用下，由于空氣和水汽分子分解而形成的爆炸瓦斯發生爆炸時所產生的聲音。雷鳴的聲音在最初的十分之幾秒時間內，跟爆炸聲波相同。這種爆炸波擴散的速度約為5000米／秒，在之后0.1-0.3秒鐘，它就演變為普通聲波。
人們常說的炸雷，一般是距觀測者很近的云對地閃電所發出的聲音。在這種情況下，觀測者在見到閃電之后，幾乎立即就聽到雷聲；有時甚至在閃電同時即聽見雷聲。因為閃電就在觀測者附近，它所產生的爆炸波還來不及演變成普通聲波，所以聽起來猶如爆炸聲一般。
如果云中閃電時，雷聲在云里面多次反射，在爆炸波分解時，又產生許多頻率不同的聲波，它們互相干擾，使人們聽起來感到聲音沉悶，這就是我們聽到的悶雷。一般說來，悶雷的響度比炸雷來得小，也沒有炸雷那么嚇人。
拉磨雷是長時間的悶雷。雷聲拖長的原因主要是聲波在云內的多次反射以及遠近高低不同的多次閃電所產生的效果。此外聲波遇到山峰、建筑物或地面時，也產生反射。有的聲波要經過多次反射。這多次反射有可能在很短的時間間隔內先后傳入我們的耳朵。這時，我們聽起來，就覺得雷聲沉悶而悠長，有如拉磨之感。
黃色標注部分為雷聲轟隆隆的原因，解釋的挺容易讓人接受的，我現在回憶昨天看到的閃電和聽到的雷聲，好像是聲波不斷反射傳入我耳朵里的結果，最后聲波慢慢消失，就聽不到了！
現在我又回想了下當時同學問問題時候場景，如果當時能夠從我現在的角度出發，結合到動態規劃知識，就可能會回答出問題了。。。首先，最優子結構為聲源發出聲波傳入我耳朵里（這個很明顯能知道）；然后聲波遇到障礙物反射（其實可以看做新的聲源），再次傳入我的耳朵，不過音量會變小（這個過程和最優子結構性質是相同，當然能夠想到這一步才能回答出同學問題，但是從最優子結構是可以猜想后來雷聲轟隆隆的）；最后就有不同的反射聲波傳入我的耳朵，聽到轟隆隆混雜的聲音！
可惜沒有如果，不過我現在知道了也好，雖然我同學當時沒有告訴我原因，但是他告訴我怎么測聲源的位置，聲音的速度是340米每秒，從閃電發光的時候，開始數秒設為t，340*t就是數秒人與聲源的距離了（解釋是聲速與光速差太多了，所以光傳入眼睛的時間可以看做是聲源發出聲音的時間，這也是為什么打雷的時候先看到閃電，后聽到雷聲的原因）。
解釋了這些，我還有一點不清楚，就是經常聽見飛機在天上飛，但是一抬頭飛機卻在另一個地方！！！
posted @
2010-09-10 11:25 jince 閱讀(1889) |
評論 (0) |
編輯 收藏
摘要: 均分紙牌
Time Limit:1000MS Memory Limit:65536KTotal Submit:241 Accepted:103
Description
有 N 堆紙牌，編號分別為 1，2，…, N。每堆上有若干張，但紙牌總數必為 N 的倍數。可以在任一堆上取若干張紙牌，然后移動。移牌規則為：在編號為 1 堆上取的紙牌，只能移到編號為 2 的堆上；在...
閱讀全文
posted @
2010-09-09 13:00 jince 閱讀(2972) |
評論 (2) |
編輯 收藏
弄了一個早上的最接近點對，沒弄明白。。。還是做點簡單的吧！
代碼如下：
#include<stdio.h>
#include<stdlib.h>
#include<time.h>
#include<iostream>
using namespace std;
int main()
{
int magic,i;
srand(time(NULL));//srand()需包含頭文件stdlib.h，種子！
printf("RAND_MAX=%d\n",RAND_MAX);//原來RAND_MAX是個常量32767；rand()函數的返回值范圍：0~32767
for(i=1;i<10;i++)//輸出十個1~100隨機數
{
magic=rand()/(int)(((unsigned)RAND_MAX+1)/100);
// magic=rand()%100+1;//課堂上老師說這樣可以取1~100之間的隨機數，今天才明白原來是跟100取余的結果！
printf("%d ",magic);
}
printf("\n");
double a[10];
for(i=0;i<10;i++)
a[i]=(double)rand()/RAND_MAX;//這樣寫可以變成小數！
for(i=0;i<10;i++)
printf("%.2lf ",a[i]);
printf("\n");
return 0;
}
posted @
2010-09-08 12:43 jince 閱讀(408) |
評論 (2) |
編輯 收藏
簡單的問題串聯可以組成復雜！
給定已經排好序的n個元素a[0...n-1]，現在在這n個元素中找出一特定元素x。
代碼如下：
#include<stdio.h>
#include<iostream>
#include<algorithm>
using namespace std;
template <class Type>
int BinarySearch(Type a[],Type& x,int n)
{
int left=0;
int right=n-1;
while(left<=right)
{
int middle=(left+right)/2;
if(x==a[middle])
return middle;
if(x>middle)
left=middle+1;
else
right=middle-1;
}
return -1;
}
template <class Type> //重載
int BinarySearch(Type a[],Type& x,int left,int right)
{
int middle=(left+right)/2;
if(x==a[middle])
return middle;
else if(x>middle)
return BinarySearch(a,x,middle+1,right);
else
return BinarySearch(a,x,left,middle-1);
return -1;
}
int main()
{
int i,n,x;
int a[100];
while(scanf("%d",&n)!=EOF)
{
for(i=0;i<n;i++)
scanf("%d",&a[i]);
sort(a,a+n);
for(i=0;i<n;i++)
printf("%d ",a[i]);
printf("\n");
scanf("%d",&x);
printf("%d\n",BinarySearch(a,x,n));
printf("%d\n",BinarySearch(a,x,0,n-1));
}
return 0;
}
運行結果：
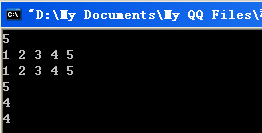
posted @
2010-09-07 22:42 jince 閱讀(225) |
評論 (0) |
編輯 收藏
我們不斷做著把事情翻譯成語言的工作！
漢諾塔老生常談的問題！
個人體會：一、理解函數意義和數據意義！
二、想象力，就像把一棵二叉樹先展開，再收攏！
直接上代碼（注釋以前寫的）：
#include<stdio.h>
int count1,count;//count1,表示第一個圓盤移動的次數
//count，表示總的移動次數
/**//*函數功能：限制移動過程
函數參數： 整形變量num，表示第n個盤子
自發性變量 from，表示源木樁
字符型變量to，表示目的木樁
*/
void move(int num,char from,char to)
{
printf("move %d:from %c to %c\n",num,from,to);
count++;
}
/**//*函數功能：將第n個盤子從源木樁A，借助于木樁C移動到木樁B
函數參數：n，表示第n個盤子
a，表示源木樁a
b，表示目的木樁b
c，表示過度木樁c*/
/**//*我自己想法：
三個木樁，從第n個盤開始移動，只有當其他的盤都在c木樁才能移動n，
同理要將第n-1個盤從c移動到b，要將n-2個盤全部移動到a木樁*/
void hanoi(int n,char a,char b,char c)
{
if(n==1) //遞歸出口：為什么是n==1?
{
move(n,a,b); //第n個盤子由a->b
count1++;
}
else
{
hanoi(n-1,a,c,b); //將第n-1個盤子，借助于b由a->c
move(n,a,b); //第n個盤子有a->b
hanoi(n-1,c,b,a); //將第n-1個盤子，借助于a有c->b
}
}
int main()
{
int n;
while(n!=0)
{
scanf("%d",&n);
hanoi(n,'A','B','C');
printf("count=%d\n",count);
printf("count1=%d\n",count1);
}
return 0;
}
/**//*通過程序運行，我們還可以得到：
當n為偶數時，第一個盤第一次移動移動到c，
當n為奇數時，第一個盤第一次移動到移動到b*/
運行結果：
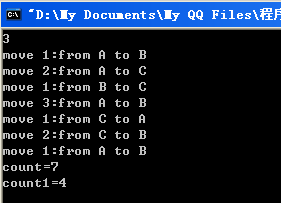
posted @
2010-09-07 21:56 jince 閱讀(243) |
評論 (0) |
編輯 收藏
有n=2^k個運動員比賽，現要求設計一張比賽日程表，要求如下：
(1)每個選手必須與其他n-1個選手各比賽一次；
(2)每個選手一天只能比賽一次；
(3)循環賽一共進行n-1天；
這個題目自己列下表，觀察一下規律就成，書上說的二分不是那么好理解！重在實際應用。。。
代碼如下：
#include<stdio.h>
void Table(int k,int a[][100])
{
int n=1;
int i,j,s,t;
for(i=1;i<=k;i++)
n*=2;
for(i=1;i<=n;i++)
a[1][i]=i;
int m=1;
for(s=1;s<=k;s++)
{
n/=2;
for(t=1;t<=n;t++)
for(i=m+1;i<=2*m;i++)
for(j=m+1;j<=2*m;j++)
{
a[i][j+(t-1)*m*2]=a[i-m][j+(t-1)*m*2-m];
a[i][j+(t-1)*m*2-m]=a[i-m][j+(t-1)*m*2];
}
m*=2;
}
}
int main()
{
int a[100][100];
Table(3,a);
int i,j;
for(i=1;i<=8;i++)
{
for(j=1;j<=8;j++)
printf("%d ",a[i][j]);
printf("\n");
}
return 0;
}
結果：
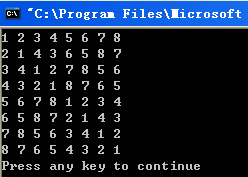
posted @
2010-09-07 20:53 jince 閱讀(256) |
評論 (0) |
編輯 收藏 最大公約的兩種求法：
代碼如下：
#include<stdio.h>
int gcds(int a,int b)//stein算法
{
if(a<b){
int temp = a;
a = b;
b=temp;
}
if(0==b) //b=0返回
return a;
if(a%2==0 && b%2 ==0) //a和b都是偶數
return 2*gcds(a/2,b/2);
if ( a%2 == 0) // a是偶數，b是奇數
return gcds(a/2,b);
if ( b%2==0 ) // a是奇數，b是偶數
return gcds(a,b/2);
return gcds((a+b)/2,(a-b)/2);// a和b都是奇數
}
int gcdo(int a,int b) //歐幾里得
{
if(b==0)
return a;
if(a<b){
int temp = a;
a = b;
b=temp;
}
return gcdo(b,a%b);
}
int main()
{
int a,b;
while(scanf("%d %d",&a,&b)!=EOF)
{
printf("%d\n%d\n",gcds(a,b),gcdo(a,b));
}
return 0;
}
歐幾里得算法，當初老師給我們的時候，只是說這樣求可以求得最大公約數，沒給出證明。。
百度上搜了一下，基本證明思想a，b(a>b)的公約數和a，a%b的公約數是相同的。Stein算法證明也類似！！
posted @
2010-09-07 12:09 jince 閱讀(778) |
評論 (0) |
編輯 收藏
苦惱啊！
Description
設有n個正整數，將他們連接成一排，組成一個最大的多位整數。例如:n=3時，3個整數13,312,343,連成的最大整數為:34331213
又如:n=4時,4個整數7,13,4,246連接成的最大整數為7424613
Input
N
N個數
Output
連接成的多位數
Sample Input
3
13 312 343
0
Sample Output
34331213
這個題目意思應該很好理解，至少會想有兩種解題思路，
一、把數組從大到小排列，這樣是最大嗎？ 顯然不是，例如：123 9，應該輸出9123；
二、把數組按字符串排序，這樣是最大嗎？這問題可能會然我們困惑，但是這也是錯的，例如：120，12；應該輸出12120；
這個題目不知道毒害了多少人（當然我指的是ACM新人），尤其是第二種思路去寫代碼的。。這只是一個悲劇的開始，你把一條彎路在直走！
其實這個題目應該是屬于動態規劃的最簡單應用！子問題，給你兩個數，讓你連成最大數，一定非常簡單，只能組成兩個數，比較一下大小就成！這就是解題思路！
如果給你三個數呢？一直遞推下去！悲劇啊，盡然怎么簡單！
代碼如下：
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
int main()
{
int n,i,j,l,k;
char s[1000][100];
char s1[200],s2[200];
while(scanf("%d",&n)!=EOF&&n!=0)
{
for(i=0;i<n;i++)
{
scanf("%s",s[i]);
while(s[i][0]=='0')
{
if(strlen(s[i])==1)
break;
strcpy(s[i],s[i]+1);
}
}
for(i=0;i<n;i++)
{
for(j=i+1;j<n;j++)
{
strcpy(s1,s[i]);
strcat(s1,s[j]);
strcpy(s2,s[j]);
strcat(s2,s[i]);
if(strcmp(s1,s2)<0)
{
strcpy(s1,s[i]);
strcpy(s[i],s[j]);
strcpy(s[j],s1);
}
}
}
for(i=0;i<n;i++)
{
if(s[0][0]=='0')
{
printf("0");
break;
}
else
{
printf("%s",s[i]);
}
}
printf("\n");
}
return 0;
}
本來我也是第二種思路的，我看了感覺不像，因為以前寫過了！
早上的幾點收獲：
1、<string>頭文件和<string.h>頭文件是不一樣的！運行時的一個錯誤，弄了一個早上，最后發現這什么個問題！
2、運用容器，排序字符串
vector<string> words;
string str;
while(scanf("%s",str)!=EOF)
words.push_back(str);
sort(words.begin(),words.end(),greater<string>());
for(vector<string>::size_type i=0;i<words.size();i++)
{
cout<<words[i]<<endl;
}
不過會有很多警告，讓我很苦惱！有誰知道呢？
警告如下：
--------------------Configuration: rongqi - Win32 Debug--------------------
Compiling
rongqi.cpp
c:\documents and settings\administrator\桌面\rongqi\rongqi.cpp(81) : warning C4786: 'std::reverse_iterator<std::basic_string<char,std::char_traits<char>,std::allocator<char> > const *,std::basic_string<char,std::char_traits<char>,std::allocator<char
> >,std::basic_string<char,std::char_traits<char>,std::allocator<char> > const &,std::basic_string<char,std::char_traits<char>,std::allocator<char> > const *,int>' : identifier was truncated to '255' characters in the debug information
c:\documents and settings\administrator\桌面\rongqi\rongqi.cpp(81) : warning C4786: 'std::reverse_iterator<std::basic_string<char,std::char_traits<char>,std::allocator<char> > *,std::basic_string<char,std::char_traits<char>,std::allocator<char> >,st
d::basic_string<char,std::char_traits<char>,std::allocator<char> > &,std::basic_string<char,std::char_traits<char>,std::allocator<char> > *,int>' : identifier was truncated to '255' characters in the debug information
c:\program files\microsoft visual studio\vc98\include\vector(39) : warning C4786: 'std::vector<std::basic_string<char,std::char_traits<char>,std::allocator<char> >,std::allocator<std::basic_string<char,std::char_traits<char>,std::allocator<char> > >
>::vector<std::basic_string<char,std::char_traits<char>,std::allocator<char> >,std::allocator<std::basic_string<char,std::char_traits<char>,std::allocator<char> > > >' : identifier was truncated to '255' characters in the debug information
c:\program files\microsoft visual studio\vc98\include\vector(60) : warning C4786: 'std::vector<std::basic_string<char,std::char_traits<char>,std::allocator<char> >,std::allocator<std::basic_string<char,std::char_traits<char>,std::allocator<char> > >
>::~vector<std::basic_string<char,std::char_traits<char>,std::allocator<char> >,std::allocator<std::basic_string<char,std::char_traits<char>,std::allocator<char> > > >' : identifier was truncated to '255' characters in the debug information
rongqi.obj - 0 error(s), 0 warning(s)
3、在程序頭上寫#pragma warning (disable: 4786)，可以注銷4786以后警告！
posted @
2010-09-06 11:52 jince 閱讀(908) |
評論 (0) |
編輯 收藏