| |
常用鏈接
留言簿(4)
隨筆分類
隨筆檔案
搜索
最新評(píng)論
閱讀排行榜
評(píng)論排行榜
Powered by: 博客園
模板提供：滬江博客
|
|
|
|
|
發(fā)新文章 |
|
 |
給定a,b,設(shè)G=gcd(a,b),于是有a=A*G,b=B*G(1<=A,B,gcd(A,B)=1) 對(duì)于a的多次加可以看成K*a(1<=k),轉(zhuǎn)化成(K*a)%b的所有結(jié)果能否表示成0..b-1中的所有數(shù), 假(K*a)%b=M,M=K*a-W*b(W為使M>0的最大整數(shù)),M=K*A*G-W*B*G M%G==0, 既結(jié)果是G的倍數(shù),如果想取得0..b-1中的所有數(shù)， 那么必須G=1才可能.. 這算法牛X。。。
 #include"stdio.h"
int main()
   {
 long m,n,k,i;
while(scanf("%ld%ld",&m,&n)!=-1)
  { printf("%10ld%10ld ",m,n);
k=1;
for(i=2;i<=(m>n?n:m);i++)
{
if(m%i==0&&n%i==0)
k=i;
 }
if(k==1)
printf("Good Choice\n\n");
else
printf("Bad Choice\n\n");
}
 }
媽的，沒見過那么惡心的題目。。。 首先題目就錯(cuò)了，1不是質(zhì)數(shù)啊！！！ 輸出之間居然還有一空行。。。 檢查了半天都沒查出來，殺人了！！！ 懶得改了，用了同學(xué)的
#include <iostream>
#include <vector>
#include <string>
#include <math.h>
#include <iomanip>
#include <stdlib.h>
using namespace std;
#include"stdio.h"
#include"math.h"
int p[2001];
int main()
{
int n,c,n1;
int i,j;
int tol;
int flag;
while(scanf("%d%d",&n,&c)!=-1)
{
p[1]=1;
tol=1;
for(i=2;i<=3000;i++)
{
flag=1;
for(j=2;j<=(int)sqrt((double)i);j++)
{
if(i%j==0){flag=0;break;}
}
if(flag==0)continue;
else if(i>n)break;
else
{
tol++;
p[tol]=i;
}
}
//此時(shí)質(zhì)數(shù)的個(gè)數(shù)是tol,第一個(gè)質(zhì)數(shù)是1
printf("%d %d:",n,c);
if(tol%2==0&&tol>=c*2)
{
for(i=1;i<=c*2;i++)
{
j=(tol-c*2)/2;
printf(" %d",p[j+i]);
}
printf("\n\n");
}
if(tol%2==0&&tol<c*2)
{
for(j=1;j<=tol;j++)
printf(" %d",p[j]);
printf("\n\n");
}
if(tol%2==1&&tol>=c*2-1)
{
for(i=1;i<=c*2-1;i++)
{
j=(tol-c*2+1)/2;
printf(" %d",p[i+j]);
}
printf("\n\n");
}
if(tol%2==1&&tol<c*2-1)
{
for(j=1;j<=tol;j++)
{
printf(" %d",p[j]);
}
printf("\n\n");
}
}
}
傳說中的動(dòng)態(tài)規(guī)劃。。。 注意題目的優(yōu)先計(jì)算順序。先是考慮是否會(huì)小于0，然后才考慮是否會(huì)大于20，要不然就會(huì)WA。 哇塞,真的這樣,這題太假了。。。
#include <iostream>
#include <vector>
#include <string>
#include <math.h>
#include <iomanip>
#include <stdlib.h>
using namespace std;
int w[21][21][21];
void init()
{
for (int i=0;i<21;i++)
{
for (int j=0;j<21;j++)
{
for (int k=0;k<21;k++)
{
if(i==0||j==0||k==0)
w[i][j][k]=1;
else if(i<j&&j<k)
w[i][j][k]=w[i][j][k-1]+w[i][j-1][k-1]-w[i][j-1][k];
else
w[i][j][k]=w[i-1][j][k]+w[i-1][j-1][k]+w[i-1][j][k-1]-w[i-1][j-1][k-1];
}
}
}
}
int main()
{
init();
int a,b,c;
while (scanf("%d %d %d",&a,&b,&c)!=EOF)
{
if (a==-1&&b==-1&&c==-1)
{break;
}
if (a<=0||b<=0||c<=0)
{
printf("w(%d, %d, %d) = %d\n",a,b,c,w[0][0][0]);
}
else if (a>20||b>20||c>20)
{
printf("w(%d, %d, %d) = %d\n",a,b,c,w[20][20][20]);
}
else
{
printf("w(%d, %d, %d) = %d\n",a,b,c,w[a][b][c]);
}
}
}
Trie樹就是字典樹，其核心思想就是空間換時(shí)間。
舉個(gè)簡(jiǎn)單的例子。
給你100000個(gè)長(zhǎng)度不超過10的單詞。對(duì)于每一個(gè)單詞，我們要判斷他出沒出現(xiàn)過，如果出現(xiàn)了，第一次出現(xiàn)第幾個(gè)位置。
這題當(dāng)然可以用hash來，但是我要介紹的是trie樹。在某些方面它的用途更大。比如說對(duì)于某一個(gè)單詞，我要詢問它的前綴是否出現(xiàn)過。這樣hash就不好搞了，而用trie還是很簡(jiǎn)單。
現(xiàn)在回到例子中，如果我們用最傻的方法，對(duì)于每一個(gè)單詞，我們都要去查找它前面的單詞中是否有它。那么這個(gè)算法的復(fù)雜度就是O(n^2)。顯然對(duì)于100000的范圍難以接受。現(xiàn)在我們換個(gè)思路想。假設(shè)我要查詢的單詞是abcd，那么在他前面的單詞中，以b，c，d，f之類開頭的我顯然不必考慮。而只要找以a開頭的中是否存在abcd就可以了。同樣的，在以a開頭中的單詞中，我們只要考慮以b作為第二個(gè)字母的……這樣一個(gè)樹的模型就漸漸清晰了……
假設(shè)有b，abc，abd，bcd，abcd，efg，hii這6個(gè)單詞，我們構(gòu)建的樹就是這樣的。
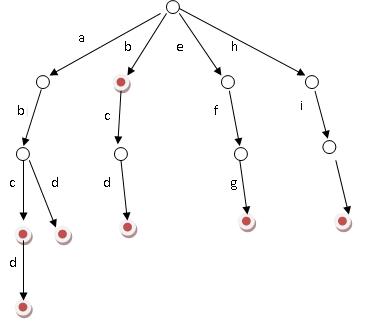
對(duì)于每一個(gè)節(jié)點(diǎn)，從根遍歷到他的過程就是一個(gè)單詞，如果這個(gè)節(jié)點(diǎn)被標(biāo)記為紅色，就表示這個(gè)單詞存在，否則不存在。
那么，對(duì)于一個(gè)單詞，我只要順著他從跟走到對(duì)應(yīng)的節(jié)點(diǎn)，再看這個(gè)節(jié)點(diǎn)是否被標(biāo)記為紅色就可以知道它是否出現(xiàn)過了。把這個(gè)節(jié)點(diǎn)標(biāo)記為紅色，就相當(dāng)于插入了這個(gè)單詞。
這樣一來我們?cè)儐柡筒迦肟梢砸黄鹜瓿桑脮r(shí)間僅僅為單詞長(zhǎng)度，在這一個(gè)樣例，便是10。
我們可以看到，trie樹每一層的節(jié)點(diǎn)數(shù)是26^i級(jí)別的。所以為了節(jié)省空間。我們用動(dòng)態(tài)鏈表，或者用數(shù)組來模擬動(dòng)態(tài)。空間的花費(fèi)，不會(huì)超過單詞數(shù)×單詞長(zhǎng)度。
給出一個(gè)用類封裝的字典樹代碼，厄。。。做ACM的模板用另一個(gè)。。應(yīng)該放在了“ACM模板”文件夾下了。。。
#include <cstdio>
#include <iostream>
#include <cstring>
using namespace std;
const int num_chars = 26;
class Trie {
public:
Trie():root(NULL){};
Trie(Trie& tr);
int search(const char* word, char* entry ) const;
int insert(const char* word, const char* entry);
int remove(const char* word, char* entry);
private:
struct Trie_node
{
char* data;
Trie_node* branch[num_chars];
Trie_node();
}* root;
};
Trie::Trie_node::Trie_node()
{
data = NULL;
for (int i=0; i<num_chars; ++i)
branch[i] = NULL;
}
int Trie::search(const char* word, char* entry ) const
{
int position = 0;
char char_code;
Trie_node *location = root;
while( location!=NULL && *word!=0 )
{
if (*word>='A' && *word<='Z')
char_code = *word-'A';
else if (*word>='a' && *word<='z')
char_code = *word-'a';
else return 0;
location = location->branch[char_code];
position++;
word++;
}
if ( location != NULL && location->data != NULL )
{
strcpy(entry,location->data);
return 1;
}
else return 0;
}
int Trie::insert(const char* word, const char* entry)
{
int result = 1, position = 0;
if ( root == NULL ) root = new Trie_node;
char char_code;
Trie_node *location = root;
while( location!=NULL && *word!=0 )
{
if (*word>='A' && *word<='Z')
char_code = *word-'A';
else if (*word>='a' && *word<='z')
char_code = *word-'a';
else return 0;
if( location->branch[char_code] == NULL )
location->branch[char_code] = new Trie_node;
location = location->branch[char_code];
position++;
word++;
}
if (location->data != NULL)
result = 0;
else {
location->data = new char[strlen(entry)+1];
strcpy(location->data, entry);
}
return result;
}
int main()
{
Trie t;
char entry[100];
t.insert("aa", "DET");
t.insert("abacus","NOUN");
t.insert("abalone","NOUN");
t.insert("abandon","VERB");
t.insert("abandoned","ADJ");
t.insert("abashed","ADJ");
t.insert("abate","VERB");
t.insert("this", "PRON");
if (t.search("this", entry))
cout<<"'this' was found. pos: "<<entry<<endl;
if (t.search("abate", entry))
cout<<"'abate' is found. pos: "<<entry<<endl;
if (t.search("baby", entry))
cout<<"'baby' is found. pos: "<<entry<<endl;
else
cout<<"'baby' does not exist at all!"<<endl;
if (t.search("aa", entry))
cout<<"'aa was found. pos: "<<entry<<endl;
}
PS:實(shí)現(xiàn)方法 http://met.fzu.edu.cn/eduonline/web/web/resources/articleContent.asp?id=346
摘要: 今天總算是碰到一道復(fù)雜題了。。。（我BT了？）弄死我了，主要是排除重復(fù)情況，我想不通，最后參考了前人的代碼，修改后AC了。。。思路：通過遞歸，得出可能存在的解法，并記錄，查找原記錄，若存在相同則取消記錄
#include <iostream>#include <vector>#include <string>#include&nb... 閱讀全文
<本文中排序都是采用的從小到大排序>
一、對(duì)int類型數(shù)組排序
程序代碼 程序代碼
int num[100];
Sample:
int cmp ( const void *a , const void *b )
{
return *(int *)a - *(int *)b;
}
qsort(num,100,sizeof(num[0]),cmp);
二、對(duì)char類型數(shù)組排序（同int類型）
程序代碼 程序代碼
char word[100];
Sample:
int cmp( const void *a , const void *b )
{
return *(char *)a - *(char*)b;
}
qsort(word,100,sizeof(word[0]),cmp)
三、對(duì)double類型數(shù)組排序（特別要注意）
程序代碼 程序代碼
double in[100];
int cmp( const void *a , const void *b )
{
return *(double *)a > *(double *)b ? 1 : -1;
} qsort(in,100,sizeof(in[0]),cmp)；
四、對(duì)結(jié)構(gòu)體一級(jí)排序
程序代碼 程序代碼
struct In {
double data;
int other;
}s[100]
//按照data的值從小到大將結(jié)構(gòu)體排序,關(guān)于結(jié)構(gòu)體內(nèi)的排序關(guān)鍵數(shù)據(jù)data的類型可以很多種，
參考上面的例子寫
int cmp( const void *a ,const void *b)
{
return (*(In *)a).data > (*(In *)b).data ? 1 : -1;
}
qsort(s,100,sizeof(s[0]),cmp);
五、對(duì)結(jié)構(gòu)體二級(jí)排序
程序代碼 程序代碼
struct In {
int x; int y;
}s[100];
//按照x從小到大排序，當(dāng)x相等時(shí)按照y從大到小排序
int cmp( const void *a , const void *b )
{
struct In *c = (In *)a;
struct In *d = (In *)b;
if(c->x != d->x) return c->x - d->x;
else return d->y - c->y;
}
qsort(s,100,sizeof(s[0]),cmp);
六、對(duì)字符串進(jìn)行排序
程序代碼 程序代碼
struct In {
int data; char str[100];
}s[100];
//按照結(jié)構(gòu)體中字符串str的字典順序排序
int cmp ( const void *a , const void *b )
{
return strcmp( (*(In *)a)->str , (*(In *)b)->str );
}
qsort(s,100,sizeof(s[0]),cmp);
七、計(jì)算幾何中求凸包的cmp
程序代碼 程序代碼
int cmp(const void *a,const void *b)
//重點(diǎn)cmp函數(shù)，把除了1點(diǎn)外的所有點(diǎn)，旋轉(zhuǎn)角度排序
{
struct point *c=(point *)a;
struct point *d=(point *)b;
if( calc(*c,*d,p[1]) < 0) return 1;
else if( !calc(*c,*d,p[1])
&& dis(c->x,c->y,p[1].x,p[1].y) < dis(d->x,d->y,p[1].x,p[1].y))
//如果在一條直線上，則把遠(yuǎn)的放在前面
return 1; else return -1;
}
PS: 其中的qsort函數(shù)包含在<stdlib.h>的頭文件里，strcmp包含在<string.h>的頭文件里
|
|