題意是一個(gè)覆蓋問題,用n個(gè)各種邊長(zhǎng)的小三角形來覆蓋一個(gè)六邊形,基本上可以直接深搜,可以試著覆蓋六分之一,三分之一和二分之一至全部,四種覆蓋形式有一種達(dá)到完全覆蓋即可退出,以此來降低復(fù)雜度。
對(duì)三角形坐標(biāo)的表示上采用了如下的表示法:
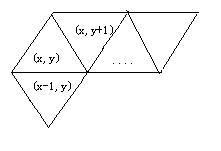
以這種方式來表示整個(gè)六邊形上的三角形(圖畫的比較省略。。因?yàn)槲抑粫?huì)用畫圖。。。。)
這題主要的難點(diǎn)不在思路,而在coding
 #include<iostream>
#include<iostream>
 #include<cstring>
#include<cstring>
 using namespace std;
using namespace std;
 int l,n;
int l,n;
 int t[10];
int t[10];
 bool b[60][110];
bool b[60][110];
 bool used[26];
bool used[26];
 bool square_vis[6*25*25+1];
bool square_vis[6*25*25+1];
 int zero;
int zero;
 struct node
struct node


 {
{
 int x;
int x;
 int y;
int y;
 } stack[1000];
} stack[1000];
 void flood_line(int x,int y,int l,int c)
void flood_line(int x,int y,int l,int c)


 {
{
 int i,j;
int i,j;
 int tx,ty;
int tx,ty;
 if ((x+y)%2)
if ((x+y)%2)


 {
{
 i = l-1;
i = l-1;
 for (j=y-i; j<=y+i; j++)
for (j=y-i; j<=y+i; j++)
 b[x+i][j] = c;
b[x+i][j] = c;
 }
}
 else
else


 {
{
 i = l-1;
i = l-1;
 tx = x+i;
tx = x+i;
 ty = y+i;
ty = y+i;
 for (j=0; j<2*i+1; j++)
for (j=0; j<2*i+1; j++)


 {
{
 b[tx][ty] = c;
b[tx][ty] = c;
 if (j%2)ty++;
if (j%2)ty++;
 else tx--;
else tx--;
 }
}
 }
}
 }
}
 void flood(int x,int y,int l,int c)
void flood(int x,int y,int l,int c)


 {
{
 if ((x+y)%2)
if ((x+y)%2)


 {
{
 for (int i=0; i<l; i++)
for (int i=0; i<l; i++)
 for (int j=y-i; j<=y+i; j++)
for (int j=y-i; j<=y+i; j++)
 b[x+i][j] = c;
b[x+i][j] = c;
 }
}
 else
else


 {
{
 for (int i =0; i<l; i++)
for (int i =0; i<l; i++)


 {
{
 int tx = x+i;
int tx = x+i;
 int ty = y+i;
int ty = y+i;
 for (int j=0; j<2*i+1; j++)
for (int j=0; j<2*i+1; j++)


 {
{
 b[tx][ty] = c;
b[tx][ty] = c;
 if(j%2)
if(j%2)
 ty++;
ty++;
 else tx--;
else tx--;
 }
}
 }
}
 }
}
 }
}
 int cal(int x,int y)
int cal(int x,int y)


 {
{
 int tx,ty,i,j;
int tx,ty,i,j;
 if ((x+y)%2)
if ((x+y)%2)


 {
{
 for (i=0; ; i++)
for (i=0; ; i++)
 for (j=y-i; j<=y+i; j++)
for (j=y-i; j<=y+i; j++)
 if(b[x+i][j])
if(b[x+i][j])
 return i;
return i;
 }
}
 else
else


 {
{
 for (i=0; ; i++)
for (i=0; ; i++)


 {
{
 tx = x+i;
tx = x+i;
 ty = y+i;
ty = y+i;
 for (j=0; j<2*i+1; j++)
for (j=0; j<2*i+1; j++)


 {
{
 if (b[tx][ty])
if (b[tx][ty])
 return i;
return i;
 if (j%2)
if (j%2)
 ty++;
ty++;
 else tx--;
else tx--;
 }
}
 }
}
 }
}
 }
}
 bool search(int step)
bool search(int step)


 {
{
 int x,y;
int x,y;
 int i,maxl;
int i,maxl;
 x = stack[step-1].x;
x = stack[step-1].x;
 y = stack[step-1].y;
y = stack[step-1].y;

 while(x<2*l)
while(x<2*l)


 {
{
 if (b[x][y]) y++;
if (b[x][y]) y++;
 else break;
else break;
 if (y>100)
if (y>100)


 {
{
 x++; y=0;
x++; y=0;
 }
}
 }
}
 if (x>=2*l)
if (x>=2*l)
 return true;
return true;
 maxl = cal(x,y);
maxl = cal(x,y);
 flood(x,y,maxl,1);
flood(x,y,maxl,1);
 zero -= maxl*maxl;
zero -= maxl*maxl;
 stack[step].x= x;
stack[step].x= x;
 stack[step].y = y;
stack[step].y = y;

 for (i=maxl; i>=2; i--)
for (i=maxl; i>=2; i--)


 {
{
 if(used[i]&&square_vis[zero]&&search(step+1))
if(used[i]&&square_vis[zero]&&search(step+1))
 return true;
return true;
 flood_line(x,y,i,0);
flood_line(x,y,i,0);
 zero+=(2*i-1);
zero+=(2*i-1);
 }
}
 b[x][y] = 0;
b[x][y] = 0;
 zero++;
zero++;
 return false;
return false;
 }
}
 void init()
void init()


 {
{
 memset(used,false,sizeof(used));
memset(used,false,sizeof(used));
 cin >> l;
cin >> l;
 cin >> n;
cin >> n;
 for (int i=0; i<n; i++)
for (int i=0; i<n; i++)


 {
{
 cin >> t[i];
cin >> t[i];
 used[t[i]] = true;
used[t[i]] = true;
 }
}
 n = 0;
n = 0;
 for (int i=1; i<=l; i++)
for (int i=1; i<=l; i++)
 if (used[i])
if (used[i])
 t[n++] = i;
t[n++] = i;
 }
}
 void run()
void run()


 {
{
 for(int i=0; i<n; i++)
for(int i=0; i<n; i++)
 if(l%t[i]==0)
if(l%t[i]==0)


 {
{
 cout << "YES"<<endl;
cout << "YES"<<endl;
 return;
return;
 }
}
 bool length_vis[26];
bool length_vis[26];
 memset(length_vis,false,sizeof(length_vis));
memset(length_vis,false,sizeof(length_vis));
 length_vis[0] = true;
length_vis[0] = true;
 for (int i = 0; i<=l; i++)
for (int i = 0; i<=l; i++)
 if (length_vis[i])
if (length_vis[i])
 for (int j=0; j<n; j++)
for (int j=0; j<n; j++)
 if (i+t[j]<=l)
if (i+t[j]<=l)
 length_vis[i+t[j]] = true;
length_vis[i+t[j]] = true;
 if (!length_vis[l])
if (!length_vis[l])


 {
{
 cout << "NO"<<endl;
cout << "NO"<<endl;
 return;
return;
 }
}
 memset(square_vis,false,sizeof(square_vis));
memset(square_vis,false,sizeof(square_vis));
 square_vis[0] = true;
square_vis[0] = true;
 for (int i=0; i<=6*l*l; i++)
for (int i=0; i<=6*l*l; i++)
 if (square_vis[i])
if (square_vis[i])
 for (int j=0; j<n; j++)
for (int j=0; j<n; j++)
 if (i+t[j]*t[j]<=6*l*l)
if (i+t[j]*t[j]<=6*l*l)
 square_vis[i+t[j]*t[j]]= true;
square_vis[i+t[j]*t[j]]= true;
 if (!square_vis[6*l*l])
if (!square_vis[6*l*l])


 {
{
 cout << "NO"<<endl;
cout << "NO"<<endl;
 return;
return;
 }
}
 memset(b,true,sizeof(b));
memset(b,true,sizeof(b));
 flood(0,25,l,0);
flood(0,25,l,0);
 zero = l*l;
zero = l*l;
 stack[0].x = 0;
stack[0].x = 0;
 stack[0].y = 25;
stack[0].y = 25;
 if (search(1))
if (search(1))


 {
{
 cout << "YES"<<endl;
cout << "YES"<<endl;
 return;
return;
 }
}
 memset(b,true,sizeof(b));
memset(b,true,sizeof(b));
 flood(0,25,l,0);
flood(0,25,l,0);
 flood(0,26,l,0);
flood(0,26,l,0);
 zero = l*l*2;
zero = l*l*2;
 if (search(1))
if (search(1))


 {
{
 cout<< "YES"<<endl;
cout<< "YES"<<endl;
 return;
return;
 }
}
 memset(b,true,sizeof(b));
memset(b,true,sizeof(b));
 flood(0,25,l,0);
flood(0,25,l,0);
 flood(0,26,l,0);
flood(0,26,l,0);
 flood(0,25+2*l,l,0);
flood(0,25+2*l,l,0);
 zero = l*l*3;
zero = l*l*3;
 if (search(1))
if (search(1))


 {
{
 cout << "YES"<<endl;
cout << "YES"<<endl;
 return;
return;
 }
}
 memset(b,true,sizeof(b));
memset(b,true,sizeof(b));
 flood(0,25,l,0);
flood(0,25,l,0);
 flood(0,26,l,0);
flood(0,26,l,0);
 flood(0,25+2*l,l,0);
flood(0,25+2*l,l,0);
 flood(l,25-l+1,l,0);
flood(l,25-l+1,l,0);
 flood(l,25+l,l,0);
flood(l,25+l,l,0);
 flood(l,25+l+1,l,0);
flood(l,25+l+1,l,0);
 zero = 6*l*l;
zero = 6*l*l;
 if (search(1))
if (search(1))


 {
{
 cout << "YES"<<endl;
cout << "YES"<<endl;
 return;
return;
 }
}
 cout << "NO"<<endl;
cout << "NO"<<endl;
 return;
return;
 }
}
 int main()
int main()


 {
{
 int cas;
int cas;
 cin >> cas;
cin >> cas;
 while(cas--)
while(cas--)


 {
{
 init();
init();
 run();
run();
 }
}
 }
}