幾天不寫程序手就有點(diǎn)生，整理了一段把圖片轉(zhuǎn)成ASCII碼的程序。暫時只支持24位真彩色圖片，ASCII碼可以自行擴(kuò)充。大體算法就是把整個位圖分成8*16的小塊，計(jì)算小塊的灰度值總和，然后匹配一個灰度值接近的字符。具體算法細(xì)節(jié)可以參考網(wǎng)上資料。
程序源代碼可以在
這里下載。
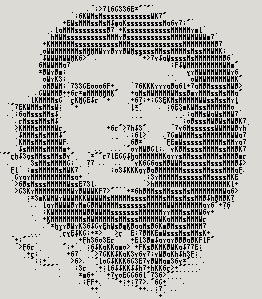
posted @
2008-06-29 18:03 小四 閱讀(4008) |
評論 (11) |
編輯 收藏打算做一個開源的矢量繪圖軟件(類似MS Visio)，花了幾天把程序框架做了出來，自認(rèn)比DrawCLI的稍微好一點(diǎn)點(diǎn)。支持基本圖形繪制，旋轉(zhuǎn)，縮放，串行化。使用MFC、STL、GDI/GDI+和一點(diǎn)點(diǎn)設(shè)計(jì)模式。
自知做一個堪用的矢量繪圖軟件是個非常艱巨的事情，不過還是打算用一些業(yè)余時間把這件事情做了，對自己以往掌握的知識，也是一個總結(jié)。
編譯好的可執(zhí)行程序程序0.01版本源代碼在
這里可以下載
posted @
2008-01-29 18:16 小四 閱讀(12265) |
評論 (37) |
編輯 收藏The barrier to change is not too little caring; it is too much complexity.
To turn caring into action, we need to see a problem, see a solution, and see the impact. But complexity blocks all three steps.
If we can really see a problem, which is the first step, we come to the second step: cutting through the complexity to find a solution.
Cutting through complexity to find a solution runs through four predictable stages: determine a goal, find the highest-leverage approach, discover the ideal technology for that approach, and in the meantime, make the smartest application of the technology that you already have — whether it's something sophisticated, like a drug, or something simpler, like a bednet.
The final step – after seeing the problem and finding an approach – is to measure the impact of your work and share your successes and failures so that others learn from your efforts.
But if you want to inspire people to participate, you have to show more than numbers; you have to convey the human impact of the work – so people can feel what saving a life means to the families affected.
posted @
2008-01-15 10:04 小四 閱讀(369) |
評論 (0) |
編輯 收藏GDI+的顏色矩陣由一個5*5的float型數(shù)組構(gòu)成，用來對每一個像素的顏色(R,G,B,A)做線性變換，每個像素顏色與矩陣相乘。把一幅彩色圖轉(zhuǎn)成灰度圖的算法是，假設(shè)像素點(diǎn)顏色為(r,g,b)，轉(zhuǎn)換成灰度圖三個顏色分量是一樣的，稱作灰階，灰階的計(jì)算是 r*0.299+g*0.587+b*0.114。我們可以逐個像素轉(zhuǎn)換，也可以使用顏色矩陣。所以彩色圖轉(zhuǎn)灰度圖的顏色矩陣為
ColorMatrix matrix =
{0.299, 0.299, 0.299, 0, 0,
0.587, 0.587, 0.587, 0, 0,
0.114, 0.114, 0.114, 0, 0,
0, 0, 0, 1, 0,
0, 0, 0, 0, 0}
這樣轉(zhuǎn)換后，灰度圖的灰階分布在0~255之間。如果想把一幅彩色圖渲染成雙色圖，定義一個深顏色darker，一個淺顏色lighter,那么灰度圖只是一個darker是黑色而lighter是白色的特例。本來分布在0~255的灰階，這樣應(yīng)該分別分布在(lighter.r~darker.r),(lighter.g~darker.g),(lighter.b~darker.b)。
編寫代碼如下，使用白色和紫色。
void CDuotoneDlg::OnButton1()
{
Bitmap img(L"c:\\test1.jpg");
Graphics graphix(this->GetDC()->m_hDC);
Color darker(0);
Color lighter(8414370);
const float gray_r = 0.299f;
const float gray_g = 0.587f;
const float gray_b = 0.114f;
float offset_r = (float)darker.GetR() / 255;
float offset_g = (float)darker.GetG() / 255;
float offset_b = (float)darker.GetB() / 255;
float r = (float)(lighter.GetR() - darker.GetR()) / 255;
float g = (float)(lighter.GetG() - darker.GetG()) / 255;
float b = (float)(lighter.GetB() - darker.GetB()) / 255;
ImageAttributes imgatt;
ColorMatrix matrix =
{
gray_r*r, gray_r*g, gray_r*b, 0, 0,
gray_g*r, gray_g*g, gray_g*b, 0, 0,
gray_b*r, gray_b*g, gray_b*b, 0, 0,
0, 0, 0, 1, 0,
offset_r, offset_g, offset_b, 0, 1
};
imgatt.SetColorMatrix(&matrix, ColorMatrixFlagsDefault, ColorAdjustTypeBitmap);
int iWidth = img.GetWidth();
int iHeight = img.GetHeight();
graphix.DrawImage(
&img,
Rect(0, 0, iWidth, iHeight),
0.0f,
0.0f,
iWidth,
iHeight,
UnitPixel,
&imgatt);
graphix.ReleaseHDC(this->GetDC()->m_hDC);
}
渲染圖片測試
posted @
2008-01-05 14:01 小四 閱讀(679) |
評論 (0) |
編輯 收藏
摘要: 表達(dá)式求值的關(guān)鍵點(diǎn)在于中綴表達(dá)式轉(zhuǎn)后綴表達(dá)式，算法書上都有明確介紹就不多說了。動手實(shí)現(xiàn)了一個表達(dá)式解析器，支持括號、多位整數(shù)以及表達(dá)式合法性判斷。今天的狀態(tài)實(shí)在很差，本想對表達(dá)式進(jìn)行合法性判斷的時候使用一些類似哈希表的技巧，比如使用一個大的bool數(shù)組，合法字符ASC碼對應(yīng)的項(xiàng)設(shè)置為1，比如可以直接判斷CHARS['+']是否為true,省去查找的時間。后來發(fā)現(xiàn)一共就支持那幾個字符，這樣做未免有點(diǎn)...
閱讀全文
posted @
2008-01-04 19:59 小四 閱讀(718) |
評論 (0) |
編輯 收藏二叉排序樹，又稱二叉查找樹，左子樹結(jié)點(diǎn)值一律小于父結(jié)點(diǎn)，右子樹結(jié)點(diǎn)值一律大于父結(jié)點(diǎn)，查找平均算法復(fù)雜度為O(logn)。
還是那道統(tǒng)計(jì)單詞數(shù)目的題目，使用二叉排序樹來解決，查找和插入以及統(tǒng)計(jì)數(shù)目使用一個函數(shù)解決，比使用哈希表的優(yōu)勢在于，中序遍歷輸出結(jié)果，單詞是有序的。
程序中需要注意的地方，釋放樹結(jié)點(diǎn)的時候，要使用后續(xù)遍歷，先釋放子結(jié)點(diǎn)后才釋放根結(jié)點(diǎn)。
/**//* -------------------------------------------------------------------------
// 文件名 ： binarytree.h
// 創(chuàng)建者 ： dj
// 創(chuàng)建時間 ： 2008-1-1
// 功能描述 ： 二叉排序樹
// -----------------------------------------------------------------------*/
#ifndef __BINARYTREE_H__
#define __BINARYTREE_H__
#define SAFE_DELETE(p) {if(p) { delete [] (p); (p) = NULL;}}
struct TreeNode
{
TreeNode(const char* s):
counter(1), left(NULL), right(NULL)
{
name = new char[strlen(s)+1];
strcpy(name, s);
}
~TreeNode()
{
SAFE_DELETE(name);
}
char* name;
int counter;
TreeNode* left;
TreeNode* right;
};
class BinaryTree
{
public:
BinaryTree():m_pRoot(NULL)
{}
~BinaryTree()
{
FreeTree(m_pRoot);
}
void Lookup(const char* sName)
{
TreeNode** p = &m_pRoot;
while(*p)
{
int cmp = strcmp(sName, (*p)->name);
if (cmp<0)
p = &((*p)->left);
else if (cmp>0)
p = &((*p)->right);
else //found the word
{
((*p)->counter)++; //increase the counter
return;
}
}
// not found, then add the word node.
TreeNode* pNode = new TreeNode(sName);
*p = pNode;
}
void Dump(const char* sFile)
{
ofstream f(sFile);
Travel(m_pRoot, f);
f.close();
}
private:
void Travel(TreeNode* pNode, ofstream& f)
{
if (!pNode)
return;
Travel(pNode->left, f);
f<<pNode->name<<" "<<pNode->counter<<endl;
Travel(pNode->right, f);
}
void FreeTree(TreeNode* pNode)
{
if(!pNode)
return;
FreeTree(pNode->left);
FreeTree(pNode->right);
delete pNode;
}
private:
TreeNode* m_pRoot;
};
#endif //__BINARYTREE_H__
int main(int argc, char* argv[])
{
BinaryTree tree;
ifstream f("c:\\ip.txt");
string s;
while(f>>s)
{
tree.Lookup(s.c_str());
}
tree.Dump("c:\\stat.txt");
return 0;
}
posted @
2008-01-01 21:49 小四 閱讀(443) |
評論 (0) |
編輯 收藏
折半查找又叫二分查找，要求查找表本身必須是有序的。查找算法復(fù)雜度為O(logn)。C標(biāo)準(zhǔn)庫提供折半查找的庫函數(shù)，聲明如下
bsearch(const void *, const void *, size_t, size_t, int (__cdecl *)(const void *, const void *));
最后一個參數(shù)要求一個指向比較函數(shù)的指針。程序設(shè)計(jì)實(shí)踐上寫道，為bsearch提供一個key就這么費(fèi)勁，寫一個好的通用的排序程序也不容易，即使這樣，使用bsearch而不是自己另外寫仍然是個好主意。
多年的歷史證明，程序員能把二分檢索程序?qū)懻_也是很不容易的(Over the years, binary search has proven surprisingly hard for programmer to get right)。
于是自己用模板寫一個折半查找函數(shù)，寫好一個十幾行的程序，也不是看上去那么簡單的事情。
template<typename T>
int binarysearch(const T* tab, int ntab, const T& value)
{
int low = 0;
int high = ntab;
while(low <= high)
{
int mid = (low+high)/2;
if(value<tab[mid])
high = mid - 1;
else if (value>tab[mid])
low = mid + 1;
else
return mid;
}
return -1;
}
測試程序
int main(int argc, char* argv[])
{
int a[] = {2, 4, 6, 7, 8, 9, 13};
int aa = sizeof(a);
int n = binarysearch(a, sizeof(a)/sizeof(a[0]), 4);
cout<<n<<endl;
return 0;
}
posted @
2008-01-01 17:59 小四 閱讀(1101) |
評論 (0) |
編輯 收藏
摘要: 寫了一個哈希表模板類，用于統(tǒng)計(jì)一篇文章中不同單詞出現(xiàn)的次數(shù)。哈希表使用char*作為key,使用桶式鏈表指針數(shù)組(指向結(jié)點(diǎn)鏈表的指針數(shù)組)來索引，字符串哈希函數(shù)是在網(wǎng)上搜來的。模板參數(shù)一個是值類型，另一個NBARREL是指針數(shù)組的大小，通常是越大哈希值沖突就越少，結(jié)點(diǎn)鏈表長度也就越短，當(dāng)然查找就越快。
為了方便統(tǒng)計(jì)，為哈希表增加了一個IncValue函數(shù)，提高效率。統(tǒng)計(jì)的時候使用了快速排序，為了...
閱讀全文
posted @
2007-12-30 15:13 小四 閱讀(569) |
評論 (0) |
編輯 收藏在程序設(shè)計(jì)實(shí)踐上看到這個簡單的快速排序，用模板重新寫了一遍，加深一下印象。平均算法復(fù)雜度為O(nlogn)。
其中尋找支點(diǎn)元素pivot有多種方法，不同的方法會導(dǎo)致快速排序的不同性能。根據(jù)分治法平衡子問題的思想，希望支點(diǎn)元素可以使p[m..n]盡量平均地分為兩部分，但實(shí)際上很難做到。下面給出幾種尋找pivot的方法。
1.選擇p[m..n]的第一個元素p[m]的值作為pivot；
2.選擇p[m..n]的最后一個元素p[n]的值作為pivot；
3.選擇p[m..n]中間位置的元素p[k]的值作為pivot；
4.選擇p[m..n]的某一個隨機(jī)位置上的值p[random(n-m)+m]的值作為pivot；
按照第4種方法隨機(jī)選擇pivot的快速排序法又稱隨機(jī)化版本的快速排序法，在實(shí)際應(yīng)用中該方法的性能也是最好的。本程序使用第4種方法。要求節(jié)點(diǎn)類型支持比較運(yùn)算符。
template<typename T>
void quicksort(T* v, int n)
{
if (n<=1)
return;
int last = 0;
int pivot = rand()%n;
swap(v, 0, pivot);
for (int i = 1; i < n; i++)
{
if (v[i]<v[0])
swap(v, ++last, i);
}
swap(v, last, 0);
quicksort(v, last);
quicksort(v+last+1, n-last-1);
}
template<typename T>
void swap(T* v, int i, int j)
{
T tmp = v[i];
v[i] = v[j];
v[j] = tmp;
}
隨手寫一個不太好看的測試程序
struct str
{
str(const char* a)
{
assert(a);
v = new char[strlen(a)+1];
strcpy(v, a);
}
str(const str& a)
{
assert(a.v);
v = new char[strlen(a.v)+1];
strcpy(v, a.v);
}
~str()
{
delete [] v;
}
void operator = (const str& a)
{
if (this == &a)
return;
assert(a.v);
delete [] v;
v = new char[strlen(a.v)+1];
strcpy(v, a.v);
}
bool operator == (const str& a) const
{
return (strcmp(v, a.v)==0);
}
bool operator > (const str& a) const
{
return (strcmp(v, a.v)>0);
}
bool operator < (const str& a) const
{
return (strcmp(v, a.v)<0);
}
char* v;
};
int main(int argc, char* argv[])
{
int* array = new int [10];
for(int i = 0; i < 10; i++)
array[i] = rand();
quicksort(array, 10);
for(i = 0; i < 10; i++)
{
cout<<array[i]<<endl;
}
str s[] = {"bd", "e", "ba", "a"};
quicksort(s, 4);
for(i = 0; i < 4; i++)
{
cout<<s[i].v<<endl;
}
return 0;
}
posted @
2007-12-29 14:31 小四 閱讀(430) |
評論 (0) |
編輯 收藏復(fù)習(xí)一下數(shù)據(jù)結(jié)構(gòu)，用鏈表實(shí)現(xiàn)了一個堆棧模板類。
寫的過程中用到一些知識點(diǎn)，碰到一些問題，隨手記下來。
1：mystack<int> s; mystack<int> s2 = s;
編譯器會把s2 = s編譯成拷貝構(gòu)造函數(shù)s2(s)，此時調(diào)用的是拷貝構(gòu)造函數(shù)，而不是賦值函數(shù)(切記)。
另外有時候編譯器這種自做聰明，自動調(diào)用符合參數(shù)類型的構(gòu)造函數(shù)會帶來很難發(fā)現(xiàn)的錯誤，為了防止編譯器這么做，可以在構(gòu)造函數(shù)聲明前加explicit關(guān)鍵字。
2：不改變成員變量值的函數(shù)，例如empty()，要聲明為const,這點(diǎn)很重要，不然當(dāng)一個const mystack&類型的對象調(diào)用empty()的時候，會編不過。
3：拷貝構(gòu)造函數(shù)最好要先判斷是否是拷貝自身，不然有時候就出錯。
4：拷貝構(gòu)造函數(shù)也別忘了成員變量初始化列表。
template<typename T>
class mystack
{
public:
mystack();
mystack(const mystack& src);
~mystack();
bool push(const T& data);
T pop();
bool empty() const;
void clear();
mystack& operator = (const mystack& src);
private:
void copystack(mystack& dst, const mystack& src);
struct stacknode
{
T data;
stacknode* pnext;
};
stacknode* phead;
};
template<typename T>
mystack<T>::mystack():phead(NULL)
{}
template<typename T>
mystack<T>::mystack(const mystack<T>& src):
phead(NULL)
{
copystack(*this, src);
}
template<typename T>
mystack<T>::~mystack()
{
clear();
}
template<typename T>
void mystack<T>::clear()
{
while(!empty())
{
pop();
}
}
template<typename T>
void mystack<T>::copystack(mystack& dst, const mystack& src)
{
stacknode* p = src.phead;
mystack<T> tmp;
while(p)
{
tmp.push(p->data);
p = p->pnext;
}
while(!tmp.empty())
{
dst.push(tmp.pop());
}
}
template<typename T>
mystack<T>& mystack<T>::operator=(const mystack& src)
{
if (this == &src)
return *this;
clear();
copystack(*this, src);
return *this;
}
template<typename T>
bool mystack<T>::empty() const
{
return(phead == NULL);
}
template<typename T>
bool mystack<T>::push(const T& data)
{
stacknode* p = new stacknode;
if (!p) return false;
p->data = data;
p->pnext = phead;
phead = p;
return true;
}
template<typename T>
T mystack<T>::pop()
{
assert(!empty());
T data;
data = phead->data;
stacknode* tmp = phead;
phead = phead->pnext;
delete tmp;
return data;
}
int main(int argc, char* argv[])
{
mystack<int> s;
for (int i = 0; i < 1000; i++)
s.push(rand());
mystack<int> s2(s);
while(!s2.empty())
{
cout<<s2.pop()<<endl;
}
return 0;
}
posted @
2007-12-27 13:15 小四 閱讀(413) |
評論 (1) |
編輯 收藏