#
高斯消元法,是線性代數(shù)中的一個(gè)算法,可用來(lái)求解線性方程組,并可以求出矩陣的秩,以及求出可逆方陣的逆矩陣。
高斯消元法的原理是:
若用初等行變換將增廣矩陣 化為 ,則AX = B與CX = D是同解方程組。
所以我們可以用初等行變換把增廣矩陣轉(zhuǎn)換為行階梯陣,然后回代求出方程的解。
以上是線性代數(shù)課的回顧,下面來(lái)說(shuō)說(shuō)高斯消元法在編程中的應(yīng)用。
首先,先介紹程序中高斯消元法的步驟:
(我們?cè)O(shè)方程組中方程的個(gè)數(shù)為equ,變?cè)膫€(gè)數(shù)為var,注意:一般情況下是n個(gè)方程,n個(gè)變?cè)怯行╊}目就故意讓方程數(shù)與變?cè)獢?shù)不同)
1. 把方程組轉(zhuǎn)換成增廣矩陣。
2. 利用初等行變換來(lái)把增廣矩陣轉(zhuǎn)換成行階梯陣。
枚舉k從0到equ – 1,當(dāng)前處理的列為col(初始為0) ,每次找第k行以下(包括第k行),col列中元素絕對(duì)值最大的列與第k行交換。如果col列中的元素全為0,那么則處理col + 1列,k不變。
3. 轉(zhuǎn)換為行階梯陣,判斷解的情況。
① 無(wú)解
當(dāng)方程中出現(xiàn)(0, 0, …, 0, a)的形式,且a != 0時(shí),說(shuō)明是無(wú)解的。
② 唯一解
條件是k = equ,即行階梯陣形成了嚴(yán)格的上三角陣。利用回代逐一求出解集。
③ 無(wú)窮解。
條件是k < equ,即不能形成嚴(yán)格的上三角形,自由變?cè)膫€(gè)數(shù)即為equ – k,但有些題目要求判斷哪些變?cè)遣蝗倍ǖ摹?br> 這里單獨(dú)介紹下這種解法:
首先,自由變?cè)衯ar - k個(gè),即不確定的變?cè)辽儆衯ar - k個(gè)。我們先把所有的變?cè)暈椴淮_定的。在每個(gè)方程中判斷不確定變?cè)膫€(gè)數(shù),如果大于1個(gè),則該方程無(wú)法求解。如果只有1個(gè)變?cè)敲丛撟冊(cè)纯汕蟪觯礊榇_定變?cè)?br>
以上介紹的是求解整數(shù)線性方程組的求法,復(fù)雜度是O(n3)。浮點(diǎn)數(shù)線性方程組的求法類似,但是要在判斷是否為0時(shí),加入EPS,以消除精度問(wèn)題。
下面講解幾道OJ上的高斯消元法求解線性方程組的題目:
POJ 1222 EXTENDED LIGHTS OUT
http://acm.pku.edu.cn/JudgeOnline/problem?id=1222
POJ 1681 Painter's Problem
http://acm.pku.edu.cn/JudgeOnline/problem?id=1681
POJ 1753 Flip Game
http://acm.pku.edu.cn/JudgeOnline/problem?id=1753
POJ 1830 開(kāi)關(guān)問(wèn)題
http://acm.pku.edu.cn/JudgeOnline/problem?id=1830
POJ 3185 The Water Bowls
http://acm.pku.edu.cn/JudgeOnline/problem?id=3185
開(kāi)關(guān)窗戶,開(kāi)關(guān)燈問(wèn)題,很典型的求解線性方程組的問(wèn)題。方程數(shù)和變量數(shù)均為行數(shù)*列數(shù),直接套模板求解即可。但是,當(dāng)出現(xiàn)無(wú)窮解時(shí),需要枚舉解的情況,因?yàn)闊o(wú)法判斷哪種解是題目要求最優(yōu)的。
POJ 2947 Widget Factory
http://acm.pku.edu.cn/JudgeOnline/problem?id=2947
求解同余方程組問(wèn)題。與一般求解線性方程組的問(wèn)題類似,只要在求解過(guò)程中加入取余即可。
注意:當(dāng)方程組唯一解時(shí),求解過(guò)程中要保證解在[3, 9]之間。
POJ 1166 The Clocks
http://acm.pku.edu.cn/JudgeOnline/problem?id=1166
經(jīng)典的BFS問(wèn)題,有各種解法,也可以用逆矩陣進(jìn)行矩陣相乘。
但是這道題用高斯消元法解決好像有些問(wèn)題(困擾了我N天...持續(xù)困擾中...),由于周期4不是素?cái)?shù),故在求解過(guò)程中不能進(jìn)行取余(因?yàn)槿∮嗫赡軐?dǎo)致解集變大),但最后求解集時(shí),還是需要進(jìn)行取余操作,那么就不能保證最后求出的解是正確的...在discuss里提問(wèn)了好幾天也沒(méi)人回答...希望哪位路過(guò)的大牛指點(diǎn)下~~
POJ 2065 SETI
http://acm.pku.edu.cn/JudgeOnline/problem?id=2065
同樣是求解同余方程組問(wèn)題,由于題目中的p是素?cái)?shù),可以直接在求解時(shí)取余,套用模板求解即可。(雖然AC的人很少,但它還是比較水的一道題,)
POJ 1487 Single-Player Games
http://acm.pku.edu.cn/JudgeOnline/problem?id=1487
很麻煩的一道題目...題目中的敘述貌似用到了編譯原理中的詞法定義(看了就給人不想做的感覺(jué)...)
解方程組的思想還是很好看出來(lái)了(前提是通讀題目不下5遍...),但如果把樹的字符串表達(dá)式轉(zhuǎn)換成方程組是個(gè)難點(diǎn),我是用棧 + 遞歸的做法分解的。首先用棧的思想求出該結(jié)點(diǎn)的孩子數(shù),然后遞歸分別求解各個(gè)孩子。
這題解方程組也與眾不同...首先是求解浮點(diǎn)數(shù)方程組,要注意精度問(wèn)題,然后又詢問(wèn)不確定的變?cè)辞懊嬲f(shuō)的方法求解。
一頓折騰后,這題居然寫了6000+B...而且囧的是巨人C++ WA,G++ AC,可能還是精度的問(wèn)題吧...看這題目,看這代碼,就沒(méi)有改的欲望...
hdu OJ 2449
http://acm.hdu.edu.cn/showproblem.php?pid=2449
哈爾濱現(xiàn)場(chǎng)賽的一道純高斯題,當(dāng)時(shí)鶴牛敲了1個(gè)多小時(shí)...主要就是寫一個(gè)分?jǐn)?shù)類,套個(gè)高精模板(偷懶點(diǎn)就Java...)搞定~~
注意下0和負(fù)數(shù)時(shí)的輸出即可。
fze OJ 1704
http://acm.fzu.edu.cn/problem.php?pid=1704
福大月賽的一道題目,還是經(jīng)典的開(kāi)關(guān)問(wèn)題,但是方程數(shù)和變?cè)獢?shù)不同(考驗(yàn)?zāi)0宓臅r(shí)候到了~~),最后要求增廣陣的階,要用到高精度~~
Sgu 275 To xor or not to xor
http://acm.sgu.ru/problem.php?contest=0&problem=275
題解:
http://hi.baidu.com/czyuan%5Facm/blog/item/be3403d32549633d970a16ee.html
這里提供下自己寫的還算滿意的求解整數(shù)線性方程組的模板(浮點(diǎn)數(shù)類似,就不提供了)~~
/* 用于求整數(shù)解得方程組. */
#include <iostream>
#include <string>
#include <cmath>
using namespace std;
const int maxn = 105;
int equ, var; // 有equ個(gè)方程,var個(gè)變?cè)T鰪V陣行數(shù)為equ, 分別為0到equ - 1,列數(shù)為var + 1,分別為0到var.
int a[maxn][maxn];
int x[maxn]; // 解集.
bool free_x[maxn]; // 判斷是否是不確定的變?cè)?
int free_num;
void Debug(void)
{
int i, j;
for (i = 0; i < equ; i++)
{
for (j = 0; j < var + 1; j++)
{
cout << a[i][j] << " ";
}
cout << endl;
}
cout << endl;
}
inline int gcd(int a, int b)
{
int t;
while (b != 0)
{
t = b;
b = a % b;
a = t;
}
return a;
}
inline int lcm(int a, int b)
{
return a * b / gcd(a, b);
}
// 高斯消元法解方程組(Gauss-Jordan elimination).(-2表示有浮點(diǎn)數(shù)解,但無(wú)整數(shù)解,-1表示無(wú)解,0表示唯一解,大于0表示無(wú)窮解,并返回自由變?cè)膫€(gè)數(shù))
int Gauss(void)
{
int i, j, k;
int max_r; // 當(dāng)前這列絕對(duì)值最大的行.
int col; // 當(dāng)前處理的列.
int ta, tb;
int LCM;
int temp;
int free_x_num;
int free_index;
// 轉(zhuǎn)換為階梯陣.
col = 0; // 當(dāng)前處理的列.
for (k = 0; k < equ && col < var; k++, col++)
{ // 枚舉當(dāng)前處理的行.
// 找到該col列元素絕對(duì)值最大的那行與第k行交換.(為了在除法時(shí)減小誤差)
max_r = k;
for (i = k + 1; i < equ; i++)
{
if (abs(a[i][col]) > abs(a[max_r][col])) max_r = i;
}
if (max_r != k)
{ // 與第k行交換.
for (j = k; j < var + 1; j++) swap(a[k][j], a[max_r][j]);
}
if (a[k][col] == 0)
{ // 說(shuō)明該col列第k行以下全是0了,則處理當(dāng)前行的下一列.
k--; continue;
}
for (i = k + 1; i < equ; i++)
{ // 枚舉要?jiǎng)h去的行.
if (a[i][col] != 0)
{
LCM = lcm(abs(a[i][col]), abs(a[k][col]));
ta = LCM / abs(a[i][col]), tb = LCM / abs(a[k][col]);
if (a[i][col] * a[k][col] < 0) tb = -tb; // 異號(hào)的情況是兩個(gè)數(shù)相加.
for (j = col; j < var + 1; j++)
{
a[i][j] = a[i][j] * ta - a[k][j] * tb;
}
}
}
}
Debug();
// 1. 無(wú)解的情況: 化簡(jiǎn)的增廣陣中存在(0, 0, ..., a)這樣的行(a != 0).
for (i = k; i < equ; i++)
{ // 對(duì)于無(wú)窮解來(lái)說(shuō),如果要判斷哪些是自由變?cè)敲闯醯刃凶儞Q中的交換就會(huì)影響,則要記錄交換.
if (a[i][col] != 0) return -1;
}
// 2. 無(wú)窮解的情況: 在var * (var + 1)的增廣陣中出現(xiàn)(0, 0, ..., 0)這樣的行,即說(shuō)明沒(méi)有形成嚴(yán)格的上三角陣.
// 且出現(xiàn)的行數(shù)即為自由變?cè)膫€(gè)數(shù).
if (k < var)
{
// 首先,自由變?cè)衯ar - k個(gè),即不確定的變?cè)辽儆衯ar - k個(gè).
for (i = k - 1; i >= 0; i--)
{
// 第i行一定不會(huì)是(0, 0, ..., 0)的情況,因?yàn)檫@樣的行是在第k行到第equ行.
// 同樣,第i行一定不會(huì)是(0, 0, ..., a), a != 0的情況,這樣的無(wú)解的.
free_x_num = 0; // 用于判斷該行中的不確定的變?cè)膫€(gè)數(shù),如果超過(guò)1個(gè),則無(wú)法求解,它們?nèi)匀粸椴淮_定的變?cè)?
for (j = 0; j < var; j++)
{
if (a[i][j] != 0 && free_x[j]) free_x_num++, free_index = j;
}
if (free_x_num > 1) continue; // 無(wú)法求解出確定的變?cè)?
// 說(shuō)明就只有一個(gè)不確定的變?cè)猣ree_index,那么可以求解出該變?cè)以撟冊(cè)谴_定的.
temp = a[i][var];
for (j = 0; j < var; j++)
{
if (a[i][j] != 0 && j != free_index) temp -= a[i][j] * x[j];
}
x[free_index] = temp / a[i][free_index]; // 求出該變?cè)?
free_x[free_index] = 0; // 該變?cè)谴_定的.
}
return var - k; // 自由變?cè)衯ar - k個(gè).
}
// 3. 唯一解的情況: 在var * (var + 1)的增廣陣中形成嚴(yán)格的上三角陣.
// 計(jì)算出Xn-1, Xn-2 ... X0.
for (i = var - 1; i >= 0; i--)
{
temp = a[i][var];
for (j = i + 1; j < var; j++)
{
if (a[i][j] != 0) temp -= a[i][j] * x[j];
}
if (temp % a[i][i] != 0) return -2; // 說(shuō)明有浮點(diǎn)數(shù)解,但無(wú)整數(shù)解.
x[i] = temp / a[i][i];
}
return 0;
}
int main(void)
{
freopen("Input.txt", "r", stdin);
int i, j;
while (scanf("%d %d", &equ, &var) != EOF)
{
memset(a, 0, sizeof(a));
memset(x, 0, sizeof(x));
memset(free_x, 1, sizeof(free_x)); // 一開(kāi)始全是不確定的變?cè)?
for (i = 0; i < equ; i++)
{
for (j = 0; j < var + 1; j++)
{
scanf("%d", &a[i][j]);
}
}
// Debug();
free_num = Gauss();
if (free_num == -1) printf("無(wú)解!\n");
else if (free_num == -2) printf("有浮點(diǎn)數(shù)解,無(wú)整數(shù)解!\n");
else if (free_num > 0)
{
printf("無(wú)窮多解! 自由變?cè)獋€(gè)數(shù)為%d\n", free_num);
for (i = 0; i < var; i++)
{
if (free_x[i]) printf("x%d 是不確定的\n", i + 1);
else printf("x%d: %d\n", i + 1, x[i]);
}
}
else
{
for (i = 0; i < var; i++)
{
printf("x%d: %d\n", i + 1, x[i]);
}
}
printf("\n");
}
return 0;
}
轉(zhuǎn)自:http://hi.baidu.com/czyuan_acm/blog/item/ebf41f8fdc0e1ee6f01f36e9.html

Sometimes the most important history, is the history we are making today~
聽(tīng)說(shuō)電視連續(xù)劇《蝸居》被禁了,據(jù)說(shuō)是因?yàn)榕_(tái)詞有點(diǎn)黃。果真如此嗎?帶著好奇,我從網(wǎng)上在線看了《蝸居》。一集一集地、認(rèn)認(rèn)真真地看了一遍。邊看邊同情、邊看邊感嘆,邊看邊思考。不把心里的話說(shuō)出來(lái),我悶得慌。
我看《蝸居》的被禁,跟臺(tái)詞黃不黃沒(méi)關(guān)系,大多是個(gè)禁它的借口。再熱播下去,怕要出大亂子。一個(gè)月來(lái),這部電視劇引起了很多人的關(guān)注和網(wǎng)上的熱烈討論。它將鏡頭對(duì)準(zhǔn)了大城市中不那么光鮮的一面:房?jī)r(jià)的上漲以及由此給年輕人的理想造成的巨大沖擊。我們自己的生活就像劇中描寫的一樣,一切都暴露在了陽(yáng)光下。劇中把房子帶來(lái)的社會(huì)問(wèn)題推上極致,這種殘酷的生活直抵每一個(gè)因房?jī)r(jià)而困擾生活的人。
一項(xiàng)36萬(wàn)多人參加的投票調(diào)查中,大多數(shù)人認(rèn)為“幸福與房子關(guān)聯(lián)密切。” “還房貸、吃盒飯”,已經(jīng)成為房?jī)r(jià)飆升年代對(duì)白領(lǐng)生存狀況的一種直白描摹。主人公一波三折的買房奮斗史,道出了都市無(wú)房族的困惑:房?jī)r(jià)是“一匹脫韁的野馬”,攢錢的速度永遠(yuǎn)趕不上房?jī)r(jià)上漲的速度。
有人甘心做房奴嗎,不買房子不行嗎?答案是,不行!誰(shuí)會(huì)租房租一輩子?你要說(shuō),沒(méi)錢你就去郊區(qū)甚至農(nóng)村買房子呀。對(duì),可以在郊區(qū)或農(nóng)村買到便宜房子,可是你的工作單位在市區(qū),你怎么辦?是啊,人民有廣泛的自由,有選擇的權(quán)利。可是,你要上學(xué),就得接受高學(xué)費(fèi),你要看病就得接受高收費(fèi),你要住房就要選擇高房?jī)r(jià),除非你不讓孩子上學(xué)、不去看病,不住房子。你有不選擇的自由嗎?沒(méi)有。買房是社會(huì)逼的,是形勢(shì)逼的,是必需的,你可以選擇這,選擇那,你能選擇不住房子嗎!
那,是誰(shuí)逼著群眾做了房奴?是壟斷階層,是官商勾結(jié),是政治腐敗!國(guó)家是人民的,資源是國(guó)家的,理應(yīng)由人民共享。可是利益集團(tuán)利用人民的資源,憑借其壟斷地位要挾人民。看看現(xiàn)實(shí),看看中石油、中石化, 領(lǐng)著巨額財(cái)政補(bǔ)貼,買樓是10億10億的買,不漲價(jià)就斷你車子的油、不漲價(jià)就斷你家的氣,人為制造緊張。中國(guó)移動(dòng),傳播黃色淫穢網(wǎng)絡(luò)的先鋒,哪里還有一丁點(diǎn)的社會(huì)責(zé)任;有線電視,大家都看見(jiàn)了,獨(dú)此一家,不用也得用,不允許你安裝衛(wèi)星電視,查處你!諸如此類,實(shí)在太多。還有無(wú)恥的專家為他們搖旗吶喊:不能因?yàn)楦F人喝不起水就不漲水價(jià),中國(guó)的電價(jià)嚴(yán)重偏低。漲價(jià)是為了節(jié)約資源,更好地服務(wù)于人民,能力外的資本為零,哈哈,令人笑掉大牙……見(jiàn)過(guò)無(wú)恥的,沒(méi)見(jiàn)過(guò)這么無(wú)恥的。
看看劇情吧,權(quán)力支配一切,資本動(dòng)搖人性,利益逼良為娼。權(quán)貴階層可以隨便劫人祖居、淫人妻女、左右一切。同樣是過(guò)年,富人在富麗堂皇充滿溫馨的大房子里,窮人沒(méi)水沒(méi)電點(diǎn)著蠟燭苦熬;群眾頂著加班的壓力努力地工作,不過(guò)取得些微薄的收入,而權(quán)貴的二奶買件衣服隨便一出手就成千上萬(wàn)!這是我們要的和諧社會(huì)嗎?
看到第19集,我,一個(gè)男人,哭了。小貝的幾聲大吼,你以為只是因?yàn)閵Z妻之恨嗎?非也,他喊出了人壓抑已久的東西!
感謝《蝸居》的七個(gè)理由?
上海電視臺(tái)制作的35集電視連續(xù)劇《蝸居》在國(guó)家廣電總局的否認(rèn)禁播中還是被“禁播”了。只有上海東方衛(wèi)視似乎還在播放,不過(guò),大家多數(shù)人已經(jīng)看過(guò)這部電視劇了,原因是網(wǎng)絡(luò)拉近了精神產(chǎn)品制造者與消費(fèi)者的距離。各地方電視臺(tái)電視臺(tái)形式上的禁播,只是一些人的作秀。我覺(jué)得應(yīng)該感謝《蝸居》。
感謝《蝸居》的第一個(gè)理由,它引起爭(zhēng)議。對(duì)《蝸居》的爭(zhēng)議恐怕還要持續(xù)下去,就讓發(fā)展見(jiàn)證或者證明它的必要與否吧!一部有爭(zhēng)議的電視劇起碼說(shuō)明它是有關(guān)注度的,在被受眾的關(guān)注過(guò)程中,既實(shí)現(xiàn)了電視臺(tái)的播放價(jià)值,又實(shí)現(xiàn)了媒體的報(bào)道價(jià)值,還能教育國(guó)人,凈化心靈。在對(duì)《蝸居》的爭(zhēng)議中,國(guó)人慢慢接受它的存在。
感謝《蝸居》的第二理由,它沒(méi)有亂倫。如今,國(guó)人已經(jīng)出離了羞恥的地步,親情、友情(同事情、戰(zhàn)友情)、愛(ài)情等這些永恒的主題已經(jīng)有了重新闡釋的必要和必須了!而《蝸居》緊緊把握社會(huì)倫理道德的底線,沒(méi)有讓姐夫與小姨子發(fā)生任何關(guān)系,也沒(méi)有通過(guò)更進(jìn)一步的亂倫實(shí)現(xiàn)讓受眾關(guān)注的目的,這讓一些人感動(dòng)。
感謝《蝸居》的第三個(gè)理由,它寫了拆遷。隨著城市化進(jìn)程的加速發(fā)展,隨著國(guó)家拉動(dòng)內(nèi)需政策的深入執(zhí)行,城市要擴(kuò)展生存空間,老舊小區(qū)以及棚戶區(qū)、平房、貧民區(qū)等都要被拆遷建新的。《蝸居》把存在于拆遷中的核心問(wèn)題全部寫出來(lái),讓觀眾自己感受,讓觀眾自己解決。不管是利益拆遷還是流氓阻遷,都在觀眾的心理。
感謝《蝸居》的第四個(gè)理由,它痛恨腐敗。腐敗是發(fā)展的毒瘤,國(guó)人恨之入骨,尤其是哪些家中或者親戚中沒(méi)有當(dāng)官的人,更是恨不得“吃腐敗分子的肉,喝腐敗分子的血”。當(dāng)然,家中或者親戚中如果有當(dāng)官的腐敗了,那就另當(dāng)別論了!他們會(huì)以此自詡,同時(shí),也會(huì)撈取一些提高生活水平的金錢、名譽(yù)、地位,徹底揭示出國(guó)人的雙重人格。
感謝《蝸居》的第五個(gè)理由,它落筆于被社會(huì)遺忘的角落。過(guò)去組成社會(huì)機(jī)構(gòu)的農(nóng)民、工人、知識(shí)分子、商人的階層,現(xiàn)在已經(jīng)發(fā)生了極大的變化:農(nóng)民(農(nóng)民工、農(nóng)電工)、公務(wù)員、工人(礦工)、企業(yè)員工、知識(shí)分子(教師)、領(lǐng)導(dǎo)干部……這些群體都有關(guān)注,也有代言人,也有說(shuō)話的地方,而有一個(gè)群體是沒(méi)有代言人的,是被遺忘的快要發(fā)霉的群體,他們生活在城市夾縫中喘不過(guò)起來(lái),他們以打工名義無(wú)盡地奮斗著,他們是知識(shí)分子,他們有文化,有志向,有力氣,有理想,就是沒(méi)有跳起來(lái)高飛的平臺(tái)。他們每天在一個(gè)企業(yè)里面被老板殘忍的剝奪著,得到的與自己付出的根本不等價(jià),他們的收入被以奉獻(xiàn)的名義剝奪了,加班合理化、扣錢流氓化、養(yǎng)老保險(xiǎn)強(qiáng)制化……就是打個(gè)車還要為城市管理者的無(wú)能埋單。
感謝《蝸居》的第六個(gè)理由,它關(guān)注士階層。記得在中學(xué)的時(shí)候?qū)W習(xí)歷史,講到三國(guó)兩晉南北朝時(shí)期,東晉出現(xiàn)了士階層,他們有錢有勢(shì),生活無(wú)聊,尋找刺激,沒(méi)有追求,攀比成風(fēng),人乳宴就是那個(gè)時(shí)候發(fā)明并且被推廣起來(lái)的。現(xiàn)在這個(gè)新士階層是一個(gè)高度變態(tài)的階層,他們比誰(shuí)的二奶奶多,臉蛋漂亮,歲數(shù)小……并且他們不會(huì)受到內(nèi)心的譴責(zé)的,這是可怕的警示。
感謝《蝸居》的第七個(gè)理由,它打造忍者神龜。好像動(dòng)畫片里有個(gè)東西叫忍者神龜,《蝸居》就是告訴受眾,在這個(gè)社會(huì)生活、生存必須學(xué)會(huì)忍讓,就像烏龜那樣永遠(yuǎn)地蜷縮著自己的腦袋,不要放出了。這樣下去,將讓這個(gè)社會(huì)失去了血性。
來(lái)看看貓撲網(wǎng)收集到的MOPPER的回復(fù)吧
這個(gè)電視劇惡攻精蠅的房地產(chǎn)政策!
沒(méi)看過(guò),但是被禁播一定有它的理由。畢竟話語(yǔ)權(quán)在精英手中。
似乎東方衛(wèi)視還在播。
這是我們要的和諧社會(huì)嗎?
哀民生之多艱!恨權(quán)貴之貪婪!怒官員之腐敗!愧我party之怠慢!
資本主義社會(huì),有多少錢,就有多少自由。你以為法律不禁止,你就自由了?
看到第19集,我,一個(gè)男人,哭了。小貝的幾聲大吼,你以為只是因?yàn)閵Z妻之恨嗎?非也,他喊出了人壓抑已久的東西!
以人為本。以人為本。以人為本。
觸目驚心_____
權(quán)貴的二奶買件衣服隨便一出手就成千上萬(wàn)!這是我們要的和諧社會(huì)嗎?
富人在富麗堂皇充滿溫馨的大房子里,窮人沒(méi)水沒(méi)電點(diǎn)著蠟燭苦熬;群眾頂著加班的壓力努力地工作,不過(guò)取得些微薄的收入
看看劇情吧,權(quán)力支配一切,資本動(dòng)搖人性,利益逼良為娼。權(quán)貴階層可以隨便劫人祖居、淫人妻女、左右一切
無(wú)恥的專家為他們搖旗吶喊:不能因?yàn)楦F人喝不起水就不漲水價(jià),中國(guó)的電價(jià)嚴(yán)重偏低。漲價(jià)是為了節(jié)約資源
不漲價(jià)就斷你車子的油、不漲價(jià)就斷你家的氣,人為制造緊張。中國(guó)移動(dòng),傳播黃色淫穢網(wǎng)絡(luò)的先鋒,哪里還有一丁點(diǎn)的社會(huì)責(zé)任
利益集團(tuán)利用人民的資源,憑借其壟斷地位要挾人民。看看現(xiàn)實(shí),看看中石油、中石化, 領(lǐng)著巨額財(cái)政補(bǔ)貼,買樓是10億10億的買
是誰(shuí)逼著群眾做了房奴?是壟斷階層,是官商勾結(jié),是政治腐敗!國(guó)家是人民的,資源是國(guó)家的,理應(yīng)由人民共享。
見(jiàn)過(guò)無(wú)恥的,沒(méi)見(jiàn)過(guò)這么無(wú)恥的
社會(huì)會(huì)崩潰嗎?房地產(chǎn)很可能就是de-tona-tor.
極有可能,動(dòng)遷的,上訪的,買不起房的,買房被套的,為房當(dāng)二奶的........每個(gè)故事背后都是de-tona-tor,都和房地產(chǎn)有關(guān).........
這樣呵,我也去看看吧。
別當(dāng)真,其實(shí),其色情度,遠(yuǎn)不如……手機(jī)黃段子。關(guān)鍵的“錯(cuò)誤”是……歌頌二奶,大奶很生氣!
盛世危言。
《蝸居》很濫,不過(guò)目前中國(guó)……就是這么濫。濫點(diǎn),一是作者濫情,二是房市濫市,三是官員濫政,四是女性濫性。
——轉(zhuǎn)自天涯
摘要: 這題最簡(jiǎn)單的方法居然是暴力。。。時(shí)間復(fù)雜度一算大概是N^2,AC了。。。
#include<iostream>#include<cstdio>#include<cstring>using namespace std;//暴力求因子,打表 int n;int a[1000001],b[1000001]={0},c...
閱讀全文
摘要: 這個(gè)題我是用線段樹來(lái)做的,結(jié)果居然是超時(shí)。。。后來(lái)foreverlin同學(xué)告訴我他用樹狀數(shù)組過(guò)的,但我記得樹狀數(shù)組能解決的問(wèn)題,線段樹一定能解決,而且線段樹的復(fù)雜度是logL級(jí)別,為什么我會(huì)超時(shí)呢?還請(qǐng)各位大牛指點(diǎn)。。。我的代碼如下:
#include<iostream>#include<cstdio>#include<cstring>#include<...
閱讀全文
久客逢馀閏,他鄉(xiāng)別故人。自然堪下淚,誰(shuí)忍望征塵。
江上風(fēng)煙積,山幽云霧多。送君南浦外,還望將如何。
桂軺雖不駐,蘭筵幸未開(kāi)。林塘風(fēng)月賞,還待故人來(lái)。
霜華凈天末,霧色籠江際。客子常畏人,何為久留滯。
div2的題目確實(shí)比較水,進(jìn)了div1就不同了,除了第一題,后面兩道基本沒(méi)有頭緒。。。。。。不過(guò),樓哥依然還是那么猛。。。。
光榮的回到div2...汗...
Class 1
» GeForce GTX 280M SLI
» Mobility Radeon HD 4870 X2
» GeForce GTX 260M SLI
» GeForce 9800M GTX SLI
» GeForce GTX 280M
» GeForce 9800M GT SLI
» GeForce 9800M GTS SLI
» Mobility Radeon HD 3870 X2
» GeForce 8800M GTX SLI
» Mobility Radeon HD 3850 X2
» Quadro FX 3700M
» Mobility Radeon HD 4870
» Mobility Radeon HD 4860
» FirePro M7740
» Mobility Radeon HD 4850
» GeForce GTX 260M
» GeForce 9800M GTX
» GeForce 9800M GT
» GeForce 8800M GTX
» Quadro FX 3600M
» GeForce GTS 260M
» GeForce GTS 250M
» GeForce GTS 160M
» GeForce 9800M GTS
» GeForce 9800M GS
» Mobility Radeon HD 4830
» GeForce GTS 150M
Class 2
» GeForce 8800M GTS
» Mobility Radeon HD 4670
» GeForce 9700M GTS
» Quadro FX 2700M
» Mobility Radeon HD 3870
» Mobility Radeon HD 4650
» GeForce Go 7950 GTX SLI
» GeForce Go 7900 GTX SLI
» Mobility Radeon HD 3850
» GeForce GT 240M
» GeForce Go 7950 GTX
» Quadro FX 3500M
» GeForce 8700M GT SLI
» GeForce Go 7800 GTX SLI
» GeForce Go 7900 GS SLI
» GeForce Go 7900 GTX
» Quadro FX 2500M
» GeForce 8600M GT SLI
» GeForce GT 230M
» GeForce 9700M GT
» GeForce GT 130M
» GeForce 9650M GT
» GeForce Go 7900 GS
» GeForce 9650M GS
» Quadro FX 1700M
» Quadro FX 1600M
» GeForce 8700M GT
» Quadro NVS 320M
» Quadro FX 1500M
» GeForce 9600M GT
» GeForce GT 220M
» Quadro FX 770M
» GeForce GT 120M
» GeForce Go 7800 GTX
» Mobility Radeon HD 3670
» Mobility FireGL V5725
» Mobility Radeon HD 2600 XT
» Mobility Radeon X1900
» Mobility Radeon X1800XT
» Mobility Radeon X1800
» GeForce Go 6800 Ultra
» GeForce Go 7800
» GeForce 9600M GS
» GeForce 9500M GS
» Mobility Radeon HD 4570
» Mobility Radeon HD 2700
» Mobility Radeon HD 3650
» Mobility FireGL V5700
» Quadro FX 570M
» GeForce 8600M GT
» Mobility Radeon HD 2600
» GeForce Go 7600 GT
Class 3
» GeForce G 210M
» GeForce 9500M G
» GeForce 8600M GS
» GeForce Go 7700
» GeForce Go 6800
» Quadro FX Go 1400
» Mobility Radeon X800XT
» Mobility Radeon HD 4530
» Mobility Radeon X1700
» Mobility FireGL V5250
» Mobility Radeon X2500
» GeForce Go 7600
» Quadro NVS 300M
» Mobility Radeon X800
» Mobility Radeon X1600
» Mobility FireGL V5200
» Mobility Radeon 9800
» GeForce Go 6600
» Mobility Radeon X1450
» Mobility Radeon X700
» Mobility FireGL V5000
» GeForce G 110M
» Mobility Radeon HD 4330
» GeForce 8400M GT
» Quadro NVS 140M
» GeForce G 105M
» GeForce 9500M GE
» GeForce G 102M
» GeForce 9400M (G)
» Mobility Radeon HD 3470 Hybrid X2
» GeForce 9400M GeForceBoost
» Mobility Radeon HD 3470
» GeForce 9300M G
» GeForce 9300M GS
» Quadro FX 370M
» Quadro NVS 160M
» GeForce 9200M GS
» Mobility Radeon HD 3450
» Mobility Radeon HD 3430
» Mobility Radeon HD 3410
» Radeon HD 4200
» Quadro NVS 150M
» Mobility Radeon HD 2400 XT
» Quadro FX 360M
» Mobility Radeon X1350
» Mobility Radeon X1400
» GeForce 9100M G
» GeForce 8400M GS
» Quadro NVS 135M
» Mobility Radeon HD 2400
» Radeon HD 3200
» Radeon HD 3100
» Graphics Media Accelerator (GMA) 4700MHD
» GeForce 8400M G
» Graphics Media Accelerator (GMA) 4500MHD
» Graphics Media Accelerator (GMA) 4500M
» Quadro NVS 130M
» GeForce 8200M G
» GeForce Go 7400
» Quadro FX 350M
» Quadro NVS 120M
» GeForce Go 7300
» Quadro NVS 110M
» Mobility Radeon X600
» Mobility FireGL V3200
» Mobility FireGL V3100
» Mobility Radeon X2300
» Mobility Radeon HD 2300
» Mobility Radeon 9700
» Mobility FireGL T2e
Class 4
» Mobility Radeon X1300
» GeForce4 4200 Go
» Mobility Radeon 9600
» Mobility FireGL T2
» Mobility Radeon 9550
» GeForce Go 7200
» GeForce Go 6400
» Mobility Radeon X300
» GeForce Go 6250
» GeForce Go 6200
» GeForce FX Go 5700
» Quadro FX Go 1000
» GeForce FX Go 5600 / 5650
Class 5
» Radeon Xpress X1270
» Radeon Xpress X1250
» Radeon Xpress 1250
» Radeon Xpress X1200
» Graphics Media Accelerator (GMA) X3100
» Radeon Xpress 1150
» GeForce 7150M
» GeForce Go 6150
» GeForce Go 6100
» GeForce 7000M
» Mobility Radeon 9200
» GeForce FX Go 5200
» Mobility Radeon 9000
» GeForce 4 488 Go
» GeForce 4 460 Go
» GeForce 4 440 Go
» GeForce 4 420 Go
» Graphics Media Accelerator (GMA) 950
» Mobility Radeon 7500
» Mobility FireGL 7800
» Graphics Media Accelerator (GMA) 900
» Radeon Xpress 200M
» Radeon Xpress 1100
Class 6
» Mobility FireGL 9000
» Mirage 3+ 672MX
» Mirage 3 671MX
» Graphics Media Accelerator (GMA) 500
» GeForce 3 Go
» GeForce 2 Go (200 / 100)
» Mobility Radeon 9100 IGP
» Mobility Radeon 9000 IGP
» Mobility Radeon M7
» Mobility Radeon M6
» Mobility Radeon 7000 IGP
» Chrome9 HC
» Extreme Graphics 2
» Radeon IGP 340M
» S3G UniChrome Pro II
» S3G UniChrome Pro
» Mirage 2 M760
» Mirage M661FX
» S3 Graphics ProSavage8
» Castle Rock
» Mobility 128 M3
» SM502
摘要:白盒測(cè)試作為測(cè)試人員常用的一種測(cè)試方法,越來(lái)越受到測(cè)試工程師的重視。白盒測(cè)試并不是簡(jiǎn)單的按照代碼設(shè)計(jì)用例,而是需要根據(jù)不同的測(cè)試需求,結(jié)合不同的測(cè)試對(duì)象,使用適合的方法進(jìn)行測(cè)試。因?yàn)閷?duì)于不同復(fù)雜度的代碼邏輯,可以衍生出許多種執(zhí)行路徑,只有適當(dāng)?shù)臏y(cè)試方法,才能幫助我們從代碼的迷霧森林中找到正確的方向。本文介紹六種白盒子測(cè)試方法:語(yǔ)句覆蓋、判定覆蓋、條件覆蓋、判定條件覆蓋、條件組合覆蓋、路徑覆蓋。
白盒測(cè)試的概述
由于邏輯錯(cuò)誤和不正確假設(shè)與一條程序路徑被運(yùn)行的可能性成反比。由于我們經(jīng)常相信某邏輯路徑不可能被執(zhí)行, 而事實(shí)上,它可能在正常的情況下被執(zhí)行。由于代碼中的筆誤是隨機(jī)且無(wú)法杜絕的,因此我們要進(jìn)行白盒測(cè)試。
白盒測(cè)試又稱結(jié)構(gòu)測(cè)試,透明盒測(cè)試、邏輯驅(qū)動(dòng)測(cè)試或基于代碼的測(cè)試。白盒測(cè)試是一種測(cè)試用例設(shè)計(jì)方法,盒子指的是被測(cè)試的軟件,白盒指的是盒子是可視的,你清楚盒子內(nèi)部的東西以及里面是如何運(yùn)作的。
白盒的測(cè)試用例需要做到:
·保證一個(gè)模塊中的所有獨(dú)立路徑至少 被使用一次
·對(duì)所有邏輯值均需測(cè)試 true 和 false
·在上下邊界及可操作范圍內(nèi)運(yùn)行所有循環(huán)
·檢查內(nèi)部數(shù)據(jù)結(jié)構(gòu)以確保其有效性
白盒測(cè)試的目的:通過(guò)檢查軟件內(nèi)部的邏輯結(jié)構(gòu),對(duì)軟件中的邏輯路徑進(jìn)行覆蓋測(cè)試;在程序不同地方設(shè)立檢查點(diǎn),檢查程序的狀態(tài),以確定實(shí)際運(yùn)行狀態(tài)與預(yù)期狀態(tài)是否一致。
白盒測(cè)試的特點(diǎn):依據(jù)軟件設(shè)計(jì)說(shuō)明書進(jìn)行測(cè)試、對(duì)程序內(nèi)部細(xì)節(jié)的嚴(yán)密檢驗(yàn)、針對(duì)特定條件設(shè)計(jì)測(cè)試用例、對(duì)軟件的邏輯路徑進(jìn)行覆蓋測(cè)試。
白盒測(cè)試的實(shí)施步驟:
1.測(cè)試計(jì)劃階段:根據(jù)需求說(shuō)明書,制定測(cè)試進(jìn)度。
2.測(cè)試設(shè)計(jì)階段:依據(jù)程序設(shè)計(jì)說(shuō)明書,按照一定規(guī)范化的方法進(jìn)行軟件結(jié)構(gòu)劃分和設(shè)計(jì)測(cè)試用例。
3.測(cè)試執(zhí)行階段:輸入測(cè)試用例,得到測(cè)試結(jié)果。
4.測(cè)試總結(jié)階段:對(duì)比測(cè)試的結(jié)果和代碼的預(yù)期結(jié)果,分析錯(cuò)誤原因,找到并解決錯(cuò)誤。
白盒測(cè)試的方法:總體上分為靜態(tài)方法和動(dòng)態(tài)方法兩大類。
靜態(tài)分析是一種不通過(guò)執(zhí)行程序而進(jìn)行測(cè)試的技術(shù)。靜態(tài)分析的關(guān)鍵功能是檢查軟件的表示和描述是否一致,沒(méi)有沖突或者沒(méi)有歧義。
動(dòng)態(tài)分析的主要特點(diǎn)是當(dāng)軟件系統(tǒng)在模擬的或真實(shí)的環(huán)境中執(zhí)行之前、之中和之后 , 對(duì)軟件系統(tǒng)行為的分析。動(dòng)態(tài)分析包含了程序在受控的環(huán)境下使用特定的期望結(jié)果進(jìn)行正式的運(yùn)行。它顯示了一個(gè)系統(tǒng)在檢查狀態(tài)下是正確還是不正確。在動(dòng)態(tài)分析技術(shù)中,最重要的技術(shù)是路徑和分支測(cè)試。下面要介紹的六種覆蓋測(cè)試方法屬于動(dòng)態(tài)分析方法。
白盒測(cè)試的優(yōu)缺點(diǎn)
1. 優(yōu)點(diǎn)
·迫使測(cè)試人員去仔細(xì)思考軟件的實(shí)現(xiàn)
·可以檢測(cè)代碼中的每條分支和路徑
·揭示隱藏在代碼中的錯(cuò)誤
·對(duì)代碼的測(cè)試比較徹底
·最優(yōu)化
2. 缺點(diǎn)
·昂貴
·無(wú)法檢測(cè)代碼中遺漏的路徑和數(shù)據(jù)敏感性錯(cuò)誤
·不驗(yàn)證規(guī)格的正確性
六種覆蓋方法
首先為了下文的舉例描述方便,這里先給出一張程序流程圖。(本文以1995年軟件設(shè)計(jì)師考試的一道考試題目為例,圖中紅色字母代表程序執(zhí)行路徑)。
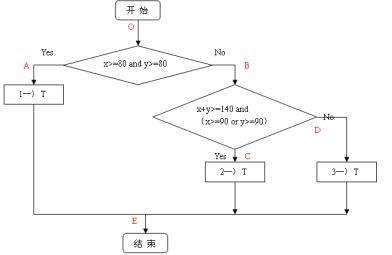
1、語(yǔ)句覆蓋
1)主要特點(diǎn):語(yǔ)句覆蓋是最起碼的結(jié)構(gòu)覆蓋要求,語(yǔ)句覆蓋要求設(shè)計(jì)足夠多的測(cè)試用例,使得程序中每條語(yǔ)句至少被執(zhí)行一次。
2)用例設(shè)計(jì):(如果此時(shí)將A路徑上的語(yǔ)句1—〉T去掉,那么用例如下)
|
|
X
|
Y
|
路徑
|
|
1
|
50
|
50
|
OBDE
|
|
2
|
90
|
70
|
OBCE
|
3)優(yōu)點(diǎn):可以很直觀地從源代碼得到測(cè)試用例,無(wú)須細(xì)分每條判定表達(dá)式。
4)缺點(diǎn):由于這種測(cè)試方法僅僅針對(duì)程序邏輯中顯式存在的語(yǔ)句,但對(duì)于隱藏的條件和可能到達(dá)的隱式邏輯分支,是無(wú)法測(cè)試的。在本例中去掉了語(yǔ)句1—〉T去掉,那么就少了一條測(cè)試路徑。在if結(jié)構(gòu)中若源代碼沒(méi)有給出else后面的執(zhí)行分支,那么語(yǔ)句覆蓋測(cè)試就不會(huì)考慮這種情況。但是我們不能排除這種以外的分支不會(huì)被執(zhí)行,而往往這種錯(cuò)誤會(huì)經(jīng)常出現(xiàn)。再如,在Do-While結(jié)構(gòu)中,語(yǔ)句覆蓋執(zhí)行其中某一個(gè)條件分支。那么顯然,語(yǔ)句覆蓋對(duì)于多分支的邏輯運(yùn)算是無(wú)法全面反映的,它只在乎運(yùn)行一次,而不考慮其他情況。
2、判定覆蓋
1)主要特點(diǎn):判定覆蓋又稱為分支覆蓋,它要求設(shè)計(jì)足夠多的測(cè)試用例,使得程序中每個(gè)判定至少有一次為真值,有一次為假值,即:程序中的每個(gè)分支至少執(zhí)行一次。每個(gè)判斷的取真、取假至少執(zhí)行一次。
2)用例設(shè)計(jì):
|
|
X
|
Y
|
路徑
|
|
1
|
90
|
90
|
OAE
|
|
2
|
50
|
50
|
OBDE
|
|
3
|
90
|
70
|
OBCE
|
3)優(yōu)點(diǎn):判定覆蓋比語(yǔ)句覆蓋要多幾乎一倍的測(cè)試路徑,當(dāng)然也就具有比語(yǔ)句覆蓋更強(qiáng)的測(cè)試能力。同樣判定覆蓋也具有和語(yǔ)句覆蓋一樣的簡(jiǎn)單性,無(wú)須細(xì)分每個(gè)判定就可以得到測(cè)試用例。
4)缺點(diǎn):往往大部分的判定語(yǔ)句是由多個(gè)邏輯條件組合而成(如,判定語(yǔ)句中包含AND、OR、CASE),若僅僅判斷其整個(gè)最終結(jié)果,而忽略每個(gè)條件的取值情況,必然會(huì)遺漏部分測(cè)試路徑。
3、條件覆蓋
1)主要特點(diǎn):條件覆蓋要求設(shè)計(jì)足夠多的測(cè)試用例,使得判定中的每個(gè)條件獲得各種可能的結(jié)果,即每個(gè)條件至少有一次為真值,有一次為假值。
2)用例設(shè)計(jì):
|
|
X
|
Y
|
路徑
|
|
1
|
90
|
70
|
OBC
|
|
2
|
40
|
|
OBD
|
3)優(yōu)點(diǎn):顯然條件覆蓋比判定覆蓋,增加了對(duì)符合判定情況的測(cè)試,增加了測(cè)試路徑。
4)缺點(diǎn):要達(dá)到條件覆蓋,需要足夠多的測(cè)試用例,但條件覆蓋并不能保證判定覆蓋。條件覆蓋只能保證每個(gè)條件至少有一次為真,而不考慮所有的判定結(jié)果。
4、判定/條件覆蓋
1)主要特點(diǎn):設(shè)計(jì)足夠多的測(cè)試用例,使得判定中每個(gè)條件的所有可能結(jié)果至少出現(xiàn)一次,每個(gè)判定本身所有可能結(jié)果也至少出現(xiàn)一次。
2)用例設(shè)計(jì):
|
|
X
|
Y
|
路徑
|
|
1
|
90
|
90
|
OAE
|
|
2
|
50
|
50
|
OBDE
|
|
3
|
90
|
70
|
OBCE
|
|
4
|
70
|
90
|
OBCE
|
3)優(yōu)點(diǎn):判定/條件覆蓋滿足判定覆蓋準(zhǔn)則和條件覆蓋準(zhǔn)則,彌補(bǔ)了二者的不足。
4)缺點(diǎn):判定/條件覆蓋準(zhǔn)則的缺點(diǎn)是未考慮條件的組合情況。
5、組合覆蓋
1)主要特點(diǎn):要求設(shè)計(jì)足夠多的測(cè)試用例,使得每個(gè)判定中條件結(jié)果的所有可能組合至少出現(xiàn)一次。
2)用例設(shè)計(jì):
|
|
X
|
Y
|
路徑
|
|
1
|
90
|
90
|
OAE
|
|
2
|
90
|
70
|
OBCE
|
|
3
|
90
|
30
|
OBDE
|
|
4
|
70
|
90
|
OBCE
|
|
5
|
30
|
90
|
OBDE
|
|
6
|
70
|
70
|
OBDE
|
|
7
|
50
|
50
|
OBDE
|
3)優(yōu)點(diǎn):多重條件覆蓋準(zhǔn)則滿足判定覆蓋、條件覆蓋和判定/條件覆蓋準(zhǔn)則。更改的判定/條件覆蓋要求設(shè)計(jì)足夠多的測(cè)試用例,使得判定中每個(gè)條件的所有可能結(jié)果至少出現(xiàn)一次,每個(gè)判定本身的所有可能結(jié)果也至少出現(xiàn)一次。并且每個(gè)條件都顯示能單獨(dú)影響判定結(jié)果。
4)缺點(diǎn):線性地增加了測(cè)試用例的數(shù)量。
6、路徑覆蓋
1)主要特點(diǎn):設(shè)計(jì)足夠的測(cè)試用例,覆蓋程序中所有可能的路徑。
2)用例設(shè)計(jì):
|
|
X
|
Y
|
路徑
|
|
1
|
90
|
90
|
OAE
|
|
2
|
50
|
50
|
OBDE
|
|
3
|
90
|
70
|
OBCE
|
|
4
|
70
|
90
|
OBCE
|
3)優(yōu)點(diǎn):這種測(cè)試方法可以對(duì)程序進(jìn)行徹底的測(cè)試,比前面五種的覆蓋面都廣。
4)缺點(diǎn):由于路徑覆蓋需要對(duì)所有可能的路徑進(jìn)行測(cè)試(包括循環(huán)、條件組合、分支選擇等),那么需要設(shè)計(jì)大量、復(fù)雜的測(cè)試用例,使得工作量呈指數(shù)級(jí)增長(zhǎng)。而在有些情況下,一些執(zhí)行路徑是不可能被執(zhí)行的,如:
If (!A)B++;
If (!A)D--;
這兩個(gè)語(yǔ)句實(shí)際只包括了2條執(zhí)行路徑,即A為真或假時(shí)候?qū)和D的處理,真或假不可能都存在,而路徑覆蓋測(cè)試則認(rèn)為是包含了真與假的4條執(zhí)行路徑。這樣不僅降低了測(cè)試效率,而且大量的測(cè)試結(jié)果的累積,也為排錯(cuò)帶來(lái)麻煩。
總結(jié)
白盒測(cè)試是一種被廣泛使用的邏輯測(cè)試方法,是由程序內(nèi)部邏輯驅(qū)動(dòng)的一種單元測(cè)試方法。只有對(duì)程序內(nèi)部十分了解才能進(jìn)行適度有效的白盒測(cè)試。但是貫穿在程序內(nèi)部的邏輯存在著不確定性和無(wú)窮性,尤其對(duì)于大規(guī)模復(fù)雜軟件。因此我們不能窮舉所有的邏輯路徑,即使窮舉也未必會(huì)帶來(lái)好運(yùn)(窮舉不能查出程序邏輯規(guī)則錯(cuò)誤,不能查出數(shù)據(jù)相關(guān)錯(cuò)誤,不能查出程序遺漏的路徑)。
那么正確使用白盒測(cè)試,就要先從代碼分析入手,根據(jù)不同的代碼邏輯規(guī)則、語(yǔ)句執(zhí)行情況,選用適合的覆蓋方法。任何一個(gè)高效的測(cè)試用例,都是針對(duì)具體測(cè)試場(chǎng)景的。邏輯測(cè)試不是片面的測(cè)試正確的結(jié)果或是測(cè)試錯(cuò)誤的結(jié)果,而是盡可能全面地覆蓋每一個(gè)邏輯路徑。