位運算簡介及實用技巧
去年年底寫的關于位運算的日志是這個Blog里少數大受歡迎的文章之一,很多人都希望我能不斷完善那篇文章。后來我看到了不少其它的資料,學習到了更多關于位運算的知識,有了重新整理位運算技巧的想法。從今天起我就開始寫這一系列位運算講解文章,與其說是原來那篇文章的follow-up,不如說是一個remake。當然首先我還是從最基礎的東西說起。
什么是位運算?
程序中的所有數在計算機內存中都是以二進制的形式儲存的。位運算說穿了,就是直接對整數在內存中的二進制位進行操作。比如,and運算本來是一個邏輯運算符,但整數與整數之間也可以進行and運算。舉個例子,6的二進制是110,11的二進制是1011,那么6 and 11的結果就是2,它是二進制對應位進行邏輯運算的結果(0表示False,1表示True,空位都當0處理):
110
AND 1011
----------
0010 --> 2
由于位運算直接對內存數據進行操作,不需要轉成十進制,因此處理速度非常快。當然有人會說,這個快了有什么用,計算6 and 11沒有什么實際意義啊。這一系列的文章就將告訴你,位運算到底可以干什么,有些什么經典應用,以及如何用位運算優化你的程序。
Pascal和C中的位運算符號
下面的a和b都是整數類型,則:
C語言 | Pascal語言
-------+-------------
a & b | a and b
a | b | a or b
a ^ b | a xor b
~a | not a
a << b | a shl b
a >> b | a shr b
注意C中的邏輯運算和位運算符號是不同的。520|1314=1834,但520||1314=1,因為邏輯運算時520和1314都相當于True。同樣的,!a和~a也是有區別的。
各種位運算的使用
=== 1. and運算 ===
and運算通常用于二進制取位操作,例如一個數 and 1的結果就是取二進制的最末位。這可以用來判斷一個整數的奇偶,二進制的最末位為0表示該數為偶數,最末位為1表示該數為奇數.
=== 2. or運算 ===
or運算通常用于二進制特定位上的無條件賦值,例如一個數or 1的結果就是把二進制最末位強行變成1。如果需要把二進制最末位變成0,對這個數or 1之后再減一就可以了,其實際意義就是把這個數強行變成最接近的偶數。
=== 3. xor運算 ===
xor運算通常用于對二進制的特定一位進行取反操作,因為異或可以這樣定義:0和1異或0都不變,異或1則取反。
xor運算的逆運算是它本身,也就是說兩次異或同一個數最后結果不變,即(a xor b) xor b = a。xor運算可以用于簡單的加密,比如我想對我MM說1314520,但怕別人知道,于是雙方約定拿我的生日19880516作為密鑰。1314520 xor 19880516 = 20665500,我就把20665500告訴MM。MM再次計算20665500 xor 19880516的值,得到1314520,于是她就明白了我的企圖。
下面我們看另外一個東西。定義兩個符號#和@(我怎么找不到那個圈里有個叉的字符),這兩個符號互為逆運算,也就是說(x # y) @ y = x。現在依次執行下面三條命令,結果是什么?x <- x # y
y <- x @ y
x <- x @ y
執行了第一句后x變成了x # y。那么第二句實質就是y <- x # y @ y,由于#和@互為逆運算,那么此時的y變成了原來的x。第三句中x實際上被賦值為(x # y) @ x,如果#運算具有交換律,那么賦值后x就變成最初的y了。這三句話的結果是,x和y的位置互換了。
加法和減法互為逆運算,并且加法滿足交換律。把#換成+,把@換成-,我們可以寫出一個不需要臨時變量的swap過程(Pascal)。procedure swap(var a,b:longint);
begin
a:=a + b;
b:=a - b;
a:=a - b;
end;
好了,剛才不是說xor的逆運算是它本身嗎?于是我們就有了一個看起來非常詭異的swap過程:procedure swap(var a,b:longint);
begin
a:=a xor b;
b:=a xor b;
a:=a xor b;
end;
=== 4. not運算 ===
not運算的定義是把內存中的0和1全部取反。使用not運算時要格外小心,你需要注意整數類型有沒有符號。如果not的對象是無符號整數(不能表示負數),那么得到的值就是它與該類型上界的差,因為無符號類型的數是用$0000到$FFFF依次表示的。下面的兩個程序(僅語言不同)均返回65435。var
a:word;
begin
a:=100;
a:=not a;
writeln(a);
end.#include <stdio.h>
int main()
{
unsigned short a=100;
a = ~a;
printf( "%d\n", a );
return 0;
}
如果not的對象是有符號的整數,情況就不一樣了,稍后我們會在“整數類型的儲存”小節中提到。
=== 5. shl運算 ===
a shl b就表示把a轉為二進制后左移b位(在后面添b個0)。例如100的二進制為1100100,而110010000轉成十進制是400,那么100 shl 2 = 400。可以看出,a shl b的值實際上就是a乘以2的b次方,因為在二進制數后添一個0就相當于該數乘以2。
通常認為a shl 1比a * 2更快,因為前者是更底層一些的操作。因此程序中乘以2的操作請盡量用左移一位來代替。
定義一些常量可能會用到shl運算。你可以方便地用1 shl 16 - 1來表示65535。很多算法和數據結構要求數據規模必須是2的冪,此時可以用shl來定義Max_N等常量。
=== 6. shr運算 ===
和shl相似,a shr b表示二進制右移b位(去掉末b位),相當于a除以2的b次方(取整)。我們也經常用shr 1來代替div 2,比如二分查找、堆的插入操作等等。想辦法用shr代替除法運算可以使程序效率大大提高。最大公約數的二進制算法用除以2操作來代替慢得出奇的mod運算,效率可以提高60%。
位運算的簡單應用
有時我們的程序需要一個規模不大的Hash表來記錄狀態。比如,做數獨時我們需要27個Hash表來統計每一行、每一列和每一個小九宮格里已經有哪些數了。此時,我們可以用27個小于2^9的整數進行記錄。例如,一個只填了2和5的小九宮格就用數字18表示(二進制為000010010),而某一行的狀態為511則表示這一行已經填滿。需要改變狀態時我們不需要把這個數轉成二進制修改后再轉回去,而是直接進行位操作。在搜索時,把狀態表示成整數可以更好地進行判重等操作。這道題是在搜索中使用位運算加速的經典例子。以后我們會看到更多的例子。
下面列舉了一些常見的二進制位的變換操作。
功能 | 示例 | 位運算
----------------------+---------------------------+--------------------
去掉最后一位 | (101101->10110) | x shr 1
在最后加一個0 | (101101->1011010) | x shl 1
在最后加一個1 | (101101->1011011) | x shl 1+1
把最后一位變成1 | (101100->101101) | x or 1
把最后一位變成0 | (101101->101100) | x or 1-1
最后一位取反 | (101101->101100) | x xor 1
把右數第k位變成1 | (101001->101101,k=3) | x or (1 shl (k-1))
把右數第k位變成0 | (101101->101001,k=3) | x and not (1 shl (k-1))
右數第k位取反 | (101001->101101,k=3) | x xor (1 shl (k-1))
取末三位 | (1101101->101) | x and 7
取末k位 | (1101101->1101,k=5) | x and (1 shl k-1)
取右數第k位 | (1101101->1,k=4) | x shr (k-1) and 1
把末k位變成1 | (101001->101111,k=4) | x or (1 shl k-1)
末k位取反 | (101001->100110,k=4) | x xor (1 shl k-1)
把右邊連續的1變成0 | (100101111->100100000) | x and (x+1)
把右起第一個0變成1 | (100101111->100111111) | x or (x+1)
把右邊連續的0變成1 | (11011000->11011111) | x or (x-1)
取右邊連續的1 | (100101111->1111) | (x xor (x+1)) shr 1
去掉右起第一個1的左邊 | (100101000->1000) | x and (x xor (x-1))
最后這一個在樹狀數組中會用到。
Pascal和C中的16進制表示
Pascal中需要在16進制數前加$符號表示,C中需要在前面加0x來表示。這個以后我們會經常用到。
整數類型的儲存
我們前面所說的位運算都沒有涉及負數,都假設這些運算是在unsigned/word類型(只能表示正數的整型)上進行操作。但計算機如何處理有正負符號的整數類型呢?下面兩個程序都是考察16位整數的儲存方式(只是語言不同)。var
a,b:integer;
begin
a:=$0000;
b:=$0001;
write(a,' ',b,' ');
a:=$FFFE;
b:=$FFFF;
write(a,' ',b,' ');
a:=$7FFF;
b:=$8000;
writeln(a,' ',b);
end.#include <stdio.h>
int main()
{
short int a, b;
a = 0x0000;
b = 0x0001;
printf( "%d %d ", a, b );
a = 0xFFFE;
b = 0xFFFF;
printf( "%d %d ", a, b );
a = 0x7FFF;
b = 0x8000;
printf( "%d %d\n", a, b );
return 0;
}
兩個程序的輸出均為0 1 -2 -1 32767 -32768。其中前兩個數是內存值最小的時候,中間兩個數則是內存值最大的時候,最后輸出的兩個數是正數與負數的分界處。由此你可以清楚地看到計算機是如何儲存一個整數的:計算機用$0000到$7FFF依次表示0到32767的數,剩下的$8000到$FFFF依次表示-32768到-1的數。32位有符號整數的儲存方式也是類似的。稍加注意你會發現,二進制的第一位是用來表示正負號的,0表示正,1表示負。這里有一個問題:0本來既不是正數,也不是負數,但它占用了$0000的位置,因此有符號的整數類型范圍中正數個數比負數少一個。對一個有符號的數進行not運算后,最高位的變化將導致正負顛倒,并且數的絕對值會差1。也就是說,not a實際上等于-a-1。這種整數儲存方式叫做“補碼”。
===== 真正強的東西來了! =====
二進制中的1有奇數個還是偶數個
我們可以用下面的代碼來計算一個32位整數的二進制中1的個數的奇偶性,當輸入數據的二進制表示里有偶數個數字1時程序輸出0,有奇數個則輸出1。例如,1314520的二進制101000000111011011000中有9個1,則x=1314520時程序輸出1。var
i,x,c:longint;
begin
readln(x);
c:=0;
for i:=1 to 32 do
begin
c:=c + x and 1;
x:=x shr 1;
end;
writeln( c and 1 );
end.
但這樣的效率并不高,位運算的神奇之處還沒有體現出來。
同樣是判斷二進制中1的個數的奇偶性,下面這段代碼就強了。你能看出這個代碼的原理嗎?var
x:longint;
begin
readln(x);
x:=x xor (x shr 1);
x:=x xor (x shr 2);
x:=x xor (x shr 4);
x:=x xor (x shr 8);
x:=x xor (x shr 16);
writeln(x and 1);
end.
為了說明上面這段代碼的原理,我們還是拿1314520出來說事。1314520的二進制為101000000111011011000,第一次異或操作的結果如下:
00000000000101000000111011011000
XOR 0000000000010100000011101101100
---------------------------------------
00000000000111100000100110110100
得到的結果是一個新的二進制數,其中右起第i位上的數表示原數中第i和i+1位上有奇數個1還是偶數個1。比如,最右邊那個0表示原數末兩位有偶數個1,右起第3位上的1就表示原數的這個位置和前一個位置中有奇數個1。對這個數進行第二次異或的結果如下:
00000000000111100000100110110100
XOR 000000000001111000001001101101
---------------------------------------
00000000000110011000101111011001
結果里的每個1表示原數的該位置及其前面三個位置中共有奇數個1,每個0就表示原數對應的四個位置上共偶數個1。一直做到第五次異或結束后,得到的二進制數的最末位就表示整個32位數里有多少個1,這就是我們最終想要的答案。
計算二進制中的1的個數
同樣假設x是一個32位整數。經過下面五次賦值后,x的值就是原數的二進制表示中數字1的個數。比如,初始時x為1314520(網友抓狂:能不能換一個數啊),那么最后x就變成了9,它表示1314520的二進制中有9個1。x := (x and $55555555) + ((x shr 1) and $55555555);
x := (x and $33333333) + ((x shr 2) and $33333333);
x := (x and $0F0F0F0F) + ((x shr 4) and $0F0F0F0F);
x := (x and $00FF00FF) + ((x shr 8) and $00FF00FF);
x := (x and $0000FFFF) + ((x shr 16) and $0000FFFF);
為了便于解說,我們下面僅說明這個程序是如何對一個8位整數進行處理的。我們拿數字211(我們班某MM的生日)來開刀。211的二進制為11010011。
+---+---+---+---+---+---+---+---+
| 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | <---原數
+---+---+---+---+---+---+---+---+
| 1 0 | 0 1 | 0 0 | 1 0 | <---第一次運算后
+-------+-------+-------+-------+
| 0 0 1 1 | 0 0 1 0 | <---第二次運算后
+---------------+---------------+
| 0 0 0 0 0 1 0 1 | <---第三次運算后,得數為5
+-------------------------------+
整個程序是一個分治的思想。第一次我們把每相鄰的兩位加起來,得到每兩位里1的個數,比如前兩位10就表示原數的前兩位有2個1。第二次我們繼續兩兩相加,10+01=11,00+10=10,得到的結果是00110010,它表示原數前4位有3個1,末4位有2個1。最后一次我們把0011和0010加起來,得到的就是整個二進制中1的個數。程序中巧妙地使用取位和右移,比如第二行中$33333333的二進制為00110011001100....,用它和x做and運算就相當于以2為單位間隔取數。shr的作用就是讓加法運算的相同數位對齊。
二分查找32位整數的前導0個數
這里用的C語言,我直接Copy的Hacker's Delight上的代碼。這段代碼寫成C要好看些,寫成Pascal的話會出現很多begin和end,搞得代碼很難看。程序思想是二分查找,應該很簡單,我就不細說了。int nlz(unsigned x)
{
int n;
if (x == 0) return(32);
n = 1;
if ((x >> 16) == 0) {n = n +16; x = x <<16;}
if ((x >> 24) == 0) {n = n + 8; x = x << 8;}
if ((x >> 28) == 0) {n = n + 4; x = x << 4;}
if ((x >> 30) == 0) {n = n + 2; x = x << 2;}
n = n - (x >> 31);
return n;
}
只用位運算來取絕對值
這是一個非常有趣的問題。大家先自己想想吧,Ctrl+A顯示答案。
答案:假設x為32位整數,則x xor (not (x shr 31) + 1) + x shr 31的結果是x的絕對值
x shr 31是二進制的最高位,它用來表示x的符號。如果它為0(x為正),則not (x shr 31) + 1等于$00000000,異或任何數結果都不變;如果最高位為1(x為負),則not (x shr 31) + 1等于$FFFFFFFF,x異或它相當于所有數位取反,異或完后再加一。
高低位交換
這個題實際上是我出的,做為學校內部NOIp模擬賽的第一題。題目是這樣:
給出一個小于2^32的正整數。這個數可以用一個32位的二進制數表示(不足32位用0補足)。我們稱這個二進制數的前16位為“高位”,后16位為“低位”。將它的高低位交換,我們可以得到一個新的數。試問這個新的數是多少(用十進制表示)。
例如,數1314520用二進制表示為0000 0000 0001 0100 0000 1110 1101 1000(添加了11個前導0補足為32位),其中前16位為高位,即0000 0000 0001 0100;后16位為低位,即0000 1110 1101 1000。將它的高低位進行交換,我們得到了一個新的二進制數0000 1110 1101 1000 0000 0000 0001 0100。它即是十進制的249036820。
當時幾乎沒有人想到用一句位操作來代替冗長的程序。使用位運算的話兩句話就完了。var
n:dword;
begin
readln( n );
writeln( (n shr 16) or (n shl 16) );
end.
而事實上,Pascal有一個系統函數swap直接就可以用。
二進制逆序
下面的程序讀入一個32位整數并輸出它的二進制倒序后所表示的數。
輸入: 1314520 (二進制為00000000000101000000111011011000)
輸出: 460335104 (二進制為00011011011100000010100000000000)var
x:dword;
begin
readln(x);
x := (x and $55555555) shl 1 or (x and $AAAAAAAA) shr 1;
x := (x and $33333333) shl 2 or (x and $CCCCCCCC) shr 2;
x := (x and $0F0F0F0F) shl 4 or (x and $F0F0F0F0) shr 4;
x := (x and $00FF00FF) shl 8 or (x and $FF00FF00) shr 8;
x := (x and $0000FFFF) shl 16 or (x and $FFFF0000) shr 16;
writeln(x);
end.
它的原理和剛才求二進制中1的個數那個例題是大致相同的。程序首先交換每相鄰兩位上的數,以后把互相交換過的數看成一個整體,繼續進行以2位為單位、以4位為單位的左右對換操作。我們再次用8位整數211來演示程序執行過程:
+---+---+---+---+---+---+---+---+
| 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | <---原數
+---+---+---+---+---+---+---+---+
| 1 1 | 1 0 | 0 0 | 1 1 | <---第一次運算后
+-------+-------+-------+-------+
| 1 0 1 1 | 1 1 0 0 | <---第二次運算后
+---------------+---------------+
| 1 1 0 0 1 0 1 1 | <---第三次運算后
+-------------------------------+
今天我們來看兩個稍微復雜一點的例子。
n皇后問題位運算版
n皇后問題是啥我就不說了吧,學編程的肯定都見過。下面的十多行代碼是n皇后問題的一個高效位運算程序,看到過的人都夸它牛。初始時,upperlim:=(1 shl n)-1。主程序調用test(0,0,0)后sum的值就是n皇后總的解數。拿這個去交USACO,0.3s,暴爽。procedure test(row,ld,rd:longint);
var
pos,p:longint;
begin
{ 1} if row<>upperlim then
{ 2} begin
{ 3} pos:=upperlim and not (row or ld or rd);
{ 4} while pos<>0 do
{ 5} begin
{ 6} p:=pos and -pos;
{ 7} pos:=pos-p;
{ 8} test(row+p,(ld+p)shl 1,(rd+p)shr 1);
{ 9} end;
{10} end
{11} else inc(sum);
end;
乍一看似乎完全摸不著頭腦,實際上整個程序是非常容易理解的。這里還是建議大家自己單步運行一探究竟,實在沒研究出來再看下面的解說。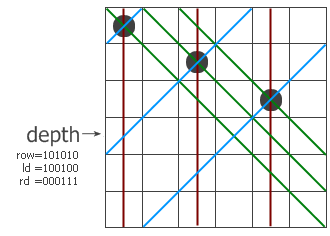
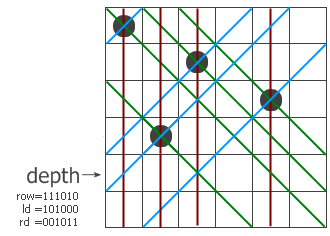
和普通算法一樣,這是一個遞歸過程,程序一行一行地尋找可以放皇后的地方。過程帶三個參數,row、ld和rd,分別表示在縱列和兩個對角線方向的限制條件下這一行的哪些地方不能放。我們以6x6的棋盤為例,看看程序是怎么工作的。假設現在已經遞歸到第四層,前三層放的子已經標在左圖上了。紅色、藍色和綠色的線分別表示三個方向上有沖突的位置,位于該行上的沖突位置就用row、ld和rd中的1來表示。把它們三個并起來,得到該行所有的禁位,取反后就得到所有可以放的位置(用pos來表示)。前面說過-a相當于not a + 1,這里的代碼第6行就相當于pos and (not pos + 1),其結果是取出最右邊的那個1。這樣,p就表示該行的某個可以放子的位置,把它從pos中移除并遞歸調用test過程。注意遞歸調用時三個參數的變化,每個參數都加上了一個禁位,但兩個對角線方向的禁位對下一行的影響需要平移一位。最后,如果遞歸到某個時候發現row=111111了,說明六個皇后全放進去了,此時程序從第1行跳到第11行,找到的解的個數加一。
~~~~====~~~~===== 華麗的分割線 =====~~~~====~~~~
Gray碼
假如我有4個潛在的GF,我需要決定最終到底和誰在一起。一個簡單的辦法就是,依次和每個MM交往一段時間,最后選擇給我帶來的“滿意度”最大的MM。但看了dd牛的理論后,事情開始變得復雜了:我可以選擇和多個MM在一起。這樣,需要考核的狀態變成了2^4=16種(當然包括0000這一狀態,因為我有可能是玻璃)。現在的問題就是,我應該用什么順序來遍歷這16種狀態呢?
傳統的做法是,用二進制數的順序來遍歷所有可能的組合。也就是說,我需要以0000->0001->0010->0011->0100->...->1111這樣的順序對每種狀態進行測試。這個順序很不科學,很多時候狀態的轉移都很耗時。比如從0111到1000時我需要暫時甩掉當前所有的3個MM,然后去把第4個MM。同時改變所有MM與我的關系是一件何等巨大的工程啊。因此,我希望知道,是否有一種方法可以使得,從沒有MM這一狀態出發,每次只改變我和一個MM的關系(追或者甩),15次操作后恰好遍歷完所有可能的組合(最終狀態不一定是1111)。大家自己先試一試看行不行。
解決這個問題的方法很巧妙。我們來說明,假如我們已經知道了n=2時的合法遍歷順序,我們如何得到n=3的遍歷順序。顯然,n=2的遍歷順序如下:
00
01
11
10
你可能已經想到了如何把上面的遍歷順序擴展到n=3的情況。n=3時一共有8種狀態,其中前面4個把n=2的遍歷順序照搬下來,然后把它們對稱翻折下去并在最前面加上1作為后面4個狀態:
000
001
011
010 ↑
--------
110 ↓
111
101
100
用這種方法得到的遍歷順序顯然符合要求。首先,上面8個狀態恰好是n=3時的所有8種組合,因為它們是在n=2的全部四種組合的基礎上考慮選不選第3個元素所得到的。然后我們看到,后面一半的狀態應該和前面一半一樣滿足“相鄰狀態間僅一位不同”的限制,而“鏡面”處則是最前面那一位數不同。再次翻折三階遍歷順序,我們就得到了剛才的問題的答案:
0000
0001
0011
0010
0110
0111
0101
0100
1100
1101
1111
1110
1010
1011
1001
1000
這種遍歷順序作為一種編碼方式存在,叫做Gray碼(寫個中文讓蜘蛛來抓:格雷碼)。它的應用范圍很廣。比如,n階的Gray碼相當于在n維立方體上的Hamilton回路,因為沿著立方體上的邊走一步,n維坐標中只會有一個值改變。再比如,Gray碼和Hanoi塔問題等價。Gray碼改變的是第幾個數,Hanoi塔就該移動哪個盤子。比如,3階的Gray碼每次改變的元素所在位置依次為1-2-1-3-1-2-1,這正好是3階Hanoi塔每次移動盤子編號。如果我們可以快速求出Gray碼的第n個數是多少,我們就可以輸出任意步數后Hanoi塔的移動步驟。現在我告訴你,Gray碼的第n個數(從0算起)是n xor (n shr 1),你能想出來這是為什么嗎?先自己想想吧。
下面我們把二進制數和Gray碼都寫在下面,可以看到左邊的數異或自身右移的結果就等于右邊的數。
二進制數 Gray碼
000 000
001 001
010 011
011 010
100 110
101 111
110 101
111 100
從二進制數的角度看,“鏡像”位置上的數即是對原數進行not運算后的結果。比如,第3個數010和倒數第3個數101的每一位都正好相反。假設這兩個數分別為x和y,那么x xor (x shr 1)和y xor (y shr 1)的結果只有一點不同:后者的首位是1,前者的首位是0。而這正好是Gray碼的生成方法。這就說明了,Gray碼的第n個數確實是n xor (n shr 1)。
今年四月份mashuo給我看了這道題,是二維意義上的Gray碼。題目大意是說,把0到2^(n+m)-1的數寫成2^n * 2^m的矩陣,使得位置相鄰兩數的二進制表示只有一位之差。答案其實很簡單,所有數都是由m位的Gray碼和n位Gray碼拼接而成,需要用左移操作和or運算完成。完整的代碼如下:var
x,y,m,n,u:longint;
begin
readln(m,n);
for x:=0 to 1 shl m-1 do begin
u:=(x xor (x shr 1)) shl n; //輸出數的左邊是一個m位的Gray碼
for y:=0 to 1 shl n-1 do
write(u or (y xor (y shr 1)),' '); //并上一個n位Gray碼
writeln;
end;
end.
下面分享的是我自己寫的三個代碼,里面有些題目也是我自己出的。這些代碼都是在我的Pascal時代寫的,恕不提供C語言了。代碼寫得并不好,我只是想告訴大家位運算在實戰中的應用,包括了搜索和狀態壓縮DP方面的題目。其實大家可以在網上找到更多用位運算優化的題目,這里整理出一些自己寫的代碼,只是為了原創系列文章的完整性。這一系列文章到這里就結束了,希望大家能有所收獲。
Matrix67原創,轉貼請注明出處。
Problem : 費解的開關
題目來源
06年NOIp模擬賽(一) by Matrix67 第四題
問題描述
你玩過“拉燈”游戲嗎?25盞燈排成一個5x5的方形。每一個燈都有一個開關,游戲者可以改變它的狀態。每一步,游戲者可以改變某一個燈的狀態。游戲者改變一個燈的狀態會產生連鎖反應:和這個燈上下左右相鄰的燈也要相應地改變其狀態。
我們用數字“1”表示一盞開著的燈,用數字“0”表示關著的燈。下面這種狀態
10111
01101
10111
10000
11011
在改變了最左上角的燈的狀態后將變成:
01111
11101
10111
10000
11011
再改變它正中間的燈后狀態將變成:
01111
11001
11001
10100
11011
給定一些游戲的初始狀態,編寫程序判斷游戲者是否可能在6步以內使所有的燈都變亮。
輸入格式
第一行有一個正整數n,代表數據中共有n個待解決的游戲初始狀態。
以下若干行數據分為n組,每組數據有5行,每行5個字符。每組數據描述了一個游戲的初始狀態。各組數據間用一個空行分隔。
對于30%的數據,n<=5;
對于100%的數據,n<=500。
輸出格式
輸出數據一共有n行,每行有一個小于等于6的整數,它表示對于輸入數據中對應的游戲狀態最少需要幾步才能使所有燈變亮。
對于某一個游戲初始狀態,若6步以內無法使所有燈變亮,請輸出“-1”。
樣例輸入
3
00111
01011
10001
11010
11100
11101
11101
11110
11111
11111
01111
11111
11111
11111
11111
樣例輸出
3
2
-1
程序代碼const
BigPrime=3214567;
MaxStep=6;
type
pointer=^rec;
rec=record
v:longint;
step:integer;
next:pointer;
end;
var
total:longint;
hash:array[0..BigPrime-1]of pointer;
q:array[1..400000]of rec;
function update(a:longint;p:integer):longint;
begin
a:=a xor (1 shl p);
if p mod 5<>0 then a:=a xor (1 shl (p-1));
if (p+1) mod 5<>0 then a:=a xor (1 shl (p+1));
if p<20 then a:=a xor (1 shl (p+5));
if p>4 then a:=a xor (1 shl (p-5));
exit(a);
end;
function find(a:longint;step:integer):boolean;
var
now:pointer;
begin
now:=hash[a mod BigPrime];
while now<>nil do
begin
if now^.v=a then exit(true);
now:=now^.next;
end;
new(now);
now^.v:=a;
now^.step:=step;
now^.next:=hash[a mod BigPrime];
hash[a mod BigPrime]:=now;
total:=total+1;
exit(false);
end;
procedure solve;
var
p:integer;
close:longint=0;
open:longint=1;
begin
find(1 shl 25-1,0);
q[1].v:=1 shl 25-1;
q[1].step:=0;
repeat
inc(close);
for p:=0 to 24 do
if not find(update(q[close].v,p),q[close].step+1) and (q[close].step+1<MaxStep) then
begin
open:=open+1;
q[open].v:=update(q[close].v,p);
q[open].step:=q[close].step+1;
end;
until close>=open;
end;
procedure print(a:longint);
var
now:pointer;
begin
now:=hash[a mod BigPrime];
while now<>nil do
begin
if now^.v=a then
begin
writeln(now^.step);
exit;
end;
now:=now^.next;
end;
writeln(-1);
end;
procedure main;
var
ch:char;
i,j,n:integer;
t:longint;
begin
readln(n);
for i:=1 to n do
begin
t:=0;
for j:=1 to 25 do
begin
read(ch);
t:=t*2+ord(ch)-48;
if j mod 5=0 then readln;
end;
print(t);
if i<n then readln;
end;
end;
begin
solve;
main;
end.
======================= 性感的分割線 =======================
Problem : garden / 和MM逛花園
題目來源
07年Matrix67生日邀請賽第四題
問題描述
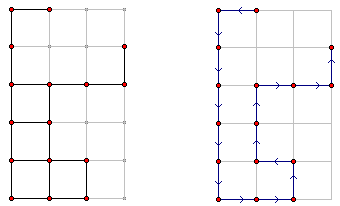
花園設計強調,簡單就是美。Matrix67常去的花園有著非常簡單的布局:花園的所有景點的位置都是“對齊”了的,這些景點可以看作是平面坐標上的格點。相鄰的景點之間有小路相連,這些小路全部平行于坐標軸。景點和小路組成了一個“不完整的網格”。
一個典型的花園布局如左圖所示。花園布局在6行4列的網格上,花園的16個景點的位置用紅色標注在了圖中。黑色線條表示景點間的小路,其余灰色部分實際并不存在。
Matrix67 的生日那天,他要帶著他的MM在花園里游玩。Matrix67不會帶MM兩次經過同一個景點,因此每個景點最多被游覽一次。他和他的MM邊走邊聊,他們是如此的投入以致于他們從不會“主動地拐彎”。也就是說,除非前方已沒有景點或是前方的景點已經訪問過,否則他們會一直往前走下去。當前方景點不存在或已游覽過時,Matrix67會帶MM另選一個方向繼續前進。由于景點個數有限,訪問過的景點將越來越多,遲早會出現不能再走的情況(即四個方向上的相鄰景點都訪問過了),此時他們將結束花園的游覽。Matrix67希望知道以這種方式游覽花園是否有可能遍歷所有的景點。Matrix67可以選擇從任意一個景點開始游覽,以任意一個景點結束。
在上圖所示的花園布局中,一種可能的游覽方式如右圖所示。這種瀏覽方式從(1,2)出發,以(2,4)結束,經過每個景點恰好一次。
輸入格式
第一行輸入兩個用空格隔開的正整數m和n,表示花園被布局在m行n列的網格上。
以下m行每行n個字符,字符“0”表示該位置沒有景點,字符“1”表示對應位置有景點。這些數字之間沒有空格。
輸出格式
你的程序需要尋找滿足“不主動拐彎”性質且遍歷所有景點的游覽路線。
如果沒有這樣的游覽路線,請輸出一行“Impossible”(不帶引號,注意大小寫)。
如果存在游覽路線,請依次輸出你的方案中訪問的景點的坐標,每行輸出一個。坐標的表示格式為“(x,y)”,代表第x行第y列。
如果有多種方案,你只需要輸出其中一種即可。評測系統可以判斷你的方案的正確性。
樣例輸入
6 4
1100
1001
1111
1100
1110
1110
樣例輸出
(1,2)
(1,1)
(2,1)
(3,1)
(4,1)
(5,1)
(6,1)
(6,2)
(6,3)
(5,3)
(5,2)
(4,2)
(3,2)
(3,3)
(3,4)
(2,4)
數據規模
對于30%的數據,n,m<=5;
對于100%的數據,n,m<=10。
程序代碼:program garden;
const
dir:array[1..4,1..2]of integer=
((1,0),(0,1),(-1,0),(0,-1));
type
arr=array[1..10]of integer;
rec=record x,y:integer;end;
var
map:array[0..11,0..11]of boolean;
ans:array[1..100]of rec;
n,m,max:integer;
step:integer=1;
state:arr;
procedure readp;
var
i,j:integer;
ch:char;
begin
readln(m,n);
for i:=1 to n do
begin
for j:=1 to m do
begin
read(ch);
map[i,j]:=(ch='1');
inc(max,ord( map[i,j] ))
end;
readln;
end;
end;
procedure writep;
var
i:integer;
begin
for i:=1 to step do
writeln( '(' , ans[i].x , ',' , ans[i].y , ')' );
end;
procedure solve(x,y:integer);
var
tx,ty,d:integer;
step_cache:integer;
state_cache:arr;
begin
step_cache:=step;
state_cache:=state;
if step=max then
begin
writep;
exit;
end;
for d:=1 to 4 do
begin
tx:=x+dir[d,1];
ty:=y+dir[d,2];
while map[tx,ty] and ( not state[tx] and(1 shl (ty-1) )>0) do
begin
inc(step);
ans[step].x:=tx;
ans[step].y:=ty;
state[tx]:=state[tx] or ( 1 shl (ty-1) );
tx:=tx+dir[d,1];
ty:=ty+dir[d,2];
end;
tx:=tx-dir[d,1];
ty:=ty-dir[d,2];
if (tx<>x) or (ty<>y) then solve(tx,ty);
state:=state_cache;
step:=step_cache;
end;
end;
{====main====}
var
i,j:integer;
begin
assign(input,'garden.in');
reset(input);
assign(output,'garden.out');
rewrite(output);
readp;
for i:=1 to n do
for j:=1 to m do
if map[i,j] then
begin
ans[1].x:=i;
ans[1].y:=j;
state[i]:=1 shl (j-1);
solve(i,j);
state[i]:=0;
end;
close(input);
close(output);
end.
======================= 性感的分割線 =======================
Problem : cowfood / 玉米地
題目來源
USACO月賽
問題描述
農夫約翰購買了一處肥沃的矩形牧場,分成M*N(1<=M<=12; 1<=N<=12)個格子。他想在那里的一些格子中種植美味的玉米。遺憾的是,有些格子區域的土地是貧瘠的,不能耕種。
精明的約翰知道奶牛們進食時不喜歡和別的牛相鄰,所以一旦在一個格子中種植玉米,那么他就不會在相鄰的格子中種植,即沒有兩個被選中的格子擁有公共邊。他還沒有最終確定哪些格子要選擇種植玉米。
作為一個思想開明的人,農夫約翰希望考慮所有可行的選擇格子種植方案。由于太開明,他還考慮一個格子都不選擇的種植方案!請幫助農夫約翰確定種植方案總數。
輸入格式:
第一行:兩個用空格分隔的整數M和N
第二行到第M+1行:第i+1行描述牧場第i行每個格子的情況,N個用空格分隔的整數,表示這個格子是否可以種植(1表示肥沃的、適合種植,0表示貧瘠的、不可種植)
輸出格式
一個整數,農夫約翰可選擇的方案總數除以 100,000,000 的余數
樣例輸入
2 3
1 1 1
0 1 0
樣例輸出
9
樣例說明
給可以種植玉米的格子編號:
1 2 3
4
只種一個格子的方案有四種(1,2,3或4),種植兩個格子的方案有三種(13,14或34),種植三個格子的方案有一種(134),還有一種什么格子都不種。
4+3+1+1=9。
數據規模
對于30%的數據,N,M<=4;
對于100%的數據,N,M<=12。
程序代碼:program cowfood;
const
d=100000000;
MaxN=12;
var
f:array[0..MaxN,1..2000]of longint;
w:array[1..2000,1..2000]of boolean;
st:array[0..2000]of integer;
map:array[0..MaxN]of integer;
m,n:integer;
function Impossible(a:integer):boolean;
var
i:integer;
flag:boolean=false;
begin
for i:=1 to MaxN do
begin
if flag and (a and 1=1) then exit(true);
flag:=(a and 1=1);
a:=a shr 1;
end;
exit(false);
end;
function Conflict(a,b:integer):boolean;
var
i:integer;
begin
for i:=1 to MaxN do
begin
if (a and 1=1) and (b and 1=1) then exit(true);
a:=a shr 1;
b:=b shr 1;
end;
exit(false);
end;
function CanPlace(a,b:integer):boolean;
begin
exit(a or b=b);
end;
procedure FindSt;
var
i:integer;
begin
for i:=0 to 1 shl MaxN-1 do
if not Impossible(i) then
begin
inc(st[0]);
st[st[0]]:=i;
end;
end;
procedure Init;
var
i,j:integer;
begin
for i:=1 to st[0] do
for j:=i to st[0] do
if not Conflict(st[i],st[j]) then
begin
w[i,j]:=true;
w[j,i]:=true;
end;
end;
procedure Readp;
var
i,j,t,v:integer;
begin
readln(m,n);
for i:=1 to m do
begin
v:=0;
for j:=1 to n do
begin
read(t);
v:=v*2+t;
end;
map[i]:=v;
readln;
end;
end;
procedure Solve;
var
i,j,k:integer;
begin
f[0,1]:=1;
map[0]:=1 shl n-1;
for i:=1 to m do
for j:=1 to st[0] do
if not CanPlace(st[j],map[i]) then f[i,j]:=-1 else
for k:=1 to st[0] do if (f[i-1,k]<>-1) and w[j,k] then
f[i,j]:=(f[i,j]+f[i-1,k]) mod d;
end;
procedure Writep;
var
j:integer;
ans:longint=0;
begin
for j:=1 to st[0] do
if f[m,j]<>-1 then ans:=(ans+f[m,j]) mod d;
writeln(ans);
end;
begin
assign(input,'cowfood.in');
reset(input);
assign(output,'cowfood.out');
rewrite(output);
FindSt;
Init;
Readp;
Solve;
Writep;
close(input);
close(output);
end.
轉自:http://www.matrix67.com/blog/archives/268
posted on 2009-09-24 13:22 abilitytao 閱讀(2097) 評論(2) 編輯 收藏 引用