記得去年的校圣誕編程大賽的初賽和復賽中有3，4道類型相似的題目，當時對于剛加入ACMER行列的我并不了解這是哪一類的題目，只覺得這些題目有一定的規律。后來寫的程序多了，接觸的算法也多了，慢慢的知道那3，4道題目其實是動態規劃下的”背包問題”.現在基本上了解了這類題目的解題思路和應對方法,故想借此對各種背包問題做一個詳細的解釋.
0-1背包
0-1背包是基礎,接下來所有背包的問題都會圍繞0-1背包展開,所以我將會特別仔細的進行闡釋.當然0-1背包可以用貪心來完成,考慮到各種背包的通用性,貪心解法我就略過了,直接從動態規劃的解法開始講起.
先從一道例題講起:
0-1原型:
一個旅行者有一個最多能用M公斤的背包，現在有N件物品，
它們的重量分別是W1，W2，...,Wn,
它們的價值分別為P1,P2,...,Pn.
問:每種物品只有一件，則旅行者能獲得的最大總價值是多少?
解答:
其實很多人都能從網上搜到0-1背包的狀態轉移方程,即: f[i][v]=max{f[i-1][v],f[i-1][v-c[i]]+w[i]}.但是對它的靈活運用和具體實現不甚了解，接下來我以這題為例展示此狀態方程的由來，以便接下來后面幾種背包的學習.
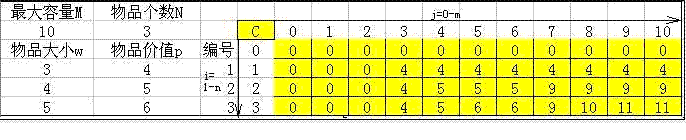
因為背包最大容量M未知。所以，我們的程序要從1到M一個一個的試。比如，開始任選N件物品的一個。看對應M的背包，能不能放進去，如果能放進去，并且還有多的空間，則，多出來的空間里能放N-1物品中的最大價值。怎么能保證總選擇是最大價值呢？
看下表。
測試數據：
10,3
3,4
4,5
5,6
c[i][j]數組保存了1,2,3號物品依次選擇后的最大價值.
這個最大價值是怎么得來的呢?從背包容量為0開始,1號物品先試,0,1,2,的容量都不能放.所以置0,背包容量為3則里面放4.這樣,這一排背包容量為4,5,6,....10的時候，最佳方案都是放4.假如1號物品放入背包.則再看2號物品.當背包容量為3的時候，最佳方案還是上一排的最價方案c為4.而背包容量為5的時候，則最佳方案為自己的重量5.背包容量為7的時候，很顯然是5加上一個值了。加誰??很顯然是7-4=3的時候.上一排 c3的最佳方案是4.所以。總的最佳方案是5+4為9.這樣.一排一排推下去。最右下放的數據就是最大的價值了。(注意第3排的背包容量為7的時候,最佳方案不是本身的6.而是上一排的9.說明這時候3號物品沒有被選.選的是1,2號物品.所以得9.)
從以上最大價值的構造過程中可以看出。
f[i][v]=max{f[i-1][v],f[i-1][v-c[i]]+w[i]} 這就是0-1背包的狀態轉移方程了
/以下是實際程序，此程序來源自網絡
1
/-----------------------------------------------------------------------------------/
2#include<stdio.h>
3
int c[10][100];/**//*對應每種情況的最大價值*/
4int knapsack(int m,int n)
5
{
6
int i,j,w[10],p[10];
7 for(i=1;i<n+1;i++)
8 scanf("\n%d,%d",&w[i],&p[i]);
9 for(i=0;i<10;i++)
10 for(j=0;j<100;j++)
11
c[i][j]=0;/**//*初始化數組*/
12 for(i=1;i<n+1;i++)
13 for(j=1;j<m+1;j++)
14 {
15 if(w[i]<=j) /**//*如果當前物品的容量小于背包容量*/
16 {
17 if(p[i]+c[i-1][j-w[i]]>c[i-1][j])
18 /**//*如果本物品的價值加上背包剩下的空間能放的物品的價值*/
19 /**//*大于上一次選擇的最佳方案則更新c[i][j]*/
20 c[i][j]=p[i]+c[i-1][j-w[i]];
21 else
22 c[i][j]=c[i-1][j];
23
}
24 else c[i][j]=c[i-1][j];
25 }
26 return(c[n][m]);
27
28
}
29int main()
30{
31 int m,n;int i,j;
32 scanf("%d,%d",&m,&n);
33 printf("Input each one:\n");
34 printf("%d",knapsack(m,n));
35 printf("\n");/**//*下面是測試這個數組,可刪除*/
36 for(i=0;i<10;i++)
37 for(j=0;j<15;j++)
38 {
39 printf("%d ",c[i][j]);
40 if(j==14)printf("\n");
41 }
42 system("pause");
43}
44
45/--------------------------------------------------------------------------------------------------------------------/
46/--------------------------------------------------------------------------------------------------------------------/
47
好了繼續，看完上面的解釋，相信你對0-1背包的運作有了基本的了解，下面就來練練手吧.
Bone Collector
Time Limit : 2000/1000ms (Java/Other) Memory Limit : 32768/32768K (Java/Other)
Total Submission(s) : 125 Accepted Submission(s) : 37
Font: Times New Roman | Verdana | Georgia
Font Size: ← →
Problem Description
Many years ago , in Teddy’s hometown there was a man who was called “Bone Collector”. This man like to collect varies of bones , such as dog’s , cow’s , also he went to the grave …
The bone collector had a big bag with a volume of V ,and along his trip of collecting there are a lot of bones , obviously , different bone has different value and different volume, now given the each bone’s value along his trip , can you calculate out the maximum of the total value the bone collector can get ?
Input
The first line contain a integer T , the number of cases.
Followed by T cases , each case three lines , the first line contain two integer N , V, (N <= 1000 , V <= 1000 )representing the number of bones and the volume of his bag. And the second line contain N integers representing the value of each bone. The third line contain N integers representing the volume of each bone.
Output
One integer per line representing the maximum of the total value (this number will be less than 231).
Sample Input
1
5 10
1 2 3 4 5
5 4 3 2 1
Sample Output
14
這是杭電ACM oj 上的題目，是不是和剛才的題目很相似，那就開始動手吧。
寫完可以在http://acm.hdu.edu.cn/diy/contest_showproblem.php?pid=1001&cid=1922上提交試試;
僅供參考的ac程序:
1/**//*
2copyright jj
3hdu-1922
4 2008.12.30
5 狀態:已AC
6*/
7#include<iostream>
8using namespace std;
9int max(int a,int b){
10 int temp;
11 if(a>b) temp=a;
12 else temp=b;
13 return temp;
14}
15int zeroonepack(int n,int m,int v[],int w[],int *maj) //0-1背包部分代碼
16{
17 for(int y=0;y<=m;y++) //初始化行為0
18 maj[y]=0;
19
20 for(int i=1;i<=n;i++) //注意循環的始末
21 for(int j=m;j>=0;j--) //注意此處
22 if(w[i]<=j)
23 maj[j]=max(maj[j],maj[j-w[i]]+v[i]); //最關鍵的狀態轉移方程
24 else
25 maj[j]=maj[j];
26 return maj[m]; //返回最后一行最后一個值
27}
28int main()
29{
30 int times,n,m,*maj;
31 cin>>times;
32 for(int e=0;e<times;e++)
33 {
34 cin>>n>>m;
35 int *w=new int[n+1];
36 for(int r=1;r<=n;r++)
37 cin>>w[r];
38 int *v=new int[n+1];
39 for(int k=1;k<=n;k++)
40 cin>>v[k];
41 maj=new int[m+1];
42
43cout<< zeroonepack(n,m,w,v,maj)<<endl;;
44}
45 return 0;
46}
47
48
49/--------------------------------------------------------------------------------------------------------------------/
50/--------------------------------------------------------------------------------------------------------------------/
51
如果不懂上述代碼,請再回看圖片,接下來我們再來看一道題目
擎天柱
Time Limit:1000MS Memory Limit:32768K
Description:
話說月光家里有許多玩具，最近他又看上了DK新買的“擎天柱”，就想用自己的跟DK的換。每種玩具都有特定的價格，價格為整數。只有月光拿出的玩具的總價格與“擎天柱”的價格相等才能換得“擎天柱”。同時，月光還希望能用最少的玩具數換回“擎天柱”。請問，月光能順利得到夢寐以求的“擎天柱”嗎？
Input:
輸入數據包含多組；對于每組數據，第一行為一個正整數n(1 ≤n≤10); 表示月光手頭有n個玩具。接下來一行有n個正整數P1，P2，……，Pn（1 ≤ Pi ≤ 1000），Pi為第i個玩具的所對應的價格。最后一行為一個正整數m(1 ≤ m ≤10000)，為“擎天柱”的價格。
Output:
對于每組數據，如果能換得“擎天柱”則輸出最少玩具數；否則，輸出“-1”。
Sample Input:
3
1 2 3
4
4
4 3 3 5
2
Sample Output:
2
-1
Source:
這是浙工大ACM上的題目做完可以提交試試
url: http://acm.zjut.edu.cn/ShowProblem.aspx?ShowID=1355
祝你好運！~
想用剛才的方法做？發現題目里多了什么條件沒？
對了！那就是“只有月光拿出的玩具的總價格與“擎天柱”的價格相等才能換得“擎天柱””這句。 換句話說題目要求的不僅僅是最優值而且要求你求的是“能把包裝滿”的最優值！！！
怎么辦？難道就這樣束手無策了么？
解答:
0-1背包也是背包問題的最常見的兩種問法:
一是要求“恰好裝滿背包”時的最優解
二是“沒有要求必須把背包裝滿”。
這兩種問法的實現方法不同點主要在初始化上。
如果是第一種問法，要求恰好裝滿背包，那么在初始化時除了f[0]為0其它f[1..V]均設為-∞，這樣就可以保證最終得到的f[N]是一種恰好裝滿背包的最優解。
如果并沒有要求必須把背包裝滿，而是只希望價格盡量大，初始化時應該將f[0..V]全部設為0。
為什么呢？
可以這樣理解：初始化的f數組事實上就是在沒有任何物品可以放入背包時的合法狀態。如果要求背包恰好裝滿，那么此時只有容量為0的背包可能被價值為0的nothing“恰好裝滿”，其它容量的背包均沒有合法的解，屬于未定義的狀態，它們的值就都應該是-∞了。如果背包并非必須被裝滿，那么任何容量的背包都有一個合法解“什么都不裝”，這個解的價值為0，所以初始時狀態的值也就全部為0了。
這個小技巧完全可以推廣到其它類型的背包問題，后面也就不再對進行狀態轉移之前的初始化進行講解
再來看看我AC的代碼:
1/**//*
2copyright jj
3zjut-1355
4 2009.01.03
5 狀態:已AC
6*/
7#include<iostream>
8#include<stdlib.h>
9using namespace std;
10int n,sum;
11int min(int a,int b){
12 int temp;
13 if(a>b) temp=b;
14 else temp=a;
15 return temp;
16}
17
18int zeroonepack(int a[],int total,int dp[])
19{
20
21 for(int j=1;j<=total;j++) //這是與上題的區別之處，因為這題要求的是最少,所以在初始化時
22dp[j]=1000000; //我選擇了1000000作為無窮大
23 dp[0]=0;
24 for(int p=1;p<=n;p++)
25 for(int q=total;q>=0;q--)
26 if(a[p]<=q)
27 dp[q]=min(dp[q],dp[q-a[p]]+1);
28 else
29 dp[q]=dp[q];
30
31 if(dp[total]!=1000000)
32 return dp[total];
33 else
34 return -1;
35 free(dp);
36
37}
38int main()
39{
40while(cin>>n)
41{
42 int *toy=new int[n+1];
43 for(int i=1;i<=n;i++)
44 cin>>toy[i];
45 cin>>sum;
46 int* dp=new int [sum+1];
47 cout<<zeroonepack(toy,sum,dp)<<endl;
48 free(toy);
49 free(dp);
50}
51 return 0;
52}
53
54
55
56/---------------------------------------------------------------------------------------------------------------------/
57 /---------------------------------------------------------------------------------------------------------------------/
58
59
完全背包
有了對0-1背包的深刻認識，我們終于可以看看它的幾種變形了。首先登場的是完全背包，
何為“完全背包”，就是每樣東西都有無窮多個.
我們還是先來到題目看看究竟吧!~
寒冰王座
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 1889 Accepted Submission(s): 810
Problem Description
不死族的巫妖王發工資拉,死亡騎士拿到一張N元的鈔票(記住,只有一張鈔票),為了防止自己在戰斗中頻繁的死掉,他決定給自己買一些道具,于是他來到了地精商店前.
死亡騎士:"我要買道具!"
地精商人:"我們這里有三種道具,血瓶150塊一個,魔法藥200塊一個,無敵藥水350塊一個."
死亡騎士:"好的,給我一個血瓶."
說完他掏出那張N元的大鈔遞給地精商人.
地精商人:"我忘了提醒你了,我們這里沒有找客人錢的習慣的,多的錢我們都當小費收了的,嘿嘿."
死亡騎士:"......"
死亡騎士想,與其把錢當小費送個他還不如自己多買一點道具,反正以后都要買的,早點買了放在家里也好,但是要盡量少讓他賺小費.
現在死亡騎士希望你能幫他計算一下,最少他要給地精商人多少小費.
Input
輸入數據的第一行是一個整數T(1<=T<=100),代表測試數據的數量.然后是T行測試數據,每個測試數據只包含一個正整數N(1<=N<=10000),N代表死亡騎士手中鈔票的面值.
注意:地精商店只有題中描述的三種道具.
Output
對于每組測試數據,請你輸出死亡騎士最少要浪費多少錢給地精商人作為小費.
Sample Input
2
900
250
Sample Output
0
50
關鍵:
轉化為01背包問題求解
解題思路:
既然01背包問題是最基本的背包問題，那么我們可以考慮把完全背包問題轉化為01背包問題來解。最簡單的想法是，考慮到第i種物品最多選V/c[i]件，于是可以把第i種物品轉化為V/c[i]件費用及價值均不變的物品，然后求解這個01背包問題。這樣完全沒有改進基本思路的時間復雜度，但這畢竟給了我們將完全背包問題轉化為01背包問題的思路：將一種物品拆成多件物品。
但我們有更優的O(VN)的算法。這個算法使用一維數組，先看偽代碼：
for i=1..N
for v=0..V
f[v]=max{f[v],f[v-c[i]]+w[i]};
你會發現，這個偽代碼與0-1背包的偽代碼只有v的循環次序不同而已。為什么這樣一改就可行呢？首先想想為什么0-1背包中要按照v=V..0的逆序來循環。這是因為要保證第i次循環中的狀態f[i][v]是由狀態f[i-1][v-c[i]]遞推而來。換句話說，這正是為了保證每件物品只選一次，保證在考慮“選入第i件物品”這件策略時，依據的是一個絕無已經選入第i件物品的子結果f[i-1][v-c[i]]。而現在完全背包的特點恰是每種物品可選無限件，所以在考慮“加選一件第i種物品”這種策略時，卻正需要一個可能已選入第i種物品的子結果f[i][v-c[i]]，所以就可以并且必須采用v=0..V的順序循環。這就是這個簡單的程序為何成立的道理。
這個算法也可以以另外的思路得出。例如，基本思路中的狀態轉移方程可以等價地變形成這種形式：f[i][v]=max{f[i-1][v],f[i][v-c[i]]+w[i]}，將這個方程用一維數組實現，便得到了上面的偽代碼。
再看看我AC的代碼：
1/**//*
2copyright jj
3hdu-1248
4 2009.01.04
5 狀態:已AC
6*/
7
8#include<iostream>
9using namespace std;
10int n=3,sum;
11int max(int a,int b){
12 int temp;
13 if(a>b) temp=a;
14 else temp=b;
15 return temp;
16}
17
18int completepack(int a[],int total,int dp[])
19{
20
21 for(int j=0;j<=total;j++)
22 dp[j]=0;
23 for(int p=1;p<=n;p++)
24 for(int q=0;q<=total;q++) //解決問題的關鍵點
25 if(a[p]<=q)
26 dp[q]=max(dp[q],dp[q-a[p]]+a[p]);
27 else
28 dp[q]=dp[q];
29
30 return dp[total];
31
32
33}
34int main()
35{
36 int toy[4]={0,150,200,350};
37 int m;
38while(cin>>m)
39{
40 for(int k=0;k<m;k++)
41 {
42 cin>>sum;
43 int* dp=new int [sum+1];
44 cout<<sum-completepack(toy,sum,dp)<<endl;
45 free(dp);
46 }
47
48
49}
50 return 0;
51}
52
53
54
55至于當要求把背包完全裝滿該如何做，我就不再啰嗦了。可以參考0-1背包的解決辦法
56
57
58
59/---------------------------------------------------------------------------------------------------------------------/
60 /---------------------------------------------------------------------------------------------------------------------/
61
62
63
多重背包
當每種物品不是1個也不是無窮多個，而是指定的n個時。就出現了我現在所要說的多重背包問題。
基本算法
這題目和完全背包問題很類似。基本的方程只需將完全背包問題的方程略微一改即可，因為對于第i種物品有n[i]+1種策略：取0件，取1件……取n[i]件。令f[i][v]表示前i種物品恰放入一個容量為v的背包的最大權值，則有狀態轉移方程：
f[i][v]=max{f[i-1][v-k*c[i]]+k*w[i]|0<=k<=n[i]}
復雜度是O(V*Σn[i])。【好慢哦】
轉化為01背包問題
另一種好想好寫的基本方法是轉化為01背包求解：把第i種物品換成n[i]件01背包中的物品，則得到了物品數為Σn[i]的01背包問題，直接求解，復雜度仍然是O(V*Σn[i])。【依然是慢的】
來看一道題目:
Cash Machine
|
Time Limit: 1000MS
|
|
Memory Limit: 10000K
|
|
Total Submissions: 6470
|
|
Accepted: 2075
|
Description
A Bank plans to install a machine for cash withdrawal. The machine is able to deliver appropriate @ bills for a requested cash amount. The machine uses exactly N distinct bill denominations, say Dk, k=1,N, and for each denomination Dk the machine has a supply of nk bills. For example,
N=3, n1=10, D1=100, n2=4, D2=50, n3=5, D3=10
means the machine has a supply of 10 bills of @100 each, 4 bills of @50 each, and 5 bills of @10 each.
Call cash the requested amount of cash the machine should deliver and write a program that computes the maximum amount of cash less than or equal to cash that can be effectively delivered according to the available bill supply of the machine.
Notes:
@ is the symbol of the currency delivered by the machine. For instance, @ may stand for dollar, euro, pound etc.
Input
The program input is from standard input. Each data set in the input stands for a particular transaction and has the format:
cash N n1 D1 n2 D2 ... nN DN
where 0 <= cash <= 100000 is the amount of cash requested, 0 <=N <= 10 is the number of bill denominations and 0 <= nk <= 1000 is the number of available bills for the Dk denomination, 1 <= Dk <= 1000, k=1,N. White spaces can occur freely between the numbers in the input. The input data are correct.
Output
For each set of data the program prints the result to the standard output on a separate line as shown in the examples below.
Sample Input
735 3 4 125 6 5 3 350
633 4 500 30 6 100 1 5 0 1
735 0
0 3 10 100 10 50 10 10
Sample Output
735
630
0
0
是不是老是超時？怎么辦？怎么樣才能把O(V*Σn[i])的時間復雜度給降下來，還有什么地方可以剪枝嗎？
參考思路:
利用二進制的思想，我們考慮把第i種物品換成若干件物品，使得原問題中第i種物品可取的每種策略——取0..n[i]件——均能等價于取若干件代換以后的物品。另外，取超過n[i]件的策略必不能出現。
方法是：將第i種物品分成若干件物品，其中每件物品有一個系數，這件物品的費用和價值均是原來的費用和價值乘以這個系數。使這些系數分別為1,2,4,...,2^(k-1),n[i]-2^k+1，且k是滿足n[i]-2^k+1>0的最大整數。例如，如果n[i]為13，就將這種物品分成系數分別為1,2,4,6的四件物品。
分成的這幾件物品的系數和為n[i]，表明不可能取多于n[i]件的第i種物品。另外這種方法也能保證對于0..n[i]間的每一個整數，均可以用若干個系數的和表示，這個證明可以分0..2^k-1和2^k..n[i]兩段來分別討論得出，并不難，希望你自己思考嘗試一下。
這樣就將第i種物品分成了O(log n[i])種物品，將原問題轉化為了復雜度為
O(V*Σlog n[i])的01背包問題，是很大的改進。
下面給出O(log amount)時間處理一件多重背包中物品的過程，其中amount表示物品的數量：
procedure MultiplePack(cost,weight,amount)
if cost*amount>=V
CompletePack(cost,weight)
return
integer k=1
while k<amount
ZeroOnePack(k*cost,k*weight)
amount=amount-k
k=k*2
ZeroOnePack(amount*cost,amount*weight)
希望你仔細體會這個偽代碼，如果不太理解的話，看看下面我AC的程序，單步執行幾次，或者頭腦加紙筆模擬一下，也許就會慢慢理解了。
再看看我AC的代碼,幫助你進一步的理解這類問題:
1/**//*
2copyright jj
3pku-1276
4 2009.02.11
5 狀態:已AC
6*/
7
8#include<iostream>
9using namespace std;
10
11
12int V;
13int huafei[11],n,geshu[11],*dp;
14
15int max(int a,int b){ return a>b?a:b;}
16void zeroonepack(int cost,int weight) //0-1背包的運用
17{
18 for(int v1=V;v1>=0;v1--)
19 if(cost<=v1)
20 dp[v1]=max(dp[v1],dp[v1-cost]+weight);
21 else
22 dp[v1]=dp[v1];
23}
24
25void completepack(int cost,int weight) //完全背包的運用
26{
27 for(int v2=0;v2<=V;v2++)
28 if(cost<=v2)
29 dp[v2]=max(dp[v2],dp[v2-cost]+weight);
30 else
31 dp[v2]=dp[v2];
32}
33
34
35void multiplepack(int cost ,int weight,int amount) //最后合成多重背包
36{
37 if(amount*cost>V)
38 {
39 completepack(cost,weight);
40 return ;
41 }
42
43 int k=1;
44 while(k<amount)
45 {
46 zeroonepack(k*cost,k*weight);
47 amount-=k;
48 k*=2;
49 }
50 zeroonepack(amount*cost,amount*weight);
51}
52
53int main()
54{
55 while(cin>>V>>n)
56 {
57 dp=new int[V+1];
58 for(int i=1;i<=n;i++)
59 cin>>geshu[i]>>huafei[i];
60 for(int q=0;q<=V;q++)
61 dp[q]=0;
62 for(int j=1;j<=n;j++)
63 multiplepack(huafei[j],huafei[j],geshu[j]);
64
65 cout<<dp[V]<<endl;
66 free(dp);
67 }
68 return 0;
69}
70
這樣O(log amount)的算法就搞定了。嘿嘿~
尾聲
關于背包問題的問法，我還想再多說兩句，但不做詳細的解釋,只供有興趣的人延伸閱讀
比如1：
要求你在輸出最優方案的同時要求你把選擇的方案輸出?這該怎么做？
比如2：
要求你輸出字典序最小的最優方案？又該怎么辦？
比如3：
要求你求出最優方案的總數？那又是怎么樣的？
背包問題的變種還是非常多的,當然都是在0-1背包的基礎上進行修改的。在經歷了去年的圣誕賽后，我也專門研究了一下各種背包問題。在學習過程中主要的參考資料是dd牛的《背包九講》,而以上的題目和代碼均為自己在學習過程中碰到并解決的，所以特別編輯在了一起希望以后學習背包的人能少走彎路。
Jj
2009-5-27
轉自:http://www.shnenglu.com/jinjiankla/archive/2009/07/23/90954.html