題目描述：
Luck is the key to life. When I have to decide something, I will make my decision by flipping a coin. And then, I have two things to do. First, I have the decision made. Second, I go to the nearest church and donate the coin.
But there are always too many things I have to decide. For example, what should I eat today for lunch? OK, now we are talking about a decision, so let us assume that I have two kinds of food: quick-served noodle A and quick-served noodle B.
I just have bought N bowls of noodle A and N bowls of noodle B. If I have some space to make a decision (i.e. having two kinds of quick-served noodle to choose from), then I will flip a coin to decide which kind of noodle to eat.
My question is, before I eat up all 2 * N bowls of quick-served noodle, what is the mathematical expectation of the number of coins I will have to donate.
Input
Standard input will contain multiple test cases. The first line of the input is a single integer T (1 <= T <= 1000) which is the number of test cases. And it will be followed by T consecutive test cases.
Each test case contains an integer N (1 <= N <= 1000).
Output
Results should be directed to standard output. The output of each test case should be a single real number, which is the mathematical expectation of the number of coins I have to donate. The result should be accurate to two digits after the fractional point.
Sample Input
2
1
2
Sample Output
1.00
2.50
該題目的思路很明確，就是概率題，嘗試了兩種解法，一種是用遞推，另一種是直接利用組合公式
遞推法：
//solution 1
以P[i][j]表示狀態(tài)， i代表A種面條剩下的數(shù)量，j代表B種面條的數(shù)量。
P[i][j] = P[i - 1][j] * 0.5 + P[i][j - 1] * 0.5 (i - 1 != 0 && j - 1 != 0, i為0或者j為0則為終結(jié)態(tài)）
Result =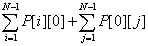 
#include <iostream>
#include <queue>
#include <cmath>
using namespace std;
#define MAXN 1100
double P[MAXN][MAXN];
double dVal;
double dResult[MAXN + 100];
int main()
{
int iCaseTimes;
int k, i, j;
double dVal;
scanf("%d", &iCaseTimes);
for(k = 0; k < iCaseTimes; k++)
{
scanf("%d", &iNum);
dRet = 0;
P[iNum + 1][iNum] = 1;
P[iNum][iNum + 1] = 1;
for(i = iNum; i >= 0; i--)
{
for(j = iNum; j >= 0; j--)
{
if(i + 1 >= 1 && j >= 1)
P[i][j] += P[i + 1][j] * 0.5;
if(i >= 1 && j + 1 >= 1)
P[i][j] += P[i][j + 1] * 0.5;
if(i == 0 || j == 0)
{
dRet += P[i][j] * (iNum * 2 - i - j);
}
}
}
printf("%.2lf\n", dRet);
}
return 0;
}
很明顯，算上總的Case數(shù)量，這種方法的時間復雜度為O(n^3), 所以，超時是必然的
這時轉(zhuǎn)換下思路，想想能不能一下子就把1000規(guī)模的打好表呢？在上述表示情況下，打表是不行的，因為每次進行計算的時候，都需要將P[iNum][iNum]
設置為概率1，所以，當直接打好1000的規(guī)模，其子問題仍然沒法計算出來。
//solution 2
換一狀態(tài)表示方法
我們令P[i][j]來代表狀態(tài)，其中的i, j代表A類面條吃了i碗，B類面條吃了j碗，這樣我們可以這樣得到答案：
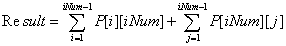
再觀察這時候的子結(jié)構(gòu)，假設先計算好規(guī)模為1000的表，此時的輸入為iNum，我們可以看到，到數(shù)量為iNum - 1的結(jié)果都是對的，而數(shù)量為iNum的結(jié)果
是錯誤的，因為1000大于iNum，在1000的規(guī)模下，到iNum時沒有進行終結(jié)，而當單類面條吃到iNum碗時，應該是結(jié)束態(tài)，所以，我們只能利用到規(guī)模為
iNum - 1數(shù)量的結(jié)果，并利用其推出最后答案。
//solution 1 O(n^2)
#include <iostream>
#include <cmath>
using namespace std;
#define MAXN 1100
double dRet[MAXN][MAXN];
int main()
{
int i, j;
int iNum, iCaseTimes;
double dResult;
memset(dRet, 0, sizeof(dRet));
dRet[0][0] = 1;
for(i = 0; i <= 1000; i++)
{
for(j = 0; j <= 1000; j++)
{
if(i == 0 && j == 0) continue;
if(i - 1 >= 0)
dRet[i][j] += dRet[i - 1][j] * 0.5;
if(j - 1 >= 0)
dRet[i][j] += dRet[i][j - 1] * 0.5;
//dRet[i][j] += 1;
}
}
scanf("%d", &iCaseTimes);
while(iCaseTimes--)
{
scanf("%d", &iNum);
dResult = 0;
for(i = 0; i <= iNum - 1; i++)
{
dResult += dRet[iNum - 1][i] * (iNum + i) * 0.5;
}
dResult *= 2;
printf("%.2lf\n", dResult);
}
return 0;
}
假如直接利用組合公式能否計算呢？
因為該事件發(fā)生的概率不是等可能事件，也就是說，假設有2 * iNum 碗面條，2 ^ (iNum + 1)并不是其樣本空間，因為其中一些序列是不可能發(fā)生的
那么假設拋硬幣事件一定發(fā)生（有點像條件概率,我具體想不明白:( ）， 那么，可以得到下面的公式：
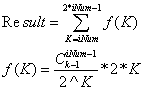
總的樣本空間為2^K，因為拋了K次硬幣，每次兩種選擇；而在這長度為K的串中，最后一碗必定是固定的（肯定為吃完的那種），
所以只要在剩下的K - 1碗中選出iNum - 1個位置便可。乘以二代表有兩類面條吃完的對稱情況，乘以K是轉(zhuǎn)換成期望。
//solution 2 O(n^2)
#include <iostream>
using namespace std;
#define MAXN 2100
double C[MAXN][MAXN - 1000];
int main()
{
int i, j;
memset(C, 0, sizeof(C));
C[0][0] = 0.5;
C[1][0] = 0.25;
C[1][1] = 0.25;
for(i = 2; i <= 2000; i++)
{
C[i][0] = C[i - 1][0] / 2.0;
for(j = 1; j <= 1000; j++)
{
C[i][j] = (C[i - 1][j] + C[i - 1][j - 1]) / 2.0;
}
}
int iNum;
int iN;
double dRetVal;
scanf("%d", &iNum);
while(iNum--)
{
scanf("%d", &iN);
dRetVal = 0;
for(i = iN; i <= iN * 2 - 1; i++)
{
dRetVal += C[i - 1][iN - 1] * i;
}
printf("%.2lf\n", dRetVal * 2);
}
return 0;
}
主要的思路是將組合數(shù)進行打表，更需要注意的是將2^k次也融入到整個組合數(shù)的表中，也就是說，在利用楊輝三角進行遞推的時候就將除二操作加進去。
這里要注意double類型的精度問題，由于題目只要求精確到小數(shù)兩位，所以利用double還是可以滿足的。
對于上述方法，雖然時間復雜度是O(n^2)，但是其空間復雜度也為O(n^2)，觀察到每兩個f(K)函數(shù)之間也有遞推關(guān)系，我們只要計算出第一個之后，再
乘上一個式子，除以一個式子，就可以得到下一個值，所以，再實現(xiàn)一個空間復雜度更小的O(n^2)的方法：
//solution 3
#include <iostream>
using namespace std;
int main()
{
int i, j;
int iNum;
int iN;
double dRetVal;
double dPreVal;
double dStartValue;
scanf("%d", &iNum);
while(iNum--)
{
scanf("%d", &iN);
dRetVal = 0;
dStartValue = 1;
//(iN - 1, iN - 1)
for(i = iN; i >= 1; i--) dStartValue /= 2.0;
dRetVal = dStartValue * iN;
dPreVal = dStartValue;
for(i = iN + 1; i <= iN * 2 - 1; i++)
{
dRetVal += (double) dPreVal * (i - 1) / (i - iN) * i / 2;
dPreVal = dPreVal * (i - 1) / ((i - iN) * 2);
}
printf("%.2lf\n", dRetVal * 2);
}
return 0;
}
通過對該題的解決，可以看到，概率類的題目基本上兩個方向：1.直接用組合公式解決。但是這種方法容易產(chǎn)生精度問題，而且不一定能夠簡單的推出來
2.用遞推公式解決。這種方法比較容易想清楚方法，但是面臨的問題便是時間與空間的限制。