題意:求一個n*n矩陣的最大子矩陣。
解題思路:類似一維情況下的最大連續子串。
代碼:
#include <cstdio>#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int maxn = 110;
int n, a[maxn][maxn], r[maxn][maxn] , f[maxn];
int main() {
while(~scanf("%d", &n)) {
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
scanf("%d", &a[i][j]);
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
r[i][j] = r[i-1][j] + a[i][j];
int ans = a[0][0];
for(int i=1;i<=n;i++)
for(int j=i;j<=n;j++)
for(int k=1;k<=n;k++) {
if(f[k-1] < 0) {
f[k] = r[j][k] - r[i-1][k];
} else {
f[k] = f[k-1] + r[j][k] - r[i-1][k];
}
if(f[k] > ans) ans = f[k];
}
printf("%d\n", ans);
}
return 0;
}
posted @
2015-03-31 23:15 JulyRina 閱讀(244) |
評論 (0) |
編輯 收藏
自動轉向(Auto-Redirecting),也叫自動重定向。自動跳轉,指當訪問用戶登陸到某網站時,自動將用戶轉向其它網頁地址的一種技術。轉向的網頁地址可以是網站內的其它網頁,也可以是其它網站。通常情況下,瀏覽器會收到一個網頁,該頁面含有自動加載一其它網頁的代碼。該頁面有可能在服務器端被轉換,這樣的話,瀏覽器只收到一個頁面,而自動轉向往往意味著瀏覽器收到的頁面具有自動將訪問用戶送至其它頁面的功能。
對自動轉向技術(Auto-Redirecting)的合理應用包括:將用戶轉向到指定瀏覽器的網頁版本;當網站的域名變更或刪除后將人們轉向到新域名 下,等等。但現在這種技術卻往往被搜索引擎優化人士用來作為提高網站的搜索引擎排名的一種手段。例如,先專門針對搜索引擎做一個高度優化的網頁,也就是我 們通常所說的“橋頁”,然后把這個網頁提交給搜索引擎來獲得好的排名。但是,當搜索用戶通過搜索引擎的搜索結果列表點擊該網頁列表進入后,將被自動轉向到 一個用戶本來無意去訪問的網站地址。搜索引擎常常認為自動轉向的網頁是對讀者的誤導,所以它會對這種網頁或網站施以懲戒,不過對一些自動轉向方法它目前還 無法自動檢測出來。
Meta Refresh Tag自動轉向法
由于搜索引擎能夠讀取HTML,而Meta tags也是HTML,所以對于這種自動轉向法,搜索引擎能夠自動檢測出來。因而無論網站的轉向出于什么目的,都很容易被搜索引擎視做對讀者的誤導而受到懲罰。不過,如果跳轉延遲時間設置合適,搜索引擎就不會視之為作弊。
頁面定時刷新元標識(Meta Refresh Tag)只能放在HTML代碼的< HEAD>區里。如下所示:
<meta http-equiv="refresh" content="10; url=http://www.baidu.com/">
其中的“10”是告訴瀏覽器在頁面加載5秒鐘后自動跳轉到url這個頁面。
這種方法常可以在論壇中見到。如果在論壇上發信息,先會看到一個確認頁面,幾秒后會自動重新跳轉回當前的論壇頁面中。
從搜索引擎優化的角度出發,一般不希望自動轉向有延遲。不過,如果是用Meta Refresh標識進行轉向,一定要注意把延遲時間設定成至少10秒以上。
“javascript”自動轉向法
由于不能解析javascript,所以搜索引擎無法察覺(自動檢測到)用javascript腳本進行的自動轉向。javascript自動重定向腳本可以放在網頁的任何位置上,如果要求立即跳轉,則可以將其放入網頁源碼的<head>區內的最上面。用javascript實現跳轉的范例如下:
<script language="javascript"><!--location.replace("pagename.html")//--></script>
其中的“pagename.html”指特定的重定向目標地址,用相對/絕對URL地址均可。
用javascript實現自動重定向的好處在于:用戶所訪問的目標URL不會保留在用戶瀏覽器的歷史記錄中,如果用戶按返回按鈕返回,則將回到跳轉前 的網頁,而不是包含javascript自動重定向腳本的跳轉頁面,所以不會出現當用戶點擊返回按鈕后返回至重定向頁,然后該頁自動跳轉到用戶本來想離開 的那個頁面的尷尬情形。
如果需要,可以把javascript自動重定向腳本存在一個外部文件中,并通過下面的命令行來加載,其中“filename.js”是該外部文件的路徑和文件名:
<script language="javascript" src="filename.js"></script>
注意:若需實現即刻轉向,或不希望人們看到轉向前的那個頁面,一般常用javascript腳本實現。在這種情況下應將javascript腳本放入HTML源碼的<HEAD>區中。
表單(FORM)自動轉向法
搜索引擎的“爬行”程序是不會填寫表單的,所以它們也不會注意到提交表單,因而可以利用表單來實現自動轉向(重定向)而不讓搜索引擎察覺。
對于表單,人們往往很少意識到:表單的Action參數中包含的URL地址其實正是瀏覽器向服務器所請求的URL。瀏覽器將會通過向請求的URL地址增 加一些格式為name=value的參數給予它以特殊的對待。在什么都沒有的情況下,瀏覽器仍舊會為該URL安排請求至服務器。
用javascript腳本可讓頁面開始加載時即提交表單。下面是一個用javascript實現表單自動提交,以及提交表單的范例:
<script language="javascript"><!--document.myform.submit()//--></script>
<form name="myform" action="pagename.html" method="get"></form>
其中“myform”可以是任意名稱,“pagename.html”用相對/絕對URL地址均可。
小結
如果訪問用戶最終看到的是他們想看到的,那么在搜索引擎優化中使用自動轉向技術并沒有什么不對,也并不是什么不道德的行為。但有些人往往會在利用“自動 跳轉”技術,利用“橋頁”吸引訪問者,然后把他們送到他們無意瀏覽的頁面或網站,這種做法只會引起訪問用戶的反感,又怎么能夠期望訪問流量可以有效轉化為最終客戶呢?
posted @
2015-03-17 09:07 JulyRina 閱讀(559) |
評論 (0) |
編輯 收藏
線程是有趣的
了解如何正確運用線程是每一個優秀程序員必備的素質。線程類似于進程。如同進程,線程由內核按時間分片進行管理。在單處理器系統中,內核使用時間分片來模擬線程的并發執行,這種方式和進程的相同。而在多處理器系統中,如同多個進程,線程實際上一樣可以并發執行。
那么為什么對于大多數合作性任務,多線程比多個獨立的進程更優越呢?這是因為,線程共享相同的內存空間。不同的線程可以存取內存中的同一個變量。所以,程序中的所有線程都可以讀或寫聲明過的全局變量。如果曾用 fork() 編寫過重要代碼,就會認識到這個工具的重要性。為什么呢?雖然 fork() 允許創建多個進程,但它還會帶來以下通信問題: 如何讓多個進程相互通信,這里每個進程都有各自獨立的內存空間。對這個問題沒有一個簡單的答案。雖然有許多不同種類的本地 IPC (進程間通信),但它們都遇到兩個重要障礙:
- 強加了某種形式的額外內核開銷,從而降低性能。
- 對于大多數情形,IPC 不是對于代碼的“自然”擴展。通常極大地增加了程序的復雜性。
雙重壞事: 開銷和復雜性都非好事。如果曾經為了支持 IPC 而對程序大動干戈過,那么您就會真正欣賞線程提供的簡單共享內存機制。由于所有的線程都駐留在同一內存空間,POSIX 線程無需進行開銷大而復雜的長距離調用。只要利用簡單的同步機制,程序中所有的線程都可以讀取和修改已有的數據結構。而無需將數據經由文件描述符轉儲或擠入緊窄的共享內存空間。僅此一個原因,就足以讓您考慮應該采用單進程/多線程模式而非多進程/單線程模式。
線程是快捷的
不僅如此。線程同樣還是非常快捷的。與標準 fork() 相比,線程帶來的開銷很小。內核無需單獨復制進程的內存空間或文件描述符等等。這就節省了大量的 CPU 時間,使得線程創建比新進程創建快上十到一百倍。因為這一點,可以大量使用線程而無需太過于擔心帶來的 CPU 或內存不足。使用 fork() 時導致的大量 CPU 占用也不復存在。這表示只要在程序中有意義,通常就可以創建線程。
當然,和進程一樣,線程將利用多 CPU。如果軟件是針對多處理器系統設計的,這就真的是一大特性(如果軟件是開放源碼,則最終可能在不少平臺上運行)。特定類型線程程序(尤其是 CPU 密集型程序)的性能將隨系統中處理器的數目幾乎線性地提高。如果正在編寫 CPU 非常密集型的程序,則絕對想設法在代碼中使用多線程。一旦掌握了線程編碼,無需使用繁瑣的 IPC 和其它復雜的通信機制,就能夠以全新和創造性的方法解決編碼難題。所有這些特性配合在一起使得多線程編程更有趣、快速和靈活。
線程是可移植的
如果熟悉 Linux 編程,就有可能知道 __clone() 系統調用。__clone() 類似于 fork(),同時也有許多線程的特性。例如,使用 __clone(),新的子進程可以有選擇地共享父進程的執行環境(內存空間,文件描述符等)。這是好的一面。但 __clone() 也有不足之處。正如__clone() 在線幫助指出:
“__clone 調用是特定于 Linux 平臺的,不適用于實現可移植的程序。欲編寫線程化應用程序(多線程控制同一內存空間),最好使用實現 POSIX 1003.1c 線程 API 的庫,例如 Linux-Threads 庫。參閱 pthread_create(3thr)。”
雖然 __clone() 有線程的許多特性,但它是不可移植的。當然這并不意味著代碼中不能使用它。但在軟件中考慮使用 __clone() 時應當權衡這一事實。值得慶幸的是,正如 __clone() 在線幫助指出,有一種更好的替代方案:POSIX 線程。如果想編寫
可移植的 多線程代碼,代碼可運行于 Solaris、FreeBSD、Linux 和其它平臺,POSIX 線程是一種當然之選。
第一個線程
下面是一個 POSIX 線程的簡單示例程序:
#include <pthread.h>
#include <stdlib.h>
#include <unistd.h>
void *thread_function(void *arg) {
int i;
for ( i=0; i<20; i++) {
printf("Thread says hi!\n");
sleep(1);
}
return NULL;
}
int main(void) {
pthread_t mythread;
if ( pthread_create( &mythread, NULL, thread_function, NULL) ) {
printf("error creating thread.");
abort();
}
if ( pthread_join ( mythread, NULL ) ) {
printf("error joining thread.");
abort();
}
exit(0);
}
要編譯這個程序,只需先將程序存為 thread1.c,然后輸入:
$ gcc thread1.c -o thread1 -lpthread
運行則輸入:
$ ./thread1
理解 thread1.c
thread1.c 是一個非常簡單的線程程序。雖然它沒有實現什么有用的功能,但可以幫助理解線程的運行機制。下面,我們一步一步地了解這個程序是干什么的。main() 中聲明了變量 mythread,類型是 pthread_t。pthread_t 類型在 pthread.h 中定義,通常稱為“線程 id”(縮寫為 "tid")。可以認為它是一種線程句柄。
mythread 聲明后(記住 mythread 只是一個 "tid",或是將要創建的線程的句柄),調用 pthread_create 函數創建一個真實活動的線程。不要因為 pthread_create() 在 "if" 語句內而受其迷惑。由于 pthread_create() 執行成功時返回零而失敗時則返回非零值,將 pthread_create() 函數調用放在 if() 語句中只是為了方便地檢測失敗的調用。讓我們查看一下 pthread_create 參數。第一個參數 &mythread 是指向 mythread 的指針。第二個參數當前為 NULL,可用來定義線程的某些屬性。由于缺省的線程屬性是適用的,只需將該參數設為 NULL。
第三個參數是新線程啟動時調用的函數名。本例中,函數名為 thread_function()。當 thread_function() 返回時,新線程將終止。本例中,線程函數沒有實現大的功能。它僅將 "Thread says hi!" 輸出 20 次然后退出。注意 thread_function() 接受 void * 作為參數,同時返回值的類型也是 void *。這表明可以用 void * 向新線程傳遞任意類型的數據,新線程完成時也可返回任意類型的數據。那如何向線程傳遞一個任意參數?很簡單。只要利用 pthread_create() 中的第四個參數。本例中,因為沒有必要將任何數據傳給微不足道的 thread_function(),所以將第四個參數設為 NULL。
您也許已推測到,在 pthread_create() 成功返回之后,程序將包含兩個線程。等一等, 兩個 線程?我們不是只創建了一個線程嗎?不錯,我們只創建了一個進程。但是主程序同樣也是一個線程。可以這樣理解:如果編寫的程序根本沒有使用 POSIX 線程,則該程序是單線程的(這個單線程稱為“主”線程)。創建一個新線程之后程序總共就有兩個線程了。
我想此時您至少有兩個重要問題。第一個問題,新線程創建之后主線程如何運行。答案,主線程按順序繼續執行下一行程序(本例中執行 "if (pthread_join(...))")。第二個問題,新線程結束時如何處理。答案,新線程先停止,然后作為其清理過程的一部分,等待與另一個線程合并或“連接”。
現在,來看一下 pthread_join()。正如 pthread_create() 將一個線程拆分為兩個, pthread_join() 將兩個線程合并為一個線程。pthread_join() 的第一個參數是 tid mythread。第二個參數是指向 void 指針的指針。如果 void 指針不為 NULL,pthread_join 將線程的 void * 返回值放置在指定的位置上。由于我們不必理會 thread_function() 的返回值,所以將其設為 NULL.
您會注意到 thread_function() 花了 20 秒才完成。在 thread_function() 結束很久之前,主線程就已經調用了 pthread_join()。如果發生這種情況,主線程將中斷(轉向睡眠)然后等待 thread_function() 完成。當 thread_function() 完成后, pthread_join() 將返回。這時程序又只有一個主線程。當程序退出時,所有新線程已經使用 pthread_join() 合并了。這就是應該如何處理在程序中創建的每個新線程的過程。如果沒有合并一個新線程,則它仍然對系統的最大線程數限制不利。這意味著如果未對線程做正確的清理,最終會導致 pthread_create() 調用失敗。
無父,無子
如果使用過 fork() 系統調用,可能熟悉父進程和子進程的概念。當用 fork() 創建另一個新進程時,新進程是子進程,原始進程是父進程。這創建了可能非常有用的層次關系,尤其是等待子進程終止時。例如,waitpid() 函數讓當前進程等待所有子進程終止。waitpid() 用來在父進程中實現簡單的清理過程。
而 POSIX 線程就更有意思。您可能已經注意到我一直有意避免使用“父線程”和“子線程”的說法。這是因為 POSIX 線程中不存在這種層次關系。雖然主線程可以創建一個新線程,新線程可以創建另一個新線程,POSIX 線程標準將它們視為等同的層次。所以等待子線程退出的概念在這里沒有意義。POSIX 線程標準不記錄任何“家族”信息。缺少家族信息有一個主要含意:如果要等待一個線程終止,就必須將線程的 tid 傳遞給 pthread_join()。線程庫無法為您斷定 tid。
對大多數開發者來說這不是個好消息,因為這會使有多個線程的程序復雜化。不過不要為此擔憂。POSIX 線程標準提供了有效地管理多個線程所需要的所有工具。實際上,沒有父/子關系這一事實卻為在程序中使用線程開辟了更創造性的方法。例如,如果有一個線程稱為線程 1,線程 1 創建了稱為線程 2 的線程,則線程 1 自己沒有必要調用 pthread_join() 來合并線程 2,程序中其它任一線程都可以做到。當編寫大量使用線程的代碼時,這就可能允許發生有趣的事情。例如,可以創建一個包含所有已停止線程的全局“死線程列表”,然后讓一個專門的清理線程專等停止的線程加到列表中。這個清理線程調用 pthread_join() 將剛停止的線程與自己合并。現在,僅用一個線程就巧妙和有效地處理了全部清理。
更多資料
posted @
2015-03-16 21:18 JulyRina 閱讀(263) |
評論 (0) |
編輯 收藏
下圖很好的概括了ClamAV的運行流程。
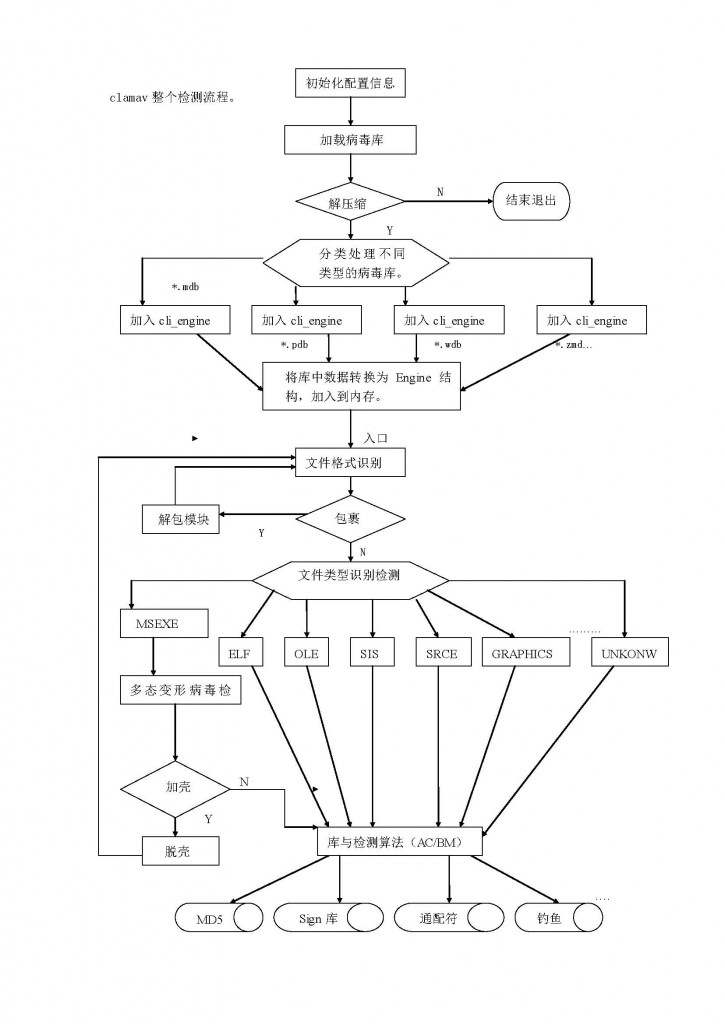
posted @
2015-03-09 23:14 JulyRina 閱讀(964) |
評論 (0) |
編輯 收藏ClamAV 簡介以及適用范圍
ClamAV是一個在命令行下查毒軟件,因為它不將殺毒作為主要功能,默認只能查出您計算機內的病毒,但是無法清除,至多刪除文件。ClamAV可以工作很多的平臺上,但是有少數無法支持,這就要取決您所使用的平臺的流行程度了。另外它主要是來防護一些WINDOWS病毒和木馬程序。另外,這是一個面向服務端的軟件。
需要反病毒軟件?免費么?
絕大多數的Linux都是很先進的,所以,很少有病毒能夠在linux上運行和繁衍。而且,由于目前PC都使用的是Windows,所以病毒制造者們更愿意去寫Windows下的病毒。但是還有很多的原因能致使您使用一些病毒掃描程序的,比如:
- 掃描在您計算機上的Windows設備
- 掃描在本地網絡中的Windows計算機
- 掃描您即將要傳送給別人的文件
- 掃描您將要發送給別人的EMAIL
ClamAV 安裝設置
安裝ClamAV
sudo apt-get install clamav
這里有兩種的ClamAV供您選擇 1.手動:安裝ClamAV的安裝包 2.自動:安裝ClamAV-daemon 這兩種都可以安裝ClamAV,但是要是使用上面的方法,是手動的。 在您安裝完成之后,您可能被程序問及一些問題,比如怎么去升級。這就需要您選擇一個離您比較近的服務器來升級。ClamAV的升級程序是很小的,所以很值得去自動升級。
怎么使用ClamAV
這部分將會介紹安裝之后的使用
升級我的病毒庫
運行 sudo freshclam.
您將會看見以下說明
user@ubuntu:/etc/clamav # sudo freshclam
ClamAV update process started at Wed Apr 27 00:06:47 2005
main.cvd is up to date (version: 31, sigs: 33079, f-level: 4, builder: tkojm)
daily.cvd is up to date (version: 855, sigs: 714, f-level: 4, builder: ccordes)
使用ClamAV掃描我計算機中的文件
運行 clamscan.
這里附帶一些例子
- 掃描所有用戶的主目錄就使用 clamscan -r /home
- 掃描您計算機上的所有文件并且顯示所有的文件的掃描結果,就使用 clamscan -r /
- 掃描您計算機上的所有文件并且顯示有問題的文件的掃描結果, 就使用 clamscan -r --bell -i /
- 當clamAV掃描完所有文件的時候,會顯示如下的類似報告
ClamAV只會去掃描對于ClamAV可以讀取的文件。 如果您想掃描所有文件,在命令前加上 sudo .
使ClamAV以daemon防護的方式運行
安裝clamav-daemon就可以了,clamav-daemon將會建立一個名為'clamav'的帳戶,這是為了可以使ClamAV掃描一些系統文件,比如您的Email存放的地方,您可以添加'clamav'為這些文件或者目錄的所有者。
如何知道clamav-daemon是否運行了?
查看進程列表就可以了:
ps ax | grep [c]lamd
如何刪除病毒文件?
在掃描的時候,您可以添加'--remove'
如何知道我現在使用的ClamAV版本?
執行 clamscan -V
如何使ClamAV按計劃自動運行
您可以使用'at'命令來使clamscan和freshclam運行,比如
at 3:30 tomorrow
at>clamscan -i /home/user > mail user@example.com
at> <CTRL-D>
job 3 at 2015-03-10 03:30
或者編輯 /etc/crontab 加入以下內容
0 3 * * * root /usr/bin/freshclam --quiet -l /var/log/clamav/clamav.log ##每天3點升級
更多內容請參見
Ubuntu中文社區ClamAV專欄。
posted @
2015-03-09 19:41 JulyRina 閱讀(651) |
評論 (0) |
編輯 收藏
問題來自于一場“3分鐘相親”活動,參加活動的有n位男士和n位女士。要求每位男士都要和所有的女士進行短暫的單獨交流,并為她們打分,然后按照喜歡程度,對每一位女士進行排序;同樣的,每位女士也要對所有男士進行打分和排序。
在這之后我們為選擇策略為這n位男士和n位女士配對。使得在婚后不會有“出軌”的情況發生。
這里的“出軌”是什么意思:
圖片來自網絡,僅作舉例之用

如果以下兩種情況之一發生,則會發生出軌:
- 如果第一對夫妻中的妻子在婚后覺得自己的丈夫沒有第二對夫妻中的丈夫帥;第二對夫妻中的丈夫同樣也覺得自己的妻子沒有第一對夫妻中的妻子漂亮
- 如果第一對夫妻中的丈夫在婚后覺得自己的妻子沒有第二對夫妻中的妻子美;第二對夫妻中的妻子同樣也覺得自己的丈夫沒有第一對夫妻中的丈夫帥
解決穩定婚姻的算法之一:
延遲認可算法(Gale-Shapley算法)
先對所有男士進行落選標記,稱其為自由男。當存在自由男時,進行以下操作:
- 每一位自由男在所有尚未拒絕她的女士中選擇一位被他排名最優先的女士;
- 每一位女士將正在追求她的自由男與其當前男友進行比較,選擇其中排名優先的男士作為其男友,即若自由男優于當前男友,則拋棄前男友;否則保留其男友,拒絕自由男。
- 若某男士被其女友拋棄,重新變成自由男。
在算法執行期間,自由男們
主動出擊,依次對最喜歡和次喜歡的女人求愛,一旦被接受,即失去自由身,進入訂婚狀態;而女人們則采取
“守株待兔”和
“喜新厭舊”策略,對前來求愛的男士進行選擇:若該男子比未婚夫強,則悔婚,選擇新的未婚夫;否則拒絕該男子的求婚。被女友拋棄的男人重獲自由身,重新擁有了追求女人的權利——當然,新的追求對象比不過前女友。
這樣,在算法執行期間,每個人都有可能訂婚多次——也有可能一開始就找到了自己的最愛,從一而終——每訂一次婚,女人們的選擇就會更有利,而男人們的品味則越來越差。只要男女生的數量相等,則經過多輪求婚,訂婚,悔婚和再訂婚之后,每位男女最終都會找到合適的伴侶——雖然不一定是自己的最愛(男人沒能追到自己的最愛,或女人沒有等到自己的最愛來追求),但絕對不會出現“雖然彼此相愛,卻不能在一起”的悲劇,所有人都會組成穩定的婚姻。
posted @
2015-03-09 18:57 JulyRina 閱讀(362) |
評論 (0) |
編輯 收藏
字典樹是一種樹形數據結構,他有如下特點:
每個節點都有固定個數的指向兒子節點的指針,她的兒子某一個節點(如果存在的話)包含的信息就是該節點的下一個字符。
根節點不包含字符,除根節點外每一個節點都只包含一個字符; 從根節點到某一節點,路徑上經過的字符連接起來,為該節點對應的字符串; 每個節點的所有子節點包含的字符都不相同。
例:作為一個簡單的演示,這里我們稍微忽略一些細節。下面的這棵樹就是一個簡單的
字典樹的例子:

如圖所示,如果我們按行存儲這些數據:
apple
append
and
antiy
banana
band
我們需要5+6+3+5+6+4=29 B 的空間。
但是字典樹只需要20 B 的空間。
這在數據量更大的時候能起到更好的效果。
字典樹能夠線性時間范圍內實現數據的增刪改查。
posted @
2015-03-09 18:55 JulyRina 閱讀(349) |
評論 (0) |
編輯 收藏
【練習】
2.3-2 MERGE的改進
void MERGE(int *A, int p,int q, int r) {
int B[maxn] , i = p , j = q+1 , k = 0;
while(k < r - p + 1) {
if(i > q || j <= r && A[i] > A[j]) B[k++] = A[j++];
else B[k++] = A[i++];
}
for(i=0;i<r-p+1;i++) A[p+i] = B[i];
}
2.3-5 二分查找的C++代碼
int find(int *a, int l, int r, int value) {
if(l == r) return l;
int mid = (l+r) >> 1;
if(a[mid] >= value) return find(a, l, mid, value);
else return find(a , mid+1, r , value);
}
*2.3-7 (這道題其實有O(n)的算法,而且寫起來更方便些)這里是O(nlogn)的算法
O(nlogn)算法思想:1.首先進行排序;2.然后枚舉每一個小于等于x/2的數S[i],二分查找對應的x-S[i]是否存在
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int maxn = 1010;
bool findx(int *S,int n, int x,int l,int r) {
if(l > r) return false;
if(l ==r) return S[l] == x;
int mid = (l+r) >> 1;
if(S[mid] >= x) return findx(S, n, x, l, mid);
else return findx(S, n, x, mid+1, r);
}
bool check(int *S,int n,int x) {
for(int i=0;S[i]<=x/2 && i < n;i++) {
if(findx(S, n, x-S[i], i+1, n-1)) return true;
}
return false;
}
int main() {
int S[1010] , x , n;
while(~scanf("%d%d" , &n , &x)) {
for(int i=0;i<n;i++) cin >> S[i];
if(check(S, n, x)) puts("yes");
else puts("no");
}
return 0;
}
O(n)的方法是在數的范圍不是特別大的時候(或者數的范圍比較大,此時采用hash的方法)標記的方法,這里假設數的范圍<=10000,并且假設數沒有重復的情況下,其他情況稍許改變一下就行:
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int maxn = 1010;
bool check(int *S,int n,int x) {
bool vis[10001] = {0};
for(int i=0;i<n;i++) vis[x-S[i]] = true;
for(int i=0;i<n;i++) if(vis[S[i]]) return true;
return false;
}
int n ,x , S[maxn];
int main() {
while(~scanf("%d%d" , &n , &x)) {
for(int i=0;i<n;i++) cin >> S[i];
if(check(S, n, x)) puts("yes");
else puts("no");
}
return 0;
}
2-4(逆序對):這道題就是在歸并排序中得到逆序對,具體見代碼:
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int maxn = 1010;
int ans;
void merge_sort(int *A, int l,int r) {
if(l >= r) return;
int mid = (l+r) >> 1;
merge_sort(A, l, mid);
merge_sort(A, mid+1, r);
int i = l , j = mid+1 ,B[maxn] , k = l;
while(i <= mid || j <= r) {
if(i > mid || j <= r && A[j] < A[i]) B[k++] = A[j++] , ans += mid-i+1;
else B[k++] = A[i++];
}
for(i=l;i<=r;i++) A[i] = B[i];
}
int main() {
int A[maxn] , n;
while(~scanf("%d" , &n)) {
for(int i=0;i<n;i++) cin >> A[i];
ans = 0;
merge_sort(A, 0, n-1);
cout << ans << endl;
//for(int i=0;i<n;i++) cout << A[i] << " "; cout << endl;
}
return 0;
}
posted @
2015-03-07 15:19 JulyRina 閱讀(323) |
評論 (0) |
編輯 收藏
(一)巴什博奕(Bash Game):只有一堆n個物品,兩個人輪流從這堆物品中取物,規定每次至少取一個,最多取m個。最后取光者得勝。
顯然,如果n=m+1,那么由于一次最多只能取m個,所以,無論先取者拿走多少個,后取者都能夠一次拿走剩余的物品,后者取勝。因此我們發現了如何取勝的法則:如果n=(m+1)r+s,(r為任意自然數,s≤m),那么先取者要拿走s個物品,如果后取者拿走k(≤m)個,那么先取者再拿走m+1-k個,結果剩下(m+1)(r-1)個,以后保持這樣的取法,那么先取者肯定獲勝。總之,要保持給對手留下(m+1)的倍數,就能最后獲勝。
即,若n=k*(m+1),則后取著勝,反之,存在先取者獲勝的取法。
n%(m+1)==0. 先取者必敗。
(二)威佐夫博奕(Wythoff Game):有兩堆各若干個物品,兩個人輪流從某一堆或同時從兩堆中取同樣多的物品,規定每次至少取一個,多者不限,最后取光者得勝。
這種情況下是頗為復雜的。我們用(ak,bk)(ak ≤ bk ,k=0,1,2,...,n)表示兩堆物品的數量并稱其為局勢,如果甲面對(0,0),那么甲已經輸了,這種局勢我們稱為奇異局勢。前幾個奇異局勢是:(0,0)、(1,2)、(3,5)、(4,7)、(6,10)、(8,13)、(9,15)、(11,18)、(12,20)。
可以看出,a0=b0=0,ak是未在前面出現過的最小自然數,而 bk= ak + k,奇異局勢有
如下三條性質:
1。任何自然數都包含在一個且僅有一個奇異局勢中。
由于ak是未在前面出現過的最小自然數,所以有ak > ak-1 ,而 bk= ak + k > ak-1 + k-1 = bk-1 > ak-1 。所以性質1。成立。
2。任意操作都可將奇異局勢變為非奇異局勢。
事實上,若只改變奇異局勢(ak,bk)的某一個分量,那么另一個分量不可能在其他奇異局勢中,所以必然是非奇異局勢。如果使(ak,bk)的兩個分量同時減少,則由于其差不變,且不可能是其他奇異局勢的差,因此也是非奇異局勢。
3。采用適當的方法,可以將非奇異局勢變為奇異局勢。
假設面對的局勢是(a,b),若 b = a,則同時從兩堆中取走 a 個物體,就變為了奇異局勢(0,0);如果a = ak ,b > bk,那么,取走b - bk個物體,即變為奇異局勢;如果 a = ak , b < bk ,則同時從兩堆中拿走 ak - ab - ak個物體,變為奇異局勢( ab - ak , ab - ak+ b - ak);如果a > ak ,b= ak + k,則從第一堆中拿走多余的數量a - ak 即可;如果a < ak ,b= ak + k,分兩種情況,第一種,a=aj (j < k),從第二堆里面拿走 b - bj 即可;第二種,a=bj (j < k),從第二堆里面拿走 b - aj 即可。
從如上性質可知,兩個人如果都采用正確操作,那么面對非奇異局勢,先拿者必勝;反之,則后拿者取勝。
那么任給一個局勢(a,b),怎樣判斷它是不是奇異局勢呢?我們有如下公式:
ak =[k(1+√5)/2],bk= ak + k (k=0,1,2,...,n 方括號表示取整函數)
奇妙的是其中出現了黃金分割數(1+√5)/2 = 1。618...,因此,由ak,bk組成的矩形近似為黃金矩形,由于2/(1+√5)=(√5-1)/2,可以先求出j=[a(√5-1)/2],若a=[j(1+√5)/2],那么a = aj,bj = aj + j,若不等于,那么a = aj+1,bj+1 = aj+1+ j + 1,若都不是,那么就不是奇異局勢。然后再按照上述法則進行,一定會遇到奇異局勢。
(三)尼姆博奕(Nimm Game):有三堆各若干個物品,兩個人輪流從某一堆取任意多的物品,規定每次至少取一個,多者不限,最后取光者得勝。
這種情況最有意思,它與二進制有密切關系,我們用(a,b,c)表示某種局勢,首先(0,0,0)顯然是奇異局勢,無論誰面對奇異局勢,都必然失敗。第二種奇異局勢是(0,n,n),只要與對手拿走一樣多的物品,最后都將導致(0,0,0)。仔細分析一下,(1,2,3)也是奇異局勢,無論對手如何拿,接下來都可以變為(0,n,n)的情形。
計算機算法里面有一種叫做按位模2加,也叫做異或的運算,我們用符號(^)表示這種運算。這種運算和一般加法不同的一點是1^1=0。先看(1,2,3)的按位模2加的結果:
1 =二進制01
2 =二進制10
3 =二進制11 (^)
———————
0 =二進制00 (注意不進位)
對于奇異局勢(0,n,n)也一樣,結果也是0。
任何奇異局勢(a,b,c)都有a(^)b(^)c =0。
如果我們面對的是一個非奇異局勢(a,b,c),要如何變為奇異局勢呢?假設 a < b < c,我們只要將 c 變為 a(^)b,即可,因為有如下的運算結果: a(^)b(^)(a(^)b)=(a(^)a)(^)(b(^)b)=0(^)0=0。要將c 變為a(^)b,只要從 c中減去 c-(a(^)b)即可。
獲勝情況對先取者進行討論:
異或結果為0,先取者必敗,無獲勝方法。后取者獲勝;
結果不為0,先取者有獲勝的取法。
拓展: 任給N堆石子,兩人輪流從任一堆中任取(每次只能取自一堆),取最后一顆石子的人獲勝,問先取的人如何獲勝?
根據上面所述,N個數異或即可。如果開始的時候T=0,那么先取者必敗,如果開始的時候T>0,那么只要每次取出石子使得T=0,即先取者有獲勝的方法。
posted @
2015-03-04 11:16 JulyRina 閱讀(320) |
評論 (1) |
編輯 收藏
題目
有N種物品和一個容量為V的背包。第i種物品最多有n[i]件可用,每件費用是c[i],價值是w[i]。求解將哪些物品裝入背包可使這些物品的費用總和不超過背包容量,且價值總和最大。
基本算法
這題目和完全背包問題很類似。基本的方程只需將完全背包問題的方程略微一改即可,因為對于第i種物品有n[i]+1種策略:取0件,取1件……取n[i]件。令f[i][v]表示前i種物品恰放入一個容量為v的背包的最大權值,則有狀態轉移方程:
f[i][v]=max{f[i-1][v-k*c[i]]+k*w[i]|0<=k<=n[i]}
復雜度是O(V*Σn[i])。
轉化為01背包問題
另一種好想好寫的基本方法是轉化為01背包求解:把第i種物品換成n[i]件01背包中的物品,則得到了物品數為Σn[i]的01背包問題,直接求解,復雜度仍然是O(V*Σn[i])。
但是我們期望將它轉化為01背包問題之后能夠像完全背包一樣降低復雜度。仍然考慮二進制的思想,我們考慮把第i種物品換成若干件物品,使得原問題中第i種物品可取的每種策略——取0..n[i]件——均能等價于取若干件代換以后的物品。另外,取超過n[i]件的策略必不能出現。
方法是:將第i種物品分成若干件物品,其中每件物品有一個系數,這件物品的費用和價值均是原來的費用和價值乘以這個系數。使這些系數分別為1,2,4,...,2^(k-1),n[i]-2^k+1,且k是滿足n[i]-2^k+1>0的最大整數。例如,如果n[i]為13,就將這種物品分成系數分別為1,2,4,6的四件物品。
分成的這幾件物品的系數和為n[i],表明不可能取多于n[i]件的第i種物品。另外這種方法也能保證對于0..n[i]間的每一個整數,均可以用若干個系數的和表示,這個證明可以分0..2^k-1和2^k..n[i]兩段來分別討論得出,并不難,希望你自己思考嘗試一下。
這樣就將第i種物品分成了O(log n[i])種物品,將原問題轉化為了復雜度為<math>O(V*Σlog n[i])的01背包問題,是很大的改進。
下面給出O(log amount)時間處理一件多重背包中物品的過程,其中amount表示物品的數量:
procedure MultiplePack(cost,weight,amount)
if cost*amount>=V
CompletePack(cost,weight)
return
integer k=1
while k<amount
ZeroOnePack(k*cost,k*weight)
amount=amount-k
k=k*2
ZeroOnePack(amount*cost,amount*weight)
希望你仔細體會這個偽代碼,如果不太理解的話,不妨翻譯成程序代碼以后,單步執行幾次,或者頭腦加紙筆模擬一下,也許就會慢慢理解了。
O(VN)的算法
多重背包問題同樣有O(VN)的算法。這個算法基于基本算法的狀態轉移方程,但應用單調隊列的方法使每個狀態的值可以以均攤O(1)的時間求解。由于用單調隊列優化的DP已超出了NOIP的范圍,故本文不再展開講解。我最初了解到這個方法是在樓天成的“男人八題”幻燈片上。
小結
這里我們看到了將一個算法的復雜度由O(V*Σn[i])改進到O(V*Σlog n[i])的過程,還知道了存在應用超出NOIP范圍的知識的O(VN)算法。希望你特別注意“拆分物品”的思想和方法,自己證明一下它的正確性,并將完整的程序代碼寫出來。
posted @
2015-02-18 20:33 JulyRina 閱讀(406) |
評論 (0) |
編輯 收藏