µÅÅĶ┐░ÕQ?/strong>Õ£©Õ»╣õ║ÄõōQķĆēõĖĆõĖ¬ÕøŠõĖŁń╗ōńé╣õžō(f©┤)µĀ╣ńÜäDFSµÉ£ńā”(ch©│)µĀ?w©©i)õĖŁÕ╗║ń½ŗõĖĆõĖ¬LABµĢ░ń╗äõĖÄLOWµĢ░ń╗äÕQīLABµĢ░ń╗äÕŁśÕé©õĖ¬ń╗ōńé╣ńÜäŠ~¢ÕÅĘÕQīLOWµĢ░ń╗äÕŁśÕé©ÕÉäńé╣ÕÅ?qi©óng)ÕģČÕŁÉµĀ?w©©i)ńÜäÕÉäŠlōńé╣ĶāĮÕł░ĶŠäĪÜäµ£Ć׫Åń╝¢ÕÅ’L(f©źng)╗ōńé╣ńÜäŠ~¢ÕÅĘŃĆ?br>
2 DFS(u)
3 LAB[u] = LOW[u] = lab++
4 for each (u, v) in E(G)
5 if LAB[v] is 0
6 DFS(v)
7 LOW[u] = min{LOW[u], LOW[v]}
8 else if v isnot parent of u
9 LOW[u] = min{LOW[u], LAB[v]}
ĮW?ĶĪīõĖŁÕQīÕ”éµ×?u, v)µś»µĀæ(w©©i)ĶŠ╣’╝īÕłÖÕ»╣vÕüܵĘ▒Õ║”õ╝śÕģłµÉ£ń┤ó’╝ī“qČõĖöLOW[u] = min{LOW[u], LOW[v]}ÕQīÕ”éµ×?u, v)µś»ÕÅŹÕÉæĶŠ╣ÕQīÕłÖLOW[u] = min{LOW[u], LAB[v]}ŃĆ?/span>
õĖēŃĆüÕē▓ńé?br> µÅÅĶ┐░ÕQ?/strong>ÕĮōõĖĆõĖ¬ń╗ōńé╣uµś»Õē▓ńéęÄ(gu©®)ŚČÕ┐ģµ╗ĪŁæ│õ╗źõĖŗõĖżõĖ¬µØĪõ╗Čõ╣ŗõĖĆÕQ?br> 1ÕQēuõĖ║µĀ╣õĖöĶć│׫浣ēõĖżµŻĄÕŁÉµĀæ(w©©i)ÕQ?br> 2ÕQēuõĖŹõžō(f©┤)µĀ╣õĖöÕŁśÕ£©õĖĆõĖ¬uÕ£©µĘ▒µÉ£µĀæ(w©©i)õĖŁńÜäÕŁÉÕź│võĮ┐ÕŠŚLOW[v] ≥ LAB[u]ŃĆ?br> ĮC▐ZŠŗÕQ?/strong>POJ 1523 Ķ¦ŻķóśµŖźÕæŖŃĆ?br>ÕøøŃĆüµĪź
µÅÅĶ┐░ÕQ?/strong>õĖƵØĪĶŠ╣e=(u, v)µś»µĪźÕQīÕĮōõĖöõ╗ģÕĮōeõĖ║µĀæ(w©©i)µ×ØĶŠ╣õĖöLOW[v] > LAB[u]ŃĆ?br> ĮC▐ZŠŗÕQ?/strong>POJ 3352 Ķ¦ŻķóśµŖźÕæŖŃĆ?/span>
Description
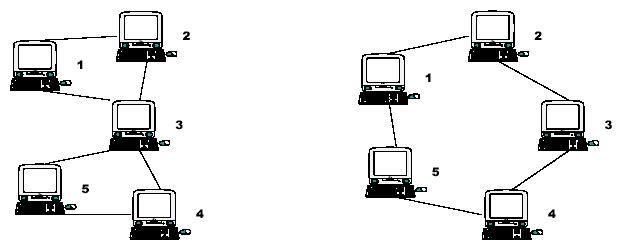
Node 3 is therefore a Single Point of Failure (SPF) for this network. Strictly, an SPF will be defined as any node that, if unavailable, would prevent at least one pair of available nodes from being able to communicate on what was previously a fully connected network. Note that the network on the right has no such node; there is no SPF in the network. At least two machines must fail before there are any pairs of available nodes which cannot communicate.
Input
Output
The first network in the file should be identified as "Network #1", the second as "Network #2", etc. For each SPF node, output a line, formatted as shown in the examples below, that identifies the node and the number of fully connected subnets that remain when that node fails. If the network has no SPF nodes, simply output the text "No SPF nodes" instead of a list of SPF nodes.
Sample Input
1 2 5 4 3 1 3 2 3 4 3 5 0 1 2 2 3 3 4 4 5 5 1 0 1 2 2 3 3 4 4 6 6 3 2 5 5 1 0 0
Sample Output
Network #1 SPF node 3 leaves 2 subnets Network #2 No SPF nodes Network #3 SPF node 2 leaves 2 subnets SPF node 3 leaves 2 subnets
õ║īŃĆüÕłåµ×?br> ńö©DFSĶ¦ŻÕå│ķŚ«ķóśÕQīĶ»”Šlåń«Śµ│Ģ’╝Ü(x©¼)Õē▓ńé╣õĖĵĪźŃĆ?/span>
õĖēŃĆüõ╗ŻńĀ?br>
 #include<iostream>
#include<iostream>2
 #include<list>
#include<list>3
 using namespace std;
using namespace std;4
 int t;
int t;5
 int v1, v2;
int v1, v2;6
 list<int> g[1001];
list<int> g[1001];7
 bool flag;
bool flag;8
 int root;
int root;9
 int counter;
int counter;10
 bool spf[1001];
bool spf[1001];11
 int low[1001], lab[1001];
int low[1001], lab[1001];12
 bool visit[1001];
bool visit[1001];13
 void dfs(int u, int fa)
void dfs(int u, int fa)14


 {
{15
 low[u] = lab[u] = counter++;
low[u] = lab[u] = counter++;16
 list<int>::iterator it;
list<int>::iterator it;17
 int counter = 0;
int counter = 0;18
 for(it = g[u].begin(); it != g[u].end(); it++)
for(it = g[u].begin(); it != g[u].end(); it++)19


 {
{20
 int v = *it;
int v = *it;21
 if(!lab[v])
if(!lab[v])22


 {
{23
 counter++;
counter++;24
 dfs(v, u);
dfs(v, u);25
 low[u] = min(low[u], low[v]);
low[u] = min(low[u], low[v]);26
 if((u==root && counter>=2) || (u!=root && low[v]>=lab[u]))
if((u==root && counter>=2) || (u!=root && low[v]>=lab[u]))27
 spf[u] = flag = true;
spf[u] = flag = true;28
 }
}29
 else if(v != fa)
else if(v != fa)30
 low[u] = min(low[u], lab[v]);
low[u] = min(low[u], lab[v]);31
 }
}32
 }
}33
 void find(int u)
void find(int u)34


 {
{35
 visit[u] = true;
visit[u] = true;36
 list<int>::iterator it;
list<int>::iterator it;37
 for(it = g[u].begin(); it != g[u].end(); it++)
for(it = g[u].begin(); it != g[u].end(); it++)38
 if(!visit[*it])
if(!visit[*it])39
 find(*it);
find(*it);40
 }
}41
 int main()
int main()42


 {
{43
 t = 1;
t = 1;44
 while(1)
while(1)45


 {
{46
 scanf("%d", &v1);
scanf("%d", &v1);47
 if(v1 == 0) break;
if(v1 == 0) break;48
 for(int i=1; i<=1000; i++)
for(int i=1; i<=1000; i++)49
 g[i].clear();
g[i].clear();50
 memset(spf, 0, sizeof spf);
memset(spf, 0, sizeof spf);51
 memset(low, 0, sizeof low);
memset(low, 0, sizeof low);52
 memset(lab, 0, sizeof lab);
memset(lab, 0, sizeof lab);53
 while(v1 != 0)
while(v1 != 0)54


 {
{55
 scanf("%d", &v2);
scanf("%d", &v2);56
 g[v1].push_back(v2);
g[v1].push_back(v2);57
 g[v2].push_back(v1);
g[v2].push_back(v1);58
 root = v1;
root = v1;59
 scanf("%d", &v1);
scanf("%d", &v1);60
 }
}61
 counter = 1;
counter = 1;62
 flag = false;
flag = false;63
 dfs(root, -1);
dfs(root, -1);64
 printf("Network #%d\n", t++);
printf("Network #%d\n", t++);65
 if(flag)
if(flag)66


 {
{67
 for(int i=1; i<=1000; i++)
for(int i=1; i<=1000; i++)68


 {
{69
 if(!spf[i]) continue;
if(!spf[i]) continue;70
 int cnt = 0;
int cnt = 0;71
 memset(visit, 0, sizeof visit);
memset(visit, 0, sizeof visit);72
 visit[i] = true;
visit[i] = true;73
 list<int>::iterator it;
list<int>::iterator it;74
 for(it = g[i].begin(); it != g[i].end(); it++)
for(it = g[i].begin(); it != g[i].end(); it++)75
 if(!visit[*it])
if(!visit[*it])76


 {
{77
 cnt++;
cnt++;78
 find(*it);
find(*it);79
 }
}80
 printf(" SPF node %d leaves %d subnets\n", i, cnt);
printf(" SPF node %d leaves %d subnets\n", i, cnt);81
 }
}82
 }
}83
 else
else84
 printf(" No SPF nodes\n");
printf(" No SPF nodes\n");85
 printf("\n");
printf("\n");86
 }
}87
 }
}
For each test case,in the first line there are two numbers n(2<=n<=40000) and m (1<=m<=200),the number of houses and the number of queries. The following n-1 lines each consisting three numbers i,j,k, separated bu a single space, meaning that there is a road connecting house i and house j,with length k(0<k<=40000).The houses are labeled from 1 to n.
Next m lines each has distinct integers i and j, you areato answer the distance between house i and house j.
2 3 2 1 2 10 3 1 15 1 2 2 3 2 2 1 2 100 1 2 2 1
10 25 100 100
õ║īŃĆüÕłåµ×?br> ńö©TarjanĶ¦ŻÕå│ńÜäLCAķŚ«ķóśÕQīĶ»”Šlåń«Śµ│Ģ’╝Ü(x©¼)LCAķŚ«ķóśŃĆ?/span>
õĖēŃĆüõ╗ŻńĀ?/p>
 #include<iostream>
#include<iostream>
2 #include<list>
#include<list>
3 using namespace std;
using namespace std;
4 struct node
struct node
5

 {
{
6 int v, d;
int v, d;
7
 void init(int vv, int dd)
void init(int vv, int dd)  {v = vv; d = dd;};
{v = vv; d = dd;};
8 };
};
9 int t, n, m, v1, v2, len;
int t, n, m, v1, v2, len;
10 list<node> g[40001];
list<node> g[40001];
11 list<node> query[40001];
list<node> query[40001];
12 int dis[40001];
int dis[40001];
13 int res[201][3];
int res[201][3];
14 int parent[40001];
int parent[40001];
15 bool visit[40001];
bool visit[40001];
16 int find(int k)
int find(int k)
17

 {
{
18 if(parent[k] == k)
if(parent[k] == k)
19 return k;
return k;
20 return parent[k] = find(parent[k]);
return parent[k] = find(parent[k]);
21 }
}
22 void tarjan(int u)
void tarjan(int u)
23

 {
{
24 if(visit[u]) return;
if(visit[u]) return;
25 visit[u] = true;
visit[u] = true;
26 parent[u] = u;
parent[u] = u;
27 list<node>::iterator it = query[u].begin();
list<node>::iterator it = query[u].begin();
28 while(it != query[u].end())
while(it != query[u].end())
29

 {
{
30 if(visit[it->v])
if(visit[it->v])
31 res[it->d][2] = find(it->v);
res[it->d][2] = find(it->v);
32 it++;
it++;
33 }
}
34 it = g[u].begin();
it = g[u].begin();
35 while(it != g[u].end())
while(it != g[u].end())
36

 {
{
37 if(!visit[it->v])
if(!visit[it->v])
38

 {
{
39 dis[it->v] = min(dis[it->v], dis[u] + it->d);
dis[it->v] = min(dis[it->v], dis[u] + it->d);
40 tarjan(it->v);
tarjan(it->v);
41 parent[it->v] = u;
parent[it->v] = u;
42 }
}
43 it++;
it++;
44 }
}
45 }
}
46 int main()
int main()
47

 {
{
48 scanf("%d", &t);
scanf("%d", &t);
49 while(t--)
while(t--)
50

 {
{
51 scanf("%d%d", &n, &m);
scanf("%d%d", &n, &m);
52 for(int i=1; i<=n; i++)
for(int i=1; i<=n; i++)
53 g[i].clear();
g[i].clear();
54 for(int i=1; i<=m; i++)
for(int i=1; i<=m; i++)
55 query[i].clear();
query[i].clear();
56 for(int i=1; i<n; i++)
for(int i=1; i<n; i++)
57

 {
{
58 scanf("%d%d%d", &v1, &v2, &len);
scanf("%d%d%d", &v1, &v2, &len);
59 node n1; n1.init(v2, len);
node n1; n1.init(v2, len);
60 g[v1].push_back(n1);
g[v1].push_back(n1);
61 node n2; n2.init(v1, len);
node n2; n2.init(v1, len);
62 g[v2].push_back(n2);
g[v2].push_back(n2);
63 }
}
64 for(int i=1; i<=m; i++)
for(int i=1; i<=m; i++)
65

 {
{
66 scanf("%d%d", &v1, &v2);
scanf("%d%d", &v1, &v2);
67 res[i][0] = v1;
res[i][0] = v1;
68 res[i][1] = v2;
res[i][1] = v2;
69 node n1; n1.init(v2, i);
node n1; n1.init(v2, i);
70 query[v1].push_back(n1);
query[v1].push_back(n1);
71 node n2; n2.init(v1, i);
node n2; n2.init(v1, i);
72 query[v2].push_back(n2);
query[v2].push_back(n2);
73 }
}
74 memset(visit, 0, sizeof(visit));
memset(visit, 0, sizeof(visit));
75 memset(dis, 0x7f, sizeof(dis));
memset(dis, 0x7f, sizeof(dis));
76 dis[1] = 0;
dis[1] = 0;
77 tarjan(1);
tarjan(1);
78 for(int i=1; i<=m; i++)
for(int i=1; i<=m; i++)
79 printf("%d\n", dis[res[i][0]] + dis[res[i][1]] - 2*dis[res[i][2]]);
printf("%d\n", dis[res[i][0]] + dis[res[i][1]] - 2*dis[res[i][2]]);
80 }
}
81 }
}
µ£Ć׫ÅĶ┤╣ńö©µ£ĆÕż¦µĄüÕQÜĶ«ŠGµś»õ╗źsõĖ║µ║ÉtõĖ║µ▒ćńÜäńĮæŠl£’╝īcµś»GńÜäÕ«╣ķćÅ’╝ībµś»GńÜäÕŹĢõĮŹµĄüķćÅĶ┤╣ńö©’╝īõĖöµ£ēb[i][j] = -b[i][j]ÕQīfµś»GńÜ䵥üÕQīÕłÖb(f)=Ōł?fij*bij)ÕQ?i, j)∈E(G) õĖöfij>0ŃĆéµ£Ć׫ÅĶ┤╣ńö©µ£ĆÕż¦µĄüķŚ«ķóśÕQīÕ░▒µś»µ▒éŠ|æń╗£GńÜäµ£ĆÕż¦µĄüfõĖöõŗ╔Ķ┤╣ńö©b(f)µ£Ć׫ÅŃĆéĶ┐ÖµĀ’L(f©źng)Üäŗ╣üń¦░õĖ║µ£Ć׫ÅĶ┤╣ńö©µ£ĆÕż¦µĄüŃĆ?/span>
õ║īŃĆüń«Śµ│ĢµĆصā│
ńö©Ford-FulkersonĮÄŚµ│ĢńÜäµĆصā│ÕQīõĖŹµ¢ŁÕ£░Õ£©µ«ŗ(hu©ż)ńĢÖńĮæŠl£õĖŁÕ»└LēŠÕó×Õ╣┐ĶĘ»’╝īÕŬõĖŹśqćĶ┐ÖõĖ¬Õóדq┐ĶĄ\µś»ÕĮōÕēŹńĮæŠl£õĖŁsÕł░tńÜäõ╗źÕŹĢõĮŹŗ╣üķćÅĶ┤╣ńö©õĖ║µØāńÜäµ£Ćń¤ŁĶĄ\ÕQīÕ»╣śqÖµØĪÕó×Õ╣┐ĶĘ»Ķ┐øĶĪīµōŹõĮ£ŃĆéńö▒õ║ÄĶ┤╣ńö©µ£ēĶ┤¤ÕĆ¹|╝īÕ╗°Ö««ńö©SPFAĮÄŚµ│ĢŃĆ?br>õĖēŃĆüń«Śµ│Ģõ╗ŗŠl?br> µÅÅĶ┐░ÕQ?/span>
2 for each edge(u, v) in E(G)
3 do f[u, v] = 0
4 f[v, u] = 0
5 while exists a path p from s to t in Gf and p is the shortest path
6 do cf(p) = min{cf(u, v) : (u, v) in p}
7 for each edge(u, v) in p
8 do f[u, v] = f[u, v] + cf(p)
9 f[v, u] = - f[u, v]
 mcmf()
mcmf()2


 {
{3
 while(true)
while(true)4


 {
{5
 for(int i=1; i<=n+m+1; i++)
for(int i=1; i<=n+m+1; i++)6
 d[i] = MAX;
d[i] = MAX;7
 d[s] = 0;
d[s] = 0;8
 spfa(); //põĖŁÕŁśµ£ēĶ»źńé╣ńÜäÕēŹńæ¶(h©┤)ńé?/span>
spfa(); //põĖŁÕŁśµ£ēĶ»źńé╣ńÜäÕēŹńæ¶(h©┤)ńé?/span>9
 if(p[t] == -1) //ĶĪ©ńż║ÕĘ▓µŚĀÕó×Õ╣┐ĶĘ?/span>
if(p[t] == -1) //ĶĪ©ńż║ÕĘ▓µŚĀÕó×Õ╣┐ĶĘ?/span>10
 break;
break;11
 int minf = INT_MAX;
int minf = INT_MAX;12
 int it = t;
int it = t;13
 while(p[it] != -1)
while(p[it] != -1)14


 {
{15
 minf = min(minf, c[p[it]][it] - f[p[it]][it]);
minf = min(minf, c[p[it]][it] - f[p[it]][it]);16
 it = p[it];
it = p[it];17
 }
}18
 it = t;
it = t;19
 while(p[it] != -1)
while(p[it] != -1)20


 {
{21
 f[p[it]][it] += minf;
f[p[it]][it] += minf;22
 f[it][p[it]] = -f[p[it]][it];
f[it][p[it]] = -f[p[it]][it];23
 it = p[it];
it = p[it];24
 }
}25
 }
}26
 }
}õĖēŃĆüń«Śµ│Ģńż║õŠ?br> POJ 2516 Ķ¦ŻķóśµŖźÕæŖ
ÕīÜwģŹÕQÜĶ«ŠG(V, E)õĖ║µŚĀńÄ»ÕøŠÕQīĶ«ŠMõĖ║EńÜäõĖĆõĖ¬ķØ×ĮI║ÕŁÉķøå’╝īÕ”éµ×£MõĖŁńÜäõ╗└LäÅõĖżµØĪĶŠ╣Õ£©GõĖŁõĖŹńøöRé╗ÕQīÕłÖ┐U░Mµś»ÕøŠGõĖŁńÜäõĖĆõĖ¬Õī╣ķģŹŃĆéĶŗźÕ»╣ÕøŠGńÜäõōQõĮĢÕī╣ķģŹM'ÕQīÕØćµ£ē|M'|≤|M|ÕQīÕłÖ┐U░MõĖ║GńÜäµ£ĆÕż¦Õī╣ķģŹŃĆ?br> ķź▒ÕÆīńé╣’╝Ü(x©¼)Ķ«ŠMµś»ÕøŠGõĖŁńÜäÕīÜwģŹÕQīGõĖŁõĖÄMõĖŁńÜäĶŠ╣Õģ│ĶüöńÜäÖÕČńé╣┐UŅCžō(f©┤)Mķź▒ÕÆīńé╣’╝īÕÉ”ÕłÖ┐UŅCžō(f©┤)MķØ×ķź▒ÕÆīńé╣ŃĆéĶŗźÕøŠõĖŁÖÕČńé╣ÕØ浜»Mķź▒ÕÆīńé╣’╝īÕłÖń¦░MõĖ║GńÜäÕ«īŠ¤ÄÕī╣ķģŹŃĆ?br> Mõ║żķöÖĶĘ»’╝Ü(x©¼)Ķ«ŠPµś»GńÜäõĖƵØĪĶĄ\ÕQīõĖöÕ£©PõĖŁ’╝īMńÜäĶŠ╣ÕÆīE-MńÜäĶŠ╣õ║żķöÖÕć║ńÄ░ÕQīÕłÖ┐U░Pµś»GńÜäõĖƵØĪMõ║żķöÖĶĘ»ŃĆéĶŗźMõ║żķöÖĶĘ»PńÜäõĖżõĖ¬ń½»ńé╣õžō(f©┤)MķØ×ķź▒ÕÆīńé╣ÕQīÕłÖ┐U░PõĖ║MÕÅ»Õóדq┐ĶĄ\ŃĆ?nbsp;
µĀ╣Õ£©xńÜäMõ║żķöÖÕŁÉÕøŠÕQÜĶ«ŠxõĖ║GõĖŁMķØ×ķź▒ÕÆīńé╣ŃĆéGõĖŁńö▒ĶĄ’L(f©źng)é╣õĖ║xńÜäMõ║żķöÖĶĘ»µēĆĶāĮĶ┐׵ğńÜäÖÕČńé╣ķøåµēĆÕ»╝Õć║ńÜäGńÜäÕ»╝Õć║ÕŁÉÕøŠŃĆ?br> SńÜäķé╗ķøå’╝Ü(x©¼)Ķ«ŠSõĖ║GńÜäõōQõĖĆÖÕČńé╣ķøå’╝īGõĖŁõĖÄSńÜäķĪČńéÜwé╗µÄźńÜäµēƵ£ēķĪČńé╣ńÜäķøåÕÉłÕQīń¦░õĖ║SńÜäķé╗ķøå’╝īĶ«ŅCĮ£N(S)ŃĆ?br> µ£Ćõ╝śÕī╣ķģŹ’╝Ü(x©¼)Õ»╣õ║ÄõĖĆõĖ¬ÕŖĀµØāõ║īķā©ÕøŠÕQīõĖĆõĖ¬µØāµ£ĆÕż¦ńÜäÕīÜwģŹÕŽõĮ£µ£Ćõ╝śÕī╣ķģŹŃĆ?br> ÕÅ»ĶĪīիܵĀćÕQܵśĀ׫älÕQÜV(G)→RÕQīµ╗ĪŁæø_»╣GńÜ䵻ŵØĪĶŠ╣e={u, v}ÕQīÕØćµ£ēl(u)+l(v)≥w(u, v)ÕQīÕģČõĖŁw(u, v)ĶĪ©ńż║ĶŠ╣eńÜäµØāÕQīÕłÖ┐U░l(f©Ī)õĖ║GńÜäÕÅ»ĶĪīķĪȵĀćŃĆéõūo(h©┤)El={(u, v) | {u, v}∈E(G)ÕQīl(u)+l(v)=w(u, v)}ÕQīGlõĖ▐Z╗źElõĖ°ÖŠ╣ķøåńÜäGńÜäńö¤µłÉÕŁÉÕøŠ’╝īÕłÖń¦░GlõĖ║lĮ{ēÕŁÉÕøŠŃĆ?br>õ║īŃĆüµ£ĆÕż¦Õī╣ķģŹ’╝łÕīłńēÖÕł®ń«Śµ│Ģ’╝ē(j©¬)
µÅÅĶ┐░ÕQ?/strong>
ÕQ?ÕQēGµś»Õģʵ£ēÕłÆÕł?V1, V2)ńÜäõ║īÕłåÕøŠÕQīõōQŠlÖÕłØÕ¦ŗÕī╣ķģŹMÕQ?br> ÕQ?ÕQēĶŗźMķź▒ÕÆīV1ÕłÖń╗ōµØ¤’╝ø
ÕQ?ÕQēÕÉ”ÕłÖ’╝īÕ£©V1õĖŁµēŠõĖĆMķØ×ķź▒ÕÆīńé╣ÕQī’╝īŠ|«S={x}ÕQ?TõĖ║ń®║ÕQ?br> ÕQ?ÕQēĶŗźN(S) = TÕQīÕłÖÕü£µŁóÕQīÕÉ”ÕłÖõōQķĆēõĖĆńé╣y∈N(S)-TÕQ?br> ÕQ?ÕQēĶŗźyõĖ║MķØ×ķź▒ÕÆīńé╣ÕQīÕłÖµ▒éõĖƵØĪõ╗ÄxÕł░yńÜäMÕÅ»Õóדq┐ĶĄ\PÕQīńĮ«MõĖ║MÕ╝鵳¢P“qČĶØ{ÕQ?ÕQē’╝ø
ÕQ?ÕQēÕÉ”ÕłÖ’╝īńöūā║Äyµś»MńÜäķź▒ÕÆīńé╣ÕQīµĢģMõĖŁµ£ēõĖĆĶŠ╣{y, u}ÕQīńĮ«S = S∪{u}ÕQīT = T∪{y}ÕQīĶØ{ÕQ?ÕQēŃĆ?br> Õ«×ńÄ░ÕQ?br>
2 for i : 1 to |V2|
3 do match[i] = 0
4 for each vertex u in V1
5 do for i : 1 to |V2|
6 do visit[i] = false
7 DFS(u)
8 DFS(u)
9 for each vertex v in V2
10 if (u, v) in E(G) and visit[v] is false
11 then visit[v]=true
12 if match[v] is 0 or DFS(match[v]) is true
13 then match[v] = u
14 return true
15 return false
Ķ»┤µśÄÕQ?/strong>ĮW?ĶĪīńÜäDFS(u)śqćń©ŗÕQīÕĮōÕŁśÕ£©õ╗ÄuÕ╝ĆÕ¦ŗńÜäMÕÅ»Õóדq┐ĶĄ\ÕQīÕłÖśqöÕø×trueÕQīÕŲłÕ«īµłÉMńÜäµē®Õ▒Ģ’╝īµŁżµŚČ|M|ÕŖĀõĖĆŃĆéÕ”éµ×£Ķ┐öÕø×falseÕQīÕłÖĶĪ©ńż║õĖŹÕŁśÕ£©MÕÅ»Õóדq┐ĶĄ\ŃĆ?nbsp;
ĮC▐ZŠŗÕQ?/strong>POJ 1274 Ķ¦ŻķóśµŖźÕæŖŃĆ?/span>
õĖēŃĆüµ£Ćõ╝śÕī╣ķģŹ’╝łKMĮÄŚµ│ĢÕQ?br> µÅÅĶ┐░ÕQ?/strong>
ÕQ?ÕQēõ╗Äõ╗└LäÅÕÅ»ĶĪīÖÕȵĀćlÕ╝ĆÕ¦ŗ’╝ī╝ŗ«Õ«ÜlĮ{ēÕŁÉÕøŠGlÕQīÕŲłõĖöÕ£©GlõĖŁķĆēÕÅ¢ÕīÜwģŹMŃĆéĶŗźMķź▒ÕÆīV1ÕQīÕłÖMµś»Õ«īŠ¤ÄÕī╣ķģŹ’╝īõ╣¤ÕŹ│Mµś»µ£Ćõ╝śÕī╣ķģŹ’╝īĮÄŚµ│ĢŠlłµŁóÕQ?br> ÕQ?ÕQēÕÉ”ÕłÖ’╝īśqÉńö©ÕīłńēÖÕł®ń«Śµ│Ģ’╝īŠlłµŁóõ║ÄSÕ▒×õ║ÄV1ÕQīTÕ▒×õ║ÄV2õĖöõŗ╔Õ»╣õ║ÄGlÕQīN(S)=TŃĆéõūo(h©┤)al=min{l(x)+l(y)-w(x, y) | x∈S, y∈V2-T}ÕQīõūo(h©┤)l'(u)=l(u)-alÕ”éµ×£u∈SÕQøl'(u)=l(u)+alÕ”éµ×£u∈TÕQøl'(u)=l(u)ÕQīÕģČÕ«āŃĆéńö©l'õ╗Żµø┐lÕQīńö©Gl'õ╗Żµø┐GlĶĮ¼ÕģźÕQ?ÕQēŃĆ?br> Õ«×ńÄ░ÕQ?/strong>
2 for each vertex u in V1
3 do lx[u] = max{w[u][v] | (u, v) in E(G)}
4 for each vertex v in V2
5 do ly[v] = 0
6 for each vertex u in V1
7 do while(true)
8 do for each vertex u in V1
9 do vx[u] = false
10 for each vertex v in V2
11 do vy[v] = false
12 slack[v] = MAX
13 if DFS(u) is true
14 then break
15 d = min{slack[v] | v in V2 and vy[v] is false}
16 for each vertex u in V1
17 do lx[u] = lx[u] - d
18 for each vertex v in V2
19 do ly[v] = ly[v] + d
20 DFS(u)
21 vx[u] = true
22 for each vertex v in V2
23 do if lx[u]+ly[v]==w[u][v] and vy[v] is false
24 then vy[v] = true
25 if match[v] is NIL or DFS(match[v])
26 then match[v] = u
27 return true
28 else if lx[u]+ly[v]>w[u][v]
29 then slack[v] = min{slack[v], lx[u]+ly[v]-w[u][v]}
30 return false