斐波那契(Fabonacci)序列起源于中世紀(jì)的意大利���,問題是這樣給出的:假定每對兔子每個(gè)月生出新的一對兔子來�����,新的每對兔子過兩個(gè)月就可以生育�����。其次���,這些兔子都不死�����,這樣第一個(gè)月有一對兔子,第二個(gè)月有兩對兔子���,第三個(gè)月有三對兔子(第一個(gè)月的一對兔子又生了一對),第四個(gè)月有五對兔子(第二個(gè)月已有的兩對兔子又各生了一對)�����,以此類推�����,問一年共有多少對兔子。
可以把這個(gè)問題抽象一下:一般每個(gè)月的兔子數(shù)為上個(gè)月已有的兔子(因?yàn)橥米硬凰溃┖?strong>上上個(gè)月已有兔子新生的兔子(兔子兩個(gè)月后就可以生育)之和,也就是說�����,序列中的某一項(xiàng)等于前兩項(xiàng)之和(雖然一開始不成立)���。
于是乎得到了所謂的斐波那契序列�,它定義為:
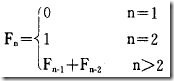
就是說:從第三項(xiàng)起每項(xiàng)都是前兩項(xiàng)的和。
在下面的算法里���,把第一項(xiàng)看作了 0,這樣就更符合數(shù)學(xué)上的“斐波那契”數(shù)列了:
1���,使用遞歸方法:
return (Fabonacci(n - 1) + Fabonacci(n - 2)); |
2,使用 for 循環(huán)�,輸出了前 n 個(gè)斐波那契數(shù)列:
int _Fabonacci(int n)//輸出前 n 個(gè)數(shù) |
printf("%10d%10d", a, b);/*輸出前兩個(gè)數(shù)*/ |
printf("\n");/*每行輸出 5 個(gè)*/ |
b = c;/*項(xiàng)移動(dòng)*/ |
}