22.4-1:
不得不說老外有時候也挺變態的,搞這么復雜個圖...考概念你把圖弄小點啊,考這么大,嚇死我這種剛入門的小菜鳥小朋友咋辦
寫紙上了略了,耐心點就好
22.4-2:
開始覺得是深搜,試了一下不行
然后聯想到這節講的就是拓排...肯定得用拓排啦(填鴨式教育的思維啊...)
不過還是沒想出來線性算法,到處搜答案...汗,一搜搜到斯坦福的一篇作業講解,牛叉學校果然不一樣
看的結果是——動態規劃...
看來DP快點上手了
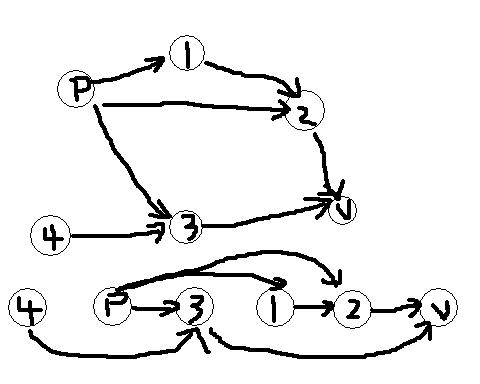
演示圖(標記為數字的完全是為方便DFS時候的順序,假設同22.3-2)
(1)拓排,即可得類似P336,圖22-7所示的從左到右的一個順序關系,即上圖下部分的樣子
(2)DP一下
記P[v]為s到v的路徑數,初始化為0
把P[p]設為1
P[v]=∑(u,v)belongs to EP[u]
也就是說等于所有拓撲序前面的與之相邊的頂點的P[]之和
復雜度為:
拓排: O(V+E)
左到右掃一遍DP:V
所以為O(V+E)
不明白的地方:用啥數據結構表示呢?
A:鄰接表...
http://www-cs-students.stanford.edu/phd/comps/2007/2007-Analysis_of_Algorithms-solutions.pdf
22.4-3: