定理：n個(gè)1 和n個(gè)-1 構(gòu)成的2n項(xiàng) a1,a2….a2n ,其部分和

滿(mǎn)足 a1 + a2 + …aK >= 0 (k = 1 2 … 2n ) 這個(gè)的條件的個(gè)數(shù) 為

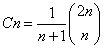
證明：令A(yù)n 為其中可以接受的系列Bn 為不可接受的系列

那么 An + Bn = .An 是我們要求的，我們可以通過(guò)求出Bn來(lái)得到An 。

我們假設(shè)存在 一個(gè)最小的K 使得a1 + a2 +…+ak 為負(fù)，那么 可以肯定 a1+…+ak-1 = 0,且ak = -1.k 為奇整數(shù)。

對(duì)于每一種不符合條件的序列a1 + a2 +…+ak +…+a2n 將a1 a2 ak 都用-a1 –a2 –ak 代替，那么新的數(shù)列

a1’ a2’ … a2n’ 就有 n+1 個(gè) +1 和 n-1 個(gè) –1  。即每一種 不符合條件的 數(shù)列經(jīng)過(guò)上述過(guò)程都將變?yōu)?/p>

  n+1 個(gè) +1 和 n-1 個(gè) –1   的排列 。那么現(xiàn)在要證明 n+1 個(gè) +1 和 n-1 個(gè) –1   的排列數(shù) == Bn

n+1 個(gè) +1 和 n-1 個(gè) –1   的排列 肯定存在一個(gè) 最小的k 使得 a1 + a2 + …aK <  0   而將這部分也用-a1 –a2 –ak 代替 ，也就成為了 n個(gè)1 和n個(gè)-1 構(gòu)成的2n項(xiàng) a1,a2….a2n   而B(niǎo)n的排列就好求了

==》 

應(yīng)用： 有2n個(gè)人要去劇場(chǎng)，入場(chǎng)5角，有n個(gè)人有1元，n個(gè)人有5角，劇場(chǎng)的賣(mài)票處剛開(kāi)始沒(méi)有零錢(qián)，那么存在多少種隊(duì)列方式。

粗體的證明 ，我感覺(jué)有些牽強(qiáng)，呵呵 大家有好的方法，請(qǐng)指正。

我獨(dú)立博客地址 http://www.fuxiang90.me/?p=286