| Time Limit: 3000MS | Memory Limit: 65536K | |
| Total Submissions: 4189 | Accepted: 1501 |
Description
Stan has n sticks of various length. He throws them one at a time on the floor in a random way. After finishing throwing, Stan tries to find the top sticks, that is these sticks such that there is no stick on top of them. Stan has noticed that the last thrown stick is always on top but he wants to know all the sticks that are on top. Stan sticks are very, very thin such that their thickness can be neglected.
Input
Input consists of a number of cases. The data for each case start with 1 <= n <= 100000, the number of sticks for this case. The following n lines contain four numbers each, these numbers are the planar coordinates of the endpoints of one stick. The sticks are listed in the order in which Stan has thrown them. You may assume that there are no more than 1000 top sticks. The input is ended by the case with n=0. This case should not be processed.
Output
For each input case, print one line of output listing the top sticks in the format given in the sample. The top sticks should be listed in order in which they were thrown.
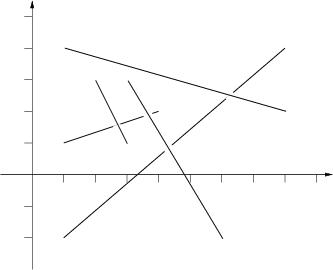
The picture to the right below illustrates the first case from input.
The picture to the right below illustrates the first case from input.
Sample Input
5 1 1 4 2 2 3 3 1 1 -2.0 8 4 1 4 8 2 3 3 6 -2.0 3 0 0 1 1 1 0 2 1 2 0 3 1 0
Sample Output
Top sticks: 2, 4, 5. Top sticks: 1, 2, 3.
Hint
Huge input,scanf is recommended.
/***********************************
鏆村姏灝辮錛屼粠絎竴涓紑濮嬪垽鏂?br />濡傛灉涓ゆ潯綰挎鐩鎬氦灝辨妸鍓嶉潰涓鏉＄瓫閫夋帀鍒ゆ柇綰挎鐩鎬氦鐩存帴璐寸殑鍚夊ぇ妯℃澘銆傘傘?br />
***********************************/
#include <iostream>#include <cstdio>#include <cstring>using namespace std;const int maxn = 100000 + 5;const double eps=1e-10;struct point { double x, y; };
point p[maxn], b[maxn];bool ans[maxn];double min(double a, double b) { return a < b ? a : b; }double max(double a, double b) { return a > b ? a : b; }bool inter(point a, point b, point c, point d){ if( min(a.x, b.x) > max(c.x, d.x) || min(a.y, b.y) > max(c.y, d.y) || min(c.x, d.x) > max(a.x, b.x) || min(c.y, d.y) > max(a.y, b.y) ) return 0; double h, i, j, k; h = (b.x - a.x) * (c.y - a.y) - (b.y - a.y) * (c.x - a.x); i = (b.x - a.x) * (d.y - a.y) - (b.y - a.y) * (d.x - a.x); j = (d.x - c.x) * (a.y - c.y) - (d.y - c.y) * (a.x - c.x); k = (d.x - c.x) * (b.y - c.y) - (d.y - c.y) * (b.x - c.x); return h * i <= eps && j * k <= eps;}int main(){ int n; int res[maxn]; while( cin >> n, n )
{
memset( ans, 0, sizeof( ans ) ); for( int i = 0; i < n; i++ ) { cin >> p[i].x >> p[i].y >> b[i].x >> b[i].y;
} for( int i = 0; i < n; i++ ) { for( int j = i + 1; j < n; j++ ) { if( inter(p[i], b[i], p[j], b[j] ) ) { ans[i] = 1; break; //涓嶅姞break浼氳秴鏃躲傘傘?/span> } } } int ct = 0; cout << "Top sticks: "; for( int i = 0; i < n; i++ ) if( !ans[i] ) res[ct++] = i + 1; for( int i = 0; i < ct - 1; i++ ) cout << res[i] << ", "; cout << res[ct-1] << "." << endl; } return 0;}]]>
Intersecting Lines
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 4260 | Accepted: 2049 |
Description
We all know that a pair of distinct points on a plane defines a line and that a pair of lines on a plane will intersect in one of three ways: 1) no intersection because they are parallel, 2) intersect in a line because they are on top of one another (i.e. they are the same line), 3) intersect in a point. In this problem you will use your algebraic knowledge to create a program that determines how and where two lines intersect.
Your program will repeatedly read in four points that define two lines in the x-y plane and determine how and where the lines intersect. All numbers required by this problem will be reasonable, say between -1000 and 1000.
Your program will repeatedly read in four points that define two lines in the x-y plane and determine how and where the lines intersect. All numbers required by this problem will be reasonable, say between -1000 and 1000.
Input
The first line contains an integer N between 1 and 10 describing how many pairs of lines are represented. The next N lines will each contain eight integers. These integers represent the coordinates of four points on the plane in the order x1y1x2y2x3y3x4y4. Thus each of these input lines represents two lines on the plane: the line through (x1,y1) and (x2,y2) and the line through (x3,y3) and (x4,y4). The point (x1,y1) is always distinct from (x2,y2). Likewise with (x3,y3) and (x4,y4).
Output
There should be N+2 lines of output. The first line of output should read INTERSECTING LINES OUTPUT. There will then be one line of output for each pair of planar lines represented by a line of input, describing how the lines intersect: none, line, or point. If the intersection is a point then your program should output the x and y coordinates of the point, correct to two decimal places. The final line of output should read "END OF OUTPUT".
Sample Input
5 0 0 4 4 0 4 4 0 5 0 7 6 1 0 2 3 5 0 7 6 3 -6 4 -3 2 0 2 27 1 5 18 5 0 3 4 0 1 2 2 5
Sample Output
INTERSECTING LINES OUTPUT POINT 2.00 2.00 NONE LINE POINT 2.00 5.00 POINT 1.07 2.20 END OF OUTPUT
]]>