---------------
什么是 Hash
Hash 的重要特�?nbsp;
Hash 函数的实�?nbsp;
主要�?Hash ���法
Hash ���法的安全问�?nbsp;
Hash ���法的应�?nbsp;
�l?�?nbsp;
---------------
Hash�Q�一般翻译做“散列”�Q�也有直接音译�ؓ"哈希"的,���是把�Q意长度的输入�Q�又叫做预映���, pre-image�Q�,通过散列���法�Q�变换成固定长度的输出,该输出就是散列倹{��这�U��{换是一�U�压�~�映���,也就是,散列值的�I�间通常�q�小于输入的�I�间�Q�不同的输入可能会散列成相同的输出,而不可能从散列值来唯一的确定输入倹{�?/p>
数学表述为:h = H(M) �Q�其中H( )--单向散列函数�Q�M--��L��长度明文�Q�h--固定长度散列倹{�?/p>
在信息安全领域中应用的Hash���法�Q�还需要满���_��他关键特性:
�W�一当然是单向�?one-way)�Q�从预映���,能够���单迅速的得到散列��|��而在计算上不可能构造一个预映射�Q���其散列结果等于某个特定的散列��|����x��造相应的M=H-1(h)不可行。这��P��散列值就能在�l�计上唯一的表征输入��|��因此�Q�密码学上的 Hash 又被�U�Cؓ"消息摘要(message digest)"�Q�就是要求能方便的将"消息"�q�行"摘要"�Q�但�?摘要"中无法得到比"摘要"本��n更多的关�?消息"的信息�?/p>
�W�二是抗冲突�?collision-resistant)�Q�即在统计上无法产生2个散列值相同的预映���。给定M�Q�计���上无法扑ֈ�M'�Q�满���H(M)=H(M') �Q�此谓弱抗冲�H�性;计算上也难以��L��一对�Q意的M和M'�Q���满��H(M)=H(M') �Q�此谓强抗冲�H�性。要�?强抗冲突�?主要是�ؓ了防范所�?生日��d��(birthday attack)"�Q�在一�?0人的团体中,你能扑ֈ�和你生日相同的�h的概率是2.4%�Q�而在同一团体中,�?人生日相同的概率�?1.7%。类似的�Q�当预映���的�I�间很大的情况下�Q�算法必���L�����_��的强度来保证不能��L��扑ֈ�"相同生日"的�h�?/p>
�W�三是映���分布均匀性和差分分布均匀性,散列�l�果中,�?0 �?bit 和�ؓ 1 �?bit �Q�其��L��应该大致相等�Q�输入中一�?bit 的变化,散列�l�果中将有一半以上的 bit 改变�Q�这又叫�?雪崩效应(avalanche effect)"�Q�要实现使散列结果中出现 1bit 的变化,则输入中臛_��有一半以上的 bit 必须发生变化。其实质是必���M��输入中每一�?bit 的信息,���量均匀的反映到输出的每一�?bit 上去�Q�输��Z��的每一�?bit�Q�都是输入中���可能多 bit 的信息一起作用的�l�果�?/p>
Damgard �?Merkle 定义了所�?#8220;压羃函数(compression function)”�Q�就是将一个固定长度输入,变换成较短的固定长度的输出,�q�对密码学实践上 Hash 函数的设计��生了很大的媄响。Hash函数���是被设计�ؓ��Z��通过特定压羃函数的不断重�?#8220;压羃”输入的分�l�和前一�ơ压�~�处理的�l�果的过�E�,直到整个消息都被压羃完毕�Q�最后的输出作�ؓ整个消息的散列倹{��尽���还�~�Z��严格的证明,但绝大多��C��界的研究者都同意�Q�如果压�~�函数是安全的,那么以上�q��Ş式散列�Q意长度的消息也将是安全的。这���是所�?Damgard/Merkle �l�构�Q?/p>
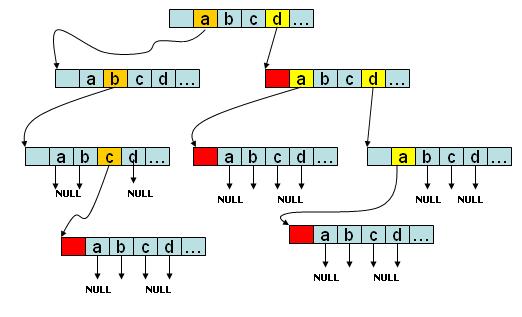
在下图中�Q��Q意长度的消息被分拆成�W�合压羃函数输入要求的分�l�,最后一个分�l�可能需要在末尾��M��特定的填充字节,�q�些分组���被��序处理�Q�除了第一个消息分�l�将与散列初始化��g��起作为压�~�函数的输入外,当前分组���和前一个分�l�的压羃函数输出一赯���作�ؓ�q�一�ơ压�~�的输入�Q�而其输出又将被作��Z��一个分�l�压�~�函数输入的一部分�Q�直到最后一个压�~�函数的输出�Q�将被作为整个消息散列的�l�果�?/p>
MD5 �?SHA1 可以说是目前应用最�q�泛的Hash���法�Q�而它们都是以 MD4 为基���设计的�?/p>
1) MD4
MD4(RFC 1320)�?MIT �?Ronald L. Rivest �?1990 �q�设计的�Q�MD �?Message Digest 的羃写。它适用�?2位字长的处理器上用高速��Y件实�?-它是��Z�� 32 位操作数的位操作来实现的。它的安全性不像RSA那样��Z��数学假设�Q�尽��?Den Boer、Bosselaers �?Dobbertin 很快���q��分析和差分成功的��d��了它3轮变换中�?2 轮,证明了它�q�不像期望的那样安全�Q�但它的整个���法�q�没有真正被破解�q�,Rivest 也很快进行了改进�?/p>
下面是一些MD4散列�l�果的例子:
MD4 ("") = 31d6cfe0d16ae931b73c59d7e0c089c0
MD4 ("a") = bde52cb31de33e46245e05fbdbd6fb24
MD4 ("abc") = a448017aaf21d8525fc10ae87aa6729d
MD4 ("message digest") = d9130a8164549fe818874806e1c7014b
MD4 ("abcdefghijklmnopqrstuvwxyz") = d79e1c308aa5bbcdeea8ed63df412da9
MD4 ("ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789") = 043f8582f241db351ce627e153e7f0e4
MD4 ("12345678901234567890123456789012345678901234567890123456789012345678901234567890") = e33b4ddc9c38f2199c3e7b164fcc0536
2) MD5
MD5(RFC 1321)�?Rivest �?991�q�对MD4的改�q�版本。它对输入仍�?12位分�l�,其输出是4�?2位字的��联,�?MD4 相同。它较MD4所做的改进是:
1) 加入了第四轮
2) 每一步都有唯一的加法常敎ͼ�
3) �W�二轮中的G函数�?(X �?Y) �?(X �?Z) �?(Y �?Z)) 变�ؓ ((X �?Z) �?(Y �?~Z))以减���其对称性;
4) 每一步都加入了前一步的�l�果�Q�以加快"雪崩效应"�Q?nbsp;
5) 改变了第2轮和�W?轮中讉K��输入子分�l�的��序�Q�减���了形式的相似程度;
6) �q�似优化了每轮的循环左移位移量,以期加快"雪崩效应"�Q�各轮的循环左移都不同�?nbsp;
���管MD5比MD4来得复杂�Q��ƈ且速度较之要慢一点,但更安全�Q�在抗分析和抗差分方面表现更好�?/p>
消息首先被拆成若�q�个512位的分组�Q�其中最�?12位一个分�l�是“消息��?填充字节(100…0)+64 位消息长�?#8221;�Q�以���保对于不同长度的消息,该分�l�不相同�?4位消息长度的限制��D��了MD5安全的输入长度必���d���?64bit�Q�因为大�?4位的长度信息���被忽略。�?�?2位寄存器字初始化为A=0x01234567�Q�B=0x89abcdef�Q�C=0xfedcba98�Q�D=0x76543210�Q�它们将始终参与�q�算�q��Ş成最�l�的散列�l�果�?/p>
接着各个512位消息分�l�以16�?2位字的�Ş式进入算法的��d�@环,512位消息分�l�的个数据决定了循环的次数。主循环�?轮,每轮分别用到了非�U�性函�?/p>
F(X, Y, Z) = (X �?Y) �?(~X �?Z)
G(X, Y, Z) = (X �?Z) �?(Y �?~Z)
H(X, Y, Z) =X ⊕ Y ⊕ Z
I(X, Y, Z) = X ⊕ (Y �?~Z)
�q?轮变换是对进入主循环�?12位消息分�l�的16�?2位字分别�q�行如下操作�Q�将A、B、C、D的副本a、b、c、d中的3个经F、G、H、I�q�算后的�l�果与第4个相加,再加�?2位字和一�?2位字的加法常敎ͼ��q�将所得之值��@环左�U�若�q�位�Q�最后将所得结果加上a、b、c、d之一�Q��ƈ回送至ABCD�Q�由此完成一�ơ��@环�?/p>
所用的加法常数��p��样一张表T[i]来定义,其中i�?…64�Q�T[i]是i的正弦绝对��g��4294967296�ơ方的整数部分,�q�样做是��Z��通过正��u函数和幂函数来进一步消除变换中的线性性�?/p>
当所�?12位分�l�都�q�算完毕后,ABCD的��联将被输��ZؓMD5散列的结果。下面是一些MD5散列�l�果的例子:
MD5 ("") = d41d8cd98f00b204e9800998ecf8427e
MD5 ("a") = 0cc175b9c0f1b6a831c399e269772661
MD5 ("abc") = 900150983cd24fb0d6963f7d28e17f72
MD5 ("message digest") = f96b697d7cb7938d525a2f31aaf161d0
MD5 ("abcdefghijklmnopqrstuvwxyz") = c3fcd3d76192e4007dfb496cca67e13b
MD5 ("ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789") = d174ab98d277d9f5a5611c2c9f419d9f
MD5 ("12345678901234567890123456789012345678901234567890123456789012345678901234567890") = 57edf4a22be3c955ac49da2e2107b67a
参考相应RFC文档可以得到MD4、MD5���法的详�l�描�q�和���法的C源代码�?/p>
3) SHA1 及其�?nbsp;
SHA1是由NIST NSA设计为同DSA一起��用的�Q�访问http://www.itl.nist.gov/fipspubs可以得到它的详细规范--[/url]"FIPS PUB 180-1 SECURE HASH STANDARD"。它寚w��度小�?64的输入,产生长度�?60bit的散列��|��因此抗穷�?brute-force)性更好。SHA-1 设计时基于和MD4相同原理,�q�且模仿了该���法。因为它������?60bit的散列��|��因此它有5个参与运���的32位寄存器字,消息分组和填充方式与MD5相同�Q�主循环也同��h��4轮,但每轮进�?0�ơ操作,非线性运���、移位和加法�q�算也与MD5�c�M���Q�但非线性函数、加法常数和循环左移操作的设计有一些区别,可以参考上面提到的规范来了解这些细节。下面是一些SHA1散列�l�果的例子:
SHA1 ("abc") = a9993e36 4706816a ba3e2571 7850c26c 9cd0d89d
SHA1 ("abcdbcdecdefdefgefghfghighijhijkijkljklmklmnlmnomnopnopq") = 84983e44 1c3bd26e baae4aa1 f95129e5 e54670f1
其他一些知名的Hash���法�q�有MD2、N-Hash、RIPE-MD、HAVAL�{�等。上面提到的�q�些都属�?�U?Hash���法。还有另2�c�Hash���法�Q�一�c�d��是基于对�U�分�l�算法的单向散列���法�Q�典型的例子是基于DES的所谓Davies-Meyer���法�Q�另外还有经IDEA改进的Davies-Meyer���法�Q�它们两者目前都被认为是安全的算法。另一�c�L����Z��模运��?���L���Ҏ��的,也就是基于公开密钥���法的,但因为其�q�算开销太大�Q�而缺乏很好的应用前景�?/p>
没有通过分析和差分攻击考验的算法,大多都已�l�夭折在实验室里了,因此�Q�如果目前流行的Hash���法能完全符合密码学意义上的单向性和抗冲�H�性,��׃��证了只有�I��D�Q�才是破坏Hash�q�算安全�Ҏ��的唯一�Ҏ��。�ؓ了对抗弱抗冲�H�性,我们可能要穷举个数和散列值空间长度一样大的输入,卛_���?^128�?^160个不同的输入�Q�目前一台高档个人电脑可能需�?0^25�q�才能完成这一艰巨的工作,即��是最高端的�ƈ行系�l�,�q�也不是在几千年里的�q�得完的事。而因�?生日��d��"有效的降低了需要穷丄����I�间�Q�将光���低�ؓ大约1.2*2^64�?.2*2^80�Q�所以,强抗冲突性是军_��Hash���法安全性的关键�?/p>
在NIST新的 Advanced Encryption Standard (AES)中,使用了长度�ؓ128�?92�?56bit 的密钥,因此相应的设计了 SHA256、SHA384、SHA512�Q�它们将提供更好的安全性�?/p>
Hash���法在信息安全方面的应用主要体现在以下的3个方面:
1) 文�g校验
我们比较熟悉的校验算法有奇偶校验和CRC校验�Q�这2�U�校验�ƈ没有抗数据篡改的能力�Q�它们一定程度上能检����ƈ�U�正数据传输中的信道误码�Q�但却不能防止对数据的恶意破坏�?/p>
MD5 Hash���法�?数字指纹"�Ҏ��,使它成�ؓ目前应用最�q�泛的一�U�文件完整性校验和(Checksum)���法�Q�不���Unix�pȝ��有提供计���md5 checksum的命令。它常被用在下面�?�U�情况下�Q?/p>
�W�一是文件传送后的校验,���得到的目标文�g计算 md5 checksum�Q�与源文件的md5 checksum 比对�Q�由两�?md5 checksum 的一致性,可以从统计上保证2个文件的每一个码元也是完全相同的。这可以���验文件传输过�E�中是否出现错误�Q�更重要的是可以保证文�g在传输过�E�中未被恶意���改。一个很典型的应用是ftp服务�Q�用户可以用来保证多�ơ断点箋传,特别是从镜像站点下蝲的文件的正确性�?/p>
更出色的解决�Ҏ��是所谓的代码�{���Q�文件的提供者在提供文�g的同�Ӟ��提供�Ҏ��件Hash值用自己的代码签名密钥进行数字签名的��|��及自��q��代码�{��证书。文件的接受者不仅能验证文�g的完整性,�q�可以依据自己对证书�{�֏�者和证书拥有者的信�Q�E�度�Q�决定是否接受该文�g。浏览器在下载运行插件和java���程序时�Q���用的���是�q�样的模式�?/p>
�W�二是用作保存二�q�制文�g�pȝ��的数字指�U�,以便������文件系�l�是否未�l�允许的被修攏V��不���系�l�管�?�pȝ��安全软�g都提供这一文�g�pȝ��完整性评估的功能�Q�在�pȝ��初始安装完毕后,建立�Ҏ��件系�l�的基础校验和数据库�Q�因为散列校验和的长度很���,它们可以方便的被存放在容量很���的存储介质上。此后,可以定期或根据需要,再次计算文�g�pȝ��的校验和�Q�一旦发��C��原来保存的值有不匹配,说明该文件已�l�被非法修改�Q�或者是被病毒感染,或者被木马�E�序替代。TripWire���提供了一个此�c�d��用的典型例子�?/p>
更完���的�Ҏ��是���?MAC"�?MAC" 是一个与Hash密切相关的名词,即信息鉴权码(Message Authority Code)。它是与密钥相关的Hash��|��必须拥有该密钥才能检验该Hash倹{��文件系�l�的数字指纹也许会被保存在不可信�ȝ��介质上,只对拥有该密钥者提供可鉴别性。�ƈ且在文�g的数字指�UҎ��可能需要被修改的情况下�Q�只有密钥的拥有者可以计���出新的散列��|��而企囄���坏文件完整性者却不能得逞�?/p>
2) 数字�{��
Hash ���法也是��C��密码体系中的一个重要组成部分。由于非对称���法的运���速度较慢�Q�所以在数字�{��协议中,单向散列函数扮演了一个重要的角色�?/p>
在这�U�签名协议中�Q�双方必���M��先协商好双方都支持的Hash函数和签名算法�?/p>
�{��方先对该数据文�g�q�行计算其散列��|��然后再对很短的散列值结�?-如Md5�?6个字节,SHA1�?0字节�Q�用非对�U�算法进行数字签名操作。对方在验证�{���Ӟ��也是先对该数据文件进行计���其散列��|��然后再用非对�U�算法验证数字签名�?/p>
�?Hash ��|��又称"数字摘要"�q�行数字�{���Q�在�l�计上可以认��Z���Ҏ��件本�w�进行数字签名是�{�效的。而且�q�样的协议还有其他的优点�Q?/p>
首先�Q�数据文件本�w�可以同它的散列值分开保存�Q�签名验证也可以��q��数据文�g本��n的存在而进行�?/p>
再者,有些情况下签名密钥可能与解密密钥是同一个,也就是说�Q�如果对一个数据文件签名,与对其进行非对称的解密操作是相同的操作,�q�是相当危险的,恶意的破坏者可能将一个试��N��你将其解密的文�g�Q�充当一个要求你�{��的文件发送给你。因此,在对��M��数据文�g�q�行数字�{���Ӟ��只有对其Hash��D��行签名才是安全的�?/p>
3) 鉴权协议
如下的鉴权协议又被称�?挑战--认证模式�Q�在传输信道是可被侦听,但不可被���改的情况下�Q�这是一�U�简单而安全的�Ҏ���?/p>
需要鉴权的一方,向将被鉴权的一方发送随��Z���Q?#8220;挑战”�Q�,被鉴权方���该随机串和自己的鉴权口令字一赯����?Hash �q�算后,�q�还鉴权方,鉴权方将收到的Hash��g��在己端用该随��Z��和对方的鉴权口��o字进�?Hash �q�算的结果相比较�Q?#8220;认证”�Q�,如相同,则可在统计上认�ؓ�Ҏ��拥有该口令字�Q�即通过鉴权�?/p>
POP3协议中就有这一应用的典型例子:
S: +OK POP3 server ready <1896.697170952@dbc.mtview.ca.us>
C: APOP mrose c4c9334bac560ecc979e58001b3e22fb
S: +OK maildrop has 1 message (369 octets)
在上面的一�D�POP3协议会话中,双方都共享的对称密钥�Q�鉴权口令字�Q�是tanstaaf�Q�服务器发出的挑战是<1896.697170952@dbc.mtview.ca.us>�Q�客��L���Ҏ��战的应答是MD5("<1896.697170952@dbc.mtview.ca.us>tanstaaf") = c4c9334bac560ecc979e58001b3e22fb�Q�这个正���的应答使其通过了认证�?/p>
散列���法长期以来一直在计算机科学中大量应用�Q�随着��C��密码学的发展�Q�单向散列函数已�l�成��Z��息安全领域中一个重要的�l�构模块�Q�我们有理由深入研究其设计理论和应用�Ҏ���?/p>







 }
} }
}