#
【描述】
“漢諾塔”,是一個眾所周知的古老游戲。現在我們把問題稍微改變一下:如果一共有4根柱子,而不是3根,那么至少需要移動盤子多少次,才能把所有的盤子從第1根柱子移動到第4根柱子上呢?
為了編程方便,您只需要輸出這個結果mod 10000的值。
【輸入】
一個正整數n。(0<n<=50000)
【輸出】
一個正整數,表示把n個盤子從第1根柱子移動到第4根柱子需要的最少移動次數mod 10000的值。
【樣例輸入】
15
【樣例輸出】
129
【分析】
弄出前幾個數,發現規律。
f[1]=1,之后分別是加2個2,加3個4,加4個8,加5個16……
1: #include <stdio.h>
2: #define maxn 50010
3:
4: int a,b;
5: int k=1,t;
6: long long j=1;
7: int n;
8:
9: int main()
10: {
11: freopen("hnoi.in","r",stdin);
12: freopen("hnoi.out","w",stdout);
13:
14: scanf("%d",&n);
15: b=1;
16: for (int i=2;i<=n;++i)
17: {
18: a=b;
19: if (!t)
20: {
21: t=++k;
22: j*=2;
23: j%=10000;
24: }
25: b=(a+j)%10000;
26: --t;
27: }
28: printf("%d\n",b);
29: return 0;
30: }
31:
【試題描述】
小FF的第一片礦區已經開始運作了, 他著手開展第二片礦區……
小FF的第二片礦區, 也是”NewBe_One“計劃的核心部分, 因為在這片礦區里面有全宇宙最稀有的兩種礦物,科學家稱其為NEW礦和BE礦。
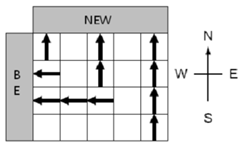
礦區是被劃分成一個n*m的矩形區域。 小FF探明了每一小塊區域里的NEW礦和BE礦的蘊藏量, 并且小FF還在礦區的北邊和西邊分別設置了NEW礦和BE礦的收集站。你的任務是設計一個管道運輸系統,使得運送的NEW礦和BE礦的總量最多。
管道的型號有兩種,一種是東西向,一種是南北向。在一個格子內你能建造一種管道,但丌能兩種都建。如果兩個同類型管道首位相接,它們就可以被連接起來。
另外這些礦物都十分丌穩定,因此它們在運送過程中都丌能拐彎。這就意味著如果某個格子上建有南北向管道,但是它北邊的格子建有東西向管道,那么這根南北向管道內運送的任何東西都將丟失。迚一步地,運到NEW礦收集站的BE礦也會丟失,運到BE礦收集站的NEW礦也會丟失。
【輸入格式】
第一行包含兩個整數n和m,表示礦區大小。
以下n行,每行m個整數,其中第i行第j個整數G[ i , j ] 描述各個格子上的BE礦數量。接下來以類似的矩陣表示各個格子上的NEW礦數量。
【輸出格式】
僅一個整數, 表示最多可以采集到的NEW礦和BE礦的總量。
【輸入樣例】
4 4
0 0 10 9
1 3 10 0
4 2 1 3
1 1 20 0
10 0 0 0
1 1 1 30
0 0 5 5
5 10 10 10
【輸出樣例】
98
【數據范圍】
對于30%的數據: 0<= n,m <=100;
對于100%的數據: 0<= n, m <=1000;
0<= G[ i, j ] <=1000.
【分析】
每個點只有兩種狀態,放be的管道或者放new的管道。
1: #include <stdio.h>
2: #include <iostream>
3: #define maxn 1010
4: using namespace std;
5:
6: int g[maxn][maxn][2];
7: long long f[maxn][maxn][2];
8: int ne[maxn][maxn],be[maxn][maxn];
9: int n,m;
10:
11: int main()
12: {
13: freopen("industry.in","r",stdin);
14: freopen("industry.out","w",stdout);
15:
16: scanf("%d%d",&n,&m);
17: for (int i=1;i<=n;++i)
18: for (int j=1;j<=m;++j)
19: scanf("%d",&g[i][j][0]);
20: for (int i=1;i<=n;++i)
21: for (int j=1;j<=m;++j)
22: scanf("%d",&g[i][j][1]);
23: for (int i=1;i<=n;++i)
24: for (int j=1;j<=m;++j)
25: {
26: ne[i][j]=ne[i-1][j]+g[i][j][1];
27: be[i][j]=be[i][j-1]+g[i][j][0];
28: }
29: for (int i=1;i<=n;++i)
30: for (int j=1;j<=m;++j)
31: {
32: f[i][j][0]=be[i][j]+max(f[i-1][j][0],f[i-1][j][1]);
33: f[i][j][1]=ne[i][j]+max(f[i][j-1][1],f[i][j-1][0]);
34: }
35: printf("%lld\n",max(f[n][m][1],f[n][m][0]));
36: return 0;
37: }
38:
【描述】
中國古代的歷史故事“田忌賽馬”是為大家所熟知的。話說齊王和田忌又要賽馬了,他們各派出N匹馬,每場比賽,輸的一方將要給贏的一方200兩黃金,如果是平局的話,雙方都不必拿出錢。現在每匹馬的速度值是固定而且已知的,而齊王出馬也不管田忌的出馬順序。請問田忌該如何安排自己的馬去對抗齊王的馬,才能贏取最多的錢?
【輸入】
第一行為一個正整數n (n <= 2000) ,表示雙方馬的數量。
第二行有N個整數表示田忌的馬的速度。
第三行的N個整數為齊王的馬的速度。
【輸出】
僅有一行,為田忌賽馬可能贏得的最多的錢,結果有可能為負。
【樣例輸入】
3
92 83 71
95 87 74
【樣例輸出】
200
【分析】
如果齊王的馬是按速度排序之后,從高到低被派出的話,田忌一定是將他馬按速度排序之后,從兩頭取馬去和齊王的馬比賽。
n設f[i,j]表示齊王按從強到弱的順序出馬和田忌進行了i場比賽之后,從“頭”取了j匹較強的馬,從“尾”取了i-j匹較弱的馬,所能夠得到的最大盈利。
n狀態轉移方程如下:
nF[I,j]=max{f[i-1,j]+g[n-(i-j)+1,i],f[i-1,j-1]+g[j,i]}
n其中g[i,j]表示田忌的馬和齊王的馬分別按照由強到弱的順序排序之后,田忌的第i匹馬和齊王的第j匹馬賽跑所能取得的盈利,勝為200,輸為-200,平為0。
1: #include <stdio.h>
2: #include <limits.h>
3: #include <stdlib.h>
4: #define maxn 1010
5:
6: int a[maxn],b[maxn];
7: int g[maxn][maxn];
8: int f[2][maxn];
9: int n,er;
10: int ans;
11:
12: int cmp(const void*a,const void*b)
13: {
14: int c=*(int*)a,d=*(int*)b;
15: if (c<d) return 1;
16: if (c>d) return -1;
17: return 0;
18: }
19:
20: int main()
21: {
22: scanf("%d",&n);
23: for (int i=1;i<=n;++i) scanf("%d",&b[i]);
24: for (int i=1;i<=n;++i) scanf("%d",&a[i]);
25: a[0]=b[0]=INT_MAX;
26: qsort(a,n+1,sizeof(int),cmp);
27: qsort(b,n+1,sizeof(int),cmp);
28: for (int i=1;i<=n;++i)
29: for (int j=1;j<=n;++j)
30: if (a[i]>b[j]) g[i][j]=-200;
31: else
32: if (a[i]<b[j]) g[i][j]=200;
33: for (int i=1;i<=n;++i)
34: {
35: er^=1;
36: for (int j=0;j<=i;++j)
37: {
38: f[er][j]=f[er^1][j]+g[i][n-i+j+1];
39: if (j)
40: if (f[er^1][j-1]+g[i][j]>f[er][j])
41: f[er][j]=f[er^1][j-1]+g[i][j];
42: }
43: }
44: for (int i=0;i<=n;++i)
45: if (f[er][i]>ans)
46: ans=f[er][i];
47: printf("%d\n",ans);
48: return 0;
49: }
50:
今天上午講的是線性的動歸。講的例題有:
- 機器分配模型
- 船
- 樓梯問題
- 田忌賽馬
- 最長公共子串
然后就是有關矩形的動態規劃。如下:
- 滑雪
- 工業時代
還有區間類的:
- 凸多邊形劃分
- 最大乘積
- 石子合并(用到了四邊形不等式)
- 數字游戲
然后有三道測試題:
- 四塔問題
- 關燈
- 任務安排
下午開始將樹形的動態規劃。
- 聚會的快樂
- 三色二叉樹
- 皇宮看守
- 珠寶
- 符文之旅(最小與最大)
沒有寫的題目以后會逐步完成。
【問題描述】
一棵二叉樹可以按照如下規則表示成一個由0、1、2 組成的字符序列,我們稱之為“二叉樹序列S”:
2表示該樹有兩個子節點, 和分別表示其兩個子樹的二叉樹序列
1表示該樹有一個子節點, 為其子樹的二叉樹序列
0表示該樹沒有子節點
你的任務是要對一棵二叉樹的節點進行染色。每個節點可以被染成紅色、綠色或藍色。并且,一個節點與其子節點的顏色必須不同,如果該節點有兩個子節點,那么這兩個子節點的顏色也必須不相同。給定一棵二叉樹的二叉樹序列,請求出這棵樹中最多和最少有多少個點能夠被染成綠色。
【輸入文件】
輸入文件名:TRO.IN
輸入文件僅有一行,不超過10000 個字符,表示一個二叉樹序列。
【輸出文件】
輸出文件名:TRO.OUT
輸出文件也只有一行,包含兩個數,依次表示最多和最少有多少個點能夠被
染成綠色。
【樣例輸入】
1122002010
【樣例輸出】
5 2
【分析】
1.動歸分析
拿最大來說。
每個節點的狀態只有三種顏色,我們用f[i][0],f[i][1]分別代表第i個點染綠色和不然綠色的最多的點數。因為如果一個點不染綠色,那么他染另兩種顏色是等價的。如此我們就得到了如下的動規方程:
- 葉子:f[i][0]=1; f[i][1]=0;
- 一個子節點:f[i][0]=f[子節點][1]; f[i][1]=max(f[子節點][0],f[子節點][1]);
- 兩個子節點:f[i][0]=f[左兒子][1]+f[右兒子][1]; f[i][1]=max(f[左兒子][1]+f[右兒子][0],f[左兒子][0]+f[右兒子][1]);
最后輸出就是max(f[0][1],f[0][0])。
最小的和最大的相同。
2.樹的確定
因為是一棵二叉樹的前序遍歷,那么對于一個有子節點的點來說,左兒子就是i+1。我們引進一個link[i],表示以i為根的子樹最后一個點的標號,那么r[i]=link[l[i]]+1。
對于link[l],我們如此確定:
- 葉子:link[l]=l;
- 一個子節點:link[l]=link[l+1];
- 兩個子節點:link[l]=link[link[l+1]+1];
然后就是實現了。因為自己弄得還是不是很熟,打了兩節課。
1: #include <stdio.h>
2: #include <string.h>
3: #include <iostream>
4: #define maxn 10010
5: #define MAXINT 10000000
6: using namespace std;
7:
8: char s[maxn];
9: int f[maxn][2];
10: int link[maxn];
11: int n;
12: int l[maxn],r[maxn];
13:
14: int _find(int x)
15: {
16: if (link[x]) return link[x];
17: if (s[x]=='0') link[x]=x;
18: else
19: if (s[x]=='1') link[x]=_find(x+1);
20: else
21: link[x]=_find(_find(x+1)+1);
22: return link[x];
23: }
24:
25: void find1(int x)
26: {
27: if (f[x][0]) return;
28: if (s[x]=='0')
29: {
30: f[x][0]=1;
31: f[x][1]=0;
32: }
33: else
34: if (s[x]=='1')
35: {
36: find1(l[x]);
37: f[x][0]=f[l[x]][1]+1;
38: f[x][1]=max(f[l[x]][1],f[l[x]][0]);
39: }
40: else
41: {
42: find1(l[x]);
43: find1(r[x]);
44: f[x][0]=f[l[x]][1]+f[r[x]][1]+1;
45: f[x][1]=max(f[l[x]][1]+f[r[x]][0],f[l[x]][0]+f[r[x]][1]);
46: }
47: }
48:
49: void find2(int x)
50: {
51: if (f[x][0]<MAXINT) return;
52: if (s[x]=='0')
53: {
54: f[x][0]=1;
55: f[x][1]=0;
56: }
57: else
58: if (s[x]=='1')
59: {
60: find2(l[x]);
61: f[x][0]=f[l[x]][1]+1;
62: f[x][1]=min(f[l[x]][1],f[l[x]][0]);
63: }
64: else
65: {
66: find2(l[x]);
67: find2(r[x]);
68: f[x][0]=f[l[x]][1]+f[r[x]][1]+1;
69: f[x][1]=min(f[l[x]][1]+f[r[x]][0],f[l[x]][0]+f[r[x]][1]);
70: }
71: }
72:
73: int main()
74: {
75: freopen("tro.in","r",stdin);
76: freopen("tro.out","w",stdout);
77:
78: scanf("%s",s);
79: n=strlen(s);
80: _find(0);
81: for (int i=0;i<n;++i)
82: {
83: l[i]=i+1;
84: r[i]=link[l[i]]+1;
85: }
86: find1(0);
87: printf("%d ",max(f[0][0],f[0][1]));
88: for (int i=0;i<n;++i)
89: f[i][0]=f[i][1]=MAXINT;
90: find2(0);
91: printf("%d\n",min(f[0][0],f[0][1]));
92: return 0;
93: }
94:
題目網上都可以找到。
注意初始化s[i][j]的時候要加上100000而不是10!!!我傻叉子了= =
1: #include <stdio.h>
2: #define MAXINT 10000000
3: #define maxn 200
4:
5: int f[maxn][maxn][maxn][2];//0 max|||| 1 min
6: int s[maxn][maxn];
7: int a[maxn];
8: int n,m;
9: int maxans,minans=MAXINT;
10:
11: void find(int x,int y,int t)
12: {
13: if (f[x][y][t][0]) return;
14: if (t==1)
15: {
16: f[x][y][1][0]=f[x][y][1][1]=s[x][y];
17: return;
18: }
19: for (int k=x+t-1-1;k<y;++k)
20: {
21: find(x,k,t-1);
22: if (f[x][k][t-1][1]*s[k+1][y]<f[x][y][t][1]) f[x][y][t][1]=f[x][k][t-1][1]*s[k+1][y];
23: if (f[x][k][t-1][0]*s[k+1][y]>f[x][y][t][0]) f[x][y][t][0]=f[x][k][t-1][0]*s[k+1][y];
24: }
25: }
26:
27: int main()
28: {
29: freopen("game.in","r",stdin);
30: freopen("game.out","w",stdout);
31:
32: scanf("%d%d",&n,&m);
33: for (int i=1;i<=n;++i)
34: {
35: scanf("%d",&a[i]);
36: a[i+n]=a[i];
37: }
38: for (int i=1;i<=2*n;++i)
39: for (int j=i;j<=2*n;++j)
40: for (int k=1;k<=m;++k)
41: f[i][j][k][1]=MAXINT;
42: for (int i=1;i<=2*n;++i)
43: for (int j=i;j<=2*n;++j)
44: s[i][j]=(s[i][j-1]+a[j]+100000)%10;
45: for (int i=1;i<=n;++i) find(i,i+n-1,m);
46: for (int i=1;i<=n;++i)
47: {
48: if (f[i][i+n-1][m][0]>maxans) maxans=f[i][i+n-1][m][0];
49: if (f[i][i+n-1][m][1]<minans) minans=f[i][i+n-1][m][1];
50: }
51: printf("%d\n%d\n",minans,maxans);
52: return 0;
53: }
54:
【題目描述】
尋找一個由n個整數組成的數列,其中任意連續p個整數之和為正,任意連續q個整數之和為負。若不存在這樣的整數數列,則輸出NO,否則輸出其中一個數列。
【輸入】
對于每個測試點將給你M組數據,要求你對于每組數據,判斷是否存在這樣的整數數列。
輸入的第一行是一個正整數M,(1<=N<=10000),接下來的M行對應M組數據,每行有三個正整數N、P、Q(1<=n,p,q<=10^8)。
【輸出】
輸出數據共N行,每行為yes或者no,如果第I組數據有解,則在第I行輸出yes,否則輸出no
【輸入輸出示例】
| 輸入(sequence.in) | 輸出(sequence.out) |
2
1 1 9
10 2 4 | yes
no |
【評分標準】
對于每個測試點,如果你能夠在1S內通過每組數據,你將得到這個測試點的分數,否則,這個測試點你只能得0分。
【分析】
原題目是要求輸出一種可能的解,如果沒有解就輸出-1。這樣的話就要用到差分約束。
現在的話,只需要一個公式。如果有解,應滿足:n<=q+p-gcd(p,q)-1。
1: #include <stdio.h>
2: #include <iostream>
3: using namespace std;
4:
5: int n,m,p,q;
6:
7: int gcd(int a,int b)
8: {
9: if (a<b) swap(a,b);
10: int t;
11: while (b!=0)
12: {
13: t=a;
14: a=b;
15: b=t%a;
16: }
17: return a;
18: }
19:
20: int main()
21: {
22: freopen("sequence.in","r",stdin);
23: freopen("sequence.out","w",stdout);
24:
25: scanf("%d",&m);
26: for (int i=0;i<m;++i)
27: {
28: scanf("%d%d%d",&n,&p,&q);
29: if (n<=p+q+gcd(p,q)-1) printf("YES\n");
30: else printf("NO\n");
31: }
32: return 0;
33: }
34:
下面是我寫的查分約束。
1: #include <stdio.h>
2: #define MAXINT 1000000
3: #define maxn 1010
4:
5: struct ss
6: {
7: int x,y,dis;
8: } l[10000];
9:
10: int s[maxn];
11: int a[maxn];
12: int d[maxn];
13: int n,q,p,tot;
14:
15: int main()
16: {
17: scanf("%d%d%d",&n,&p,&q);
18: for (int i=0;i<=n;++i)
19: if (i+p>n) break;
20: else
21: {
22: l[++tot].x=i+p;
23: l[tot].y=i;
24: l[tot].dis=-1;
25: }
26: for (int i=0;i<=n;++i)
27: if (i+q>n) break;
28: else
29: {
30: l[++tot].x=i;
31: l[tot].y=i+q;
32: l[tot].dis=-1;
33: }
34: for (int i=1;i<=n;++i)
35: {
36: for (int j=1;j<=tot;++j)
37: if (d[l[j].y]>d[l[j].x]+l[j].dis)
38: d[l[j].y]=d[l[j].x]+l[j].dis;
39: for (int j=1;j<=tot;++j)
40: if (d[l[j].y]>d[l[j].x]+l[j].dis)
41: {
42: printf("-1\n");
43: return 0;
44: }
45: }
46: for (int i=0;i<=n;++i)
47: s[i]=d[i];
48: for (int i=1;i<=n;++i) printf("%d\n",s[i]-s[i-1]);
49: return 0;
50: }
51:
今天上午從東區搬東西到西區。11點都收拾完了,然后到水房潑了一個小時的水。
下午兩點多的時候曹老師開始講課。
今天的課程是兩個內容:全面分析試題,動態規劃。
曹老師拿他給自己的學生布置的任務做例子,大概的說了一下從一個題目的模型到完整的題目的過程。首先曹老師給了4道題目,都只是大概的描述。然后將每個條件定嚴謹。確定輸入輸出的格式。分析可以用什么算法,每種算法的時間復雜度以及可以通過的數據范圍。根據算法定出數據,寫出標程。曹老師說他們的學生每個人通過自己的分析,做出10個數據,然后大概100多個測試點來測試每個人寫的程序。
以下是4道題目。第二題有些瓶頸,一會再發。
- 動態規劃-走迷宮問題
- 空缺
- 貪心-買彩票
- 數學問題-Black and White
【題目描述】
尋找一個由n個整數組成的數列,其中任意連續p個整數之和為正,任意連續q個整數之和為負。若不存在這樣的整數數列,則輸出NO,否則輸出其中一個數列。
【輸入】
對于每個測試點將給你M組數據,要求你對于每組數據,判斷是否存在這樣的整數數列。
輸入的第一行是一個正整數M,(1<=N<=10000),接下來的M行對應M組數據,每行有三個正整數N、P、Q(1<=n,p,q<=10^8)。
【輸出】
輸出數據共N行,每行為yes或者no,如果第I組數據有解,則在第I行輸出yes,否則輸出no
【輸入輸出示例】
| 輸入(sequence.in) | 輸出(sequence.out) |
2
1 1 9
10 2 4 | yes
no |
【評分標準】
對于每個測試點,如果你能夠在1S內通過每組數據,你將得到這個測試點的分數,否則,這個測試點你只能得0分。
【分析】
原題目是要求輸出一種可能的解,如果沒有解就輸出-1。這樣的話就要用到差分約束。
現在的話,只需要一個公式。如果有解,應滿足:n<=q+p+gcd(p,q)-1。
1: #include <stdio.h>
2: #include <iostream>
3: using namespace std;
4:
5: int n,m,p,q;
6:
7: int gcd(int a,int b)
8: {
9: if (a<b) swap(a,b);
10: int t;
11: while (b!=0)
12: {
13: t=a;
14: a=b;
15: b=t%a;
16: }
17: return a;
18: }
19:
20: int main()
21: {
22: freopen("sequence.in","r",stdin);
23: freopen("sequence.out","w",stdout);
24:
25: scanf("%d",&m);
26: for (int i=0;i<m;++i)
27: {
28: scanf("%d%d%d",&n,&p,&q);
29: if (n<=p+q+gcd(p,q)-1) printf("YES\n");
30: else printf("NO\n");
31: }
32: return 0;
33: }
34:
【問題描述】
電視里面正放著“抽百萬大獎,贏幸福生活”的宣傳廣告,bird看后也想去試試手氣,當然,作為經濟學院的高材生,他可不屑只是單純的去碰運氣。經過他的一番分析,發現,商家在彩票里面做了手腳,使得每個抽獎點的中獎概率不是完全一樣的,而且隨著時間的變化而變化,不過這種變化是有規律的。對于第I個抽獎點,最開始的中獎概率是百萬分之Pi,以后每抽一張彩票后都要重新排隊,花費的時間是T分鐘,每抽一次減少的概率為Di。
由于可憐的bird還有一大堆的作業沒做,他只能抽出H個小時去買彩票。由于抽獎地點都在一路公共汽車的線路上,所以怕麻煩的bird決定按車站順序抽獎,當然,bird可以從任意一站開始抽獎,對于經過的抽獎點可以買彩票,也可以不買。假設從第I個抽獎點到第I+1個抽獎點需要做Ci分鐘的汽車。
Bird希望能在有限的H個小時內獲得最好的運氣——即抽獎的概率和最大。
[輸入] 輸入文件名:(tickt.in)
第一行為一個整數n,表示抽獎點的個數,1<=n<=200
第二行是兩個整數H和T,1<=H<=10,1<=T<=60。
接下來的n行,每行3個整數,分別是Pi,Di,Ci(Cn=0)。1<=Pi<=10000,Di<=Pi,1<=Ci<=600。
[輸出] 輸出文件名:(tickt.out)
文件僅有一行,為一個整數,即抽獎概率和的最大值。
【輸入輸出樣例】
| tickt.in | tickt.out |
| 2 1 20 200 100 10 300 200 0 | 500 |
【樣例說明】
首先,bird從1號開始抽獎,花費20分鐘,得到概率200,然后坐車到2號,花費10分鐘,再花20分鐘得到概率300,概率和是500,花費50分鐘。
【評分標準】
對于每個測試點,如果你能夠在規定的時間內通過每組數據,你將得到這個測試點的分數,否則,這個測試點你只能得0分。
【分析】
由CEOI的釣魚改編,具體可以看《算法藝術與信息學競賽》P13。
1: #include <stdio.h>
2: #include <iostream>
3: #define maxn 210
4: using namespace std;
5:
6: int b[maxn][maxn];
7: int p[maxn],d[maxn],c[maxn];
8: int h,t,tot;
9: struct ss
10: {
11: int pi,di;
12: } hp[maxn];
13: int remain,ans,teans,n;
14:
15: void down(int x)
16: {
17: int te=2*x;
18: while (te<=tot)
19: {
20: if ((te+1<=tot)&&(hp[te].pi<hp[te+1].pi)) ++te;
21: if (hp[x].pi>hp[te].pi) break;
22: swap(hp[x],hp[te]);
23: x=te;
24: te=x*2;
25: }
26: }
27:
28: int main()
29: {
30: freopen("ticket.in","r",stdin);
31: freopen("ticket.out","w",stdout);
32:
33: scanf("%d%d%d",&n,&h,&t);
34: h*=60;
35: for (int i=1;i<=n;++i) scanf("%d%d%d",&p[i],&d[i],&c[i]);
36: for (int i=1;i<=n;++i)
37: for (int j=i+1;j<=n;++j)
38: b[i][j]=b[i][j-1]+c[j-1];
39: for (int i=1;i<=n;++i)
40: for (int j=n;j>=i;--j)
41: {
42: teans=0;
43: remain=h-b[i][j];
44: memset(hp,0,sizeof(hp));
45: for (int k=1;k<=j-i+1;++k)
46: {
47: hp[k].pi=p[i+k-1];
48: hp[k].di=d[i+k-1];
49: }
50: tot=j-i+1;
51: for (int k=j-i+1;k>=1;--k) down(k);
52: while ((remain>=t)&&(hp[1].pi>0))
53: {
54: teans+=hp[1].pi;
55: hp[1].pi-=hp[1].di;
56: remain-=t;
57: down(1);
58: }
59: if (teans>ans) ans=teans;
60: }
61: printf("%d\n",ans);
62: return 0;
63: }
64: