| Time Limit: 3000MS | Memory Limit: 30000K | |
| Total Submissions: 5123 | Accepted: 1393 |
Description
Hugo Heavy is happy. After the breakdown of the Cargolifter project he can now expand business. But he needs a clever man who tells him whether there really is a way from the place his customer has build his giant steel crane to the place where it is needed on which all streets can carry the weight.
Fortunately he already has a plan of the city with all streets and bridges and all the allowed weights.Unfortunately he has no idea how to find the the maximum weight capacity in order to tell his customer how heavy the crane may become. But you surely know.
Problem
You are given the plan of the city, described by the streets (with weight limits) between the crossings, which are numbered from 1 to n. Your task is to find the maximum weight that can be transported from crossing 1 (Hugo's place) to crossing n (the customer's place). You may assume that there is at least one path. All streets can be travelled in both directions.
Input
Output
Sample Input
1 3 3 1 2 3 1 3 4 2 3 5
Sample Output
Scenario #1: 4 ĺlôŚģönšł™ÁāĻŚQĆŚŹämśĚ°ŤĺĻÁöĄśúÄŚ§ßŤīüŤĹĹԾƜĪāť°∂Áā?Śąįť°∂ÁāĻnÁöĄśúÄŚ§ßśĶĀ„Ä?/pre>ÁĒ®DijkstraĹéóś≥ēŤß£šĻčŚQĆŚŹ™śėĮťúÄŤ¶Āśää“śúÄÁü≠ŤĶ\”ÁöĄŚģöšĻČÁ®ćŚĺģśĒĻŚŹėšłÄšłčÔľĆAŚąįBÁöĄŤĶ\ťēŅŚģöšĻČšōďŤ∑ĮŚĺĄšłäŤĺĻśĚÉśúÄěģŹÁöĄťā£śĚ°ŤĺĻÁöĄťēŅŚļ¶ŚQ?/pre>ŤÄĆśúÄÁü≠ŤĶ\ŚÖ∂ŚģěśėĮAŚąįBśČÄśúČŤĶ\ťēŅÁöĄśúÄŚ§ßŚÄĻ{Ä?/pre>//Heavy Transportation
//Dijkstra
#include <iostream>
#include<stdio.h>
using namespace std;
const int MAXS=1005;
int n;
int mat[MAXS][MAXS];
int asd[MAXS];
int s[MAXS];
int min(int a,int b)
{return a<b?a:b;}
int Dijkstra()
{
int i,j;
for(i=1;i<n;i++)

{
asd[i]=mat[0][i];
s[i]=0;
}
s[0]=1;
asd[0]=0;
for(i=0;i<n-1;i++)

{
int max=0;
int u=0;
for(j=1;j<n;j++)

{
if(s[j]==0 && asd[j]>max)

{
u=j;
max=asd[j];
}
}
if(u==0)
break;
s[u]=1;
asd[u]=max;
for(j=1;j<n;j++)

{
if (s[j]==0 && asd[j]<min(asd[u],mat[u][j]))

{
asd[j]=min(asd[u],mat[u][j]);

}
}
}
return asd[n-1];
}
int main()
{

int t,m;
int i,j;
scanf("%d",&t);
int v1,v2;
int value;
for (int s=1;s<=t;s++)

{
scanf("%d%d",&n,&m);
for(i=0;i<n;i++)
for (j=0;j<n;j++)

{
mat[i][j]=0;
}
while (m--)

{
scanf("%d%d%d",&v1,&v2,&value);
mat[v1-1][v2-1]=mat[v2-1][v1-1]=value;

}
printf("Scenario #%d:\n%d\n\n",s,Dijkstra());
}
return 0;
}
Ťč•šĹô 2010-09-01 09:28 ŚŹĎŤ°®ŤĮĄŤģļ]]>
| Time Limit: 1000MS | Memory Limit: 65536K | |
| Total Submissions: 720 | Accepted: 201 |
Description
Panda has received an assignment of painting a line of blocks. Since Panda is such an intelligent boy, he starts to think of a math problem of painting. Suppose there are N blocks in a line and each block can be paint red, blue, green or yellow. For some myterious reasons, Panda want both the number of red blocks and green blocks to be even numbers. Under such conditions, Panda wants to know the number of different ways to paint these blocks.
Input
The first line of the input contains an integer T(1≤T≤100), the number of test cases. Each of the next T lines contains an integer N(1≤N≤10^9) indicating the number of blocks.
Output
For each test cases, output the number of ways to paint the blocks in a single line. Since the answer may be quite large, you have to module it by 10007.
Sample Input
2 1 2
Sample Output
2 6
Source
ĺlôŚģöšłÄŚĚóśúČnšł™ÁāĻÁöĄśú®ŚĚóÔľĆÁĒ®ŚõõŅUćťĘúŤČ≤ś∂āŤČ‘ƾƌÖ∂šł≠šł§ÁßćťĘúŤČ≤ŚŹ™ŤÉĹÁĒ®ŚĀ∂śēįś¨°ŚQĆśĪāśúČŚ§öěģĎÁßćś∂āŤČ≤śĖ“é≥ē„Ä?br>
šłÄÁúčŚįĪÁü•śėĮÁĒüśąźŚáĹśēįŚQĆŚŹĮśÉúšĽéś≤°ÁĒ®ėqá„ÄāŚįŹŤĮēŤŪnśČčԾƜ≤°śÉ≥ŚąįÁęüÁĄ∂ŚľĄŚáļśĚ•šļÜ„ÄāÁĽďśěúŚļĒŤĮ•śėĮŚĮĻÁöĄŚQĆŚįĪśėĮšłćÁü•ŤŅáĹEčśėĮšłćśėĮŚŹĮšĽ•ėqôś†∑ŚÜô„Ä?br>ŤģĎ÷õõŅUćťĘúŤČ≤ŚąÜŚąęšōďwŚQĆxŚQĆyŚQĆzŚQĆŚÖ∂šł≠yŚQĆzŚŹ™ŤÉĹÁĒ®ŚĀ∂śēįś¨°ŚQĆśąĎÁöĄśé®ŚĮ∆DŅáĹE茶āšłčÔľö
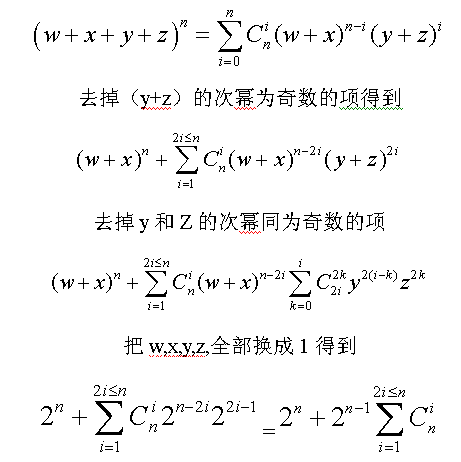
śúÄŚźéŚĺóŚąįÁöĄŚÖ¨ŚľŹśė?2^( n - 1 ))(2^(n-1)+1)
ś≥®śĄŹŚą?0007śėĮÁī†śē?ÁĒřpīĻěģĒť©¨ŚģöÁźÜ,ŚŹĮšĽ•ŚÖąśään-1modŚQ?0007-1ŚQ?ŚáŹŚįŹŤģ°Áģóťá?ŚČ©šłčÁöĄŚįĪśėĮŚŅęťÄüŚŹĖÚqāšļÜ.
 #include <iostream>
#include <iostream> using namespace std;
using namespace std; const int mod=10007;
const int mod=10007; int pow(int n)
int pow(int n)

 {
{ if(n==0)
if(n==0) return 1;
return 1; if(n&1)
if(n&1)

 {
{ return (pow(n-1)<<1)%mod;
return (pow(n-1)<<1)%mod; }
} else
else

 {
{ int temp=pow(n>>1);
int temp=pow(n>>1); return (temp*temp)%mod;
return (temp*temp)%mod; }
} }
}
 int main(int argc, char *argv[])
int main(int argc, char *argv[])

 {
{ int t,n,temp;
int t,n,temp; cin>>t;
cin>>t; while(t--)
while(t--)

 {
{ cin>>n;
cin>>n; temp=pow((n-1)%(mod-1));
temp=pow((n-1)%(mod-1)); cout<<(temp*(temp+1))%mod<<endl;
cout<<(temp*(temp+1))%mod<<endl; }
}
 return 0;
return 0; }
}
| Time Limit: 1000MS | Memory Limit: 65536K | |
| Total Submissions: 4525 | Accepted: 1849 |
Description
25 7
11 7
4 7
4 3
1 3
1 0
an Stan wins.
Input
Output
Sample Input
34 12 15 24 0 0
Sample Output
Stan wins Ollie wins
Source
ĺlôŚģöšł§Ś†ÜÁüõ_≠ź,šļĆšĚhŤĹģśĶĀŚŹĖŚ≠ź,Ť¶ĀśĪāŚŹ™ŤÉĹšĽéÁü≥Ś≠źśēįÁõģŤĺÉŚ§ßÁöĄťā£šłÄŚ†ÜŚŹĖŚ≠?ŚŹĖŚ≠źÁöĄśēįÁõģŚŹ™ŤÉĹśėĮŚŹ¶šłÄŚ†ÜÁü≥Ś≠źśēįÁõģÁöĄŚÄćśēį.śúÄĺląšč…ŚĺóśüźšłÄŚ†ÜśēįÁõģšōďťõ∂ÁöĄšłÄśĖĻšōďŤÉ?
ť¶ĖŚÖą,Śģ“éėďÁúčŚáļ,ŚĮĻšļéśĮŹšłÄšł™ŚĪÄťĚ?Ť¶ĀšĻąśėĮŚÖąśČčŚŅÖŤÉ?Ť¶ĀšĻąśėĮŚźéśČčŚŅÖŤÉ?śúÄĺląÁĽďśěúŚģĆŚÖ®ÁĒĪŚĹďŚČćŚĪÄťĚĘŚģĆŚÖ®Á°ģŚģ?
ŚŹ¶Ś§Ė,ŚŹĮšĽ•ĹéÄŚćēÁĹóŚąóšłÄšłčŚÖąśČčŚŅÖŤÉúŚíĆŚŅÖŤ”|ÁöĄŚá†ŅUćŚĪÄťĚ?šł§Ś†ÜÁüõ_≠źŚąĚŚßčśēįÁõģťÉĹŚ§ßšļéťõ∂):
1,śúČšłÄŚ†ÜÁü≥Ś≠źśēįÁõģšōďšłÄ,ŚÖąśČčŚŅÖŤÉú,¬† 1,4,¬†¬†¬† 1,2.
2,šł§Ś†ÜÁüõ_≠źśēįÁõģŚ∑ģšłÄ,šłĒšł§Ś†ÜÁü≥Ś≠źśēįÁõģťÉĹšłćšōďšłÄ,ŚÖąśČčŚŅÖŤ”|(ŚŹ™ŤÉĹšĹŅŚźéśČčťĚĘŚĮĻŚŅÖŤÉúÁöĄŚĪÄťĚ?,Ś¶ā¬?3,4¬† 5,6¬†¬† .
3,Ś¶āśěúśēįÁõģŤĺÉŚ§ßÁöĄťā£šłÄŚ†ÜśėĮśēįÁõģŤĺÉŚįŹťā£šłÄŚ†ÜÁöĄ2ŚÄćŚä†ŚáŹšłÄ,šłĒšłćśėĮšłäťĚĘšł§ŅUćŚĪÄťĚ?ŚÖąśČčŚŅÖŤÉú,2,5¬† 3,5¬† 3,7.
ŚŹĮśėĮšłäťĚĘėqôšļõšŅ°śĀĮŚĮĻšļéŤß£ŚÜ≥ėqôšł™ťóģťĘėėqėśėĮśúČšłÄšļõŚõįťö?
ŚÜćŤŅõšłÄś≠•ŤĮēĹéóśēįÁõģŤĺÉěģŹÁöĄÁüõ_≠ź,ŚŹĮšĽ•ŚŹĎÁéį,ŚĹďšł§Ś†ÜśēįÁõģÁõłŚ∑ģŤĺÉŚ§ßśó∂,śÄņLėĮŚÖąśČčŚŅÖŤÉú.
šļčŚģěšł?ėqõšłÄś≠•śéĘŤģ®ŚŹĮšĽ•ŚŹĎÁéÓCłčťĚĘÁöĄĺlďŤģļ:
1,N<2*M-1śó?ŚÖąśČ茹ęśó†ťÄČśč©,ŚŹ™ŤÉĹšĹŅšĻ茏ėšōď N-M,M ŚĪÄťĚ?(śėďŤßĀ)Ś¶?,5¬† 5,7¬† 7,4...
2,Ťģĺšł§Ś†ÜÁü≥Ś≠źśēįÁõģšōďN,M(N>M>0,šłĒN,MšļíŤī®),ŚąôŤč•N>=2*M-1,šłĒN - M ! =1śó?ŚÖąśČčŚŅÖŤÉú.Ť¶ĀśĪāM,NšļíŤī®śėĮŚõ†šłļŚĮĻšļéM,NśúČŚÖ¨Śõ†śēįÁöĄśÉÖŚĹ?ŚŹĮšĽ•ŚźĆśó∂ťô§šĽ•ŚÖ∂ŚÖ¨Śõ†śēįŤÄĆšłćŚĹĪŚďćĺlďśěú.
ĹéÄŚćēŤĮīśė隳ĚłčšłäťĚĘÁĽďŤģ?ÁöĄÁĒĪśĚ? N>=2*M-1śó?ŚÖąśČ茏Įšč…šĻ茏ėšłļ¬?N%M,M¬† śąĖN%M+M,Mšł§ÁßćŚĪÄťĚĘšĻčšłÄ,ŚÖ∂šł≠śúČšłĒŚŹ™śúČšłÄšł™ŚŅÖŤī•ŚĪÄťĚĘ„Äāś≥®śĄŹŚąįŚ¶āśěúN%M,MšłćśėĮŚŅÖŤ”|ŚĪÄťĚĘԾƝā£šĻąN%M+M,MěģĪśėĮŚŅÖŤ”|ŚĪÄťĚĘԾƌõ†šōďťĚĘŚĮĻN%M+M,Mėqôšł™ŚĪÄťĚĘԾƚņŚąęśó†ťÄČśč©ŚQĆŚŹ™ŤÉĹŚú®ŚČ暳Ȇܚł≠ŚŹĖMšł™šč…ŚĮ“éĖĻťĚĘŚĮĻŚŅÖŤÉúŚĪÄťĚ?ĺlďŤģļ1 )„Ä?br />
śćģś≠§ŚŹĮŤģĺŤģ°Áģóś≥ēŚ¶āšł?
1.M,NŚÖąŚźĆśóČôô§šĽ•ŚģÉšĽ¨ÁöĄśúÄŚ§ßŚÖ¨Śõ†śēį.(M<N)
2,Ś¶āśěúM==0,ŚąôŤŅĒŚõěťõ∂;
3,Ś¶āśěúM==1,ŚąôŤŅĒŚõěšłÄ;
4,Ś¶āśěúN>=M*2-1,ŚąôŤŅĒŚõěšłÄ
5,šĽ§N=M,M=N-M,ťÄíŚĹ팧ĄÁźÜ
 #include <iostream>
#include <iostream> using namespace std;
using namespace std; long long gcd(long long a,long long b)
long long gcd(long long a,long long b)

 {
{     if(a==0)
    if(a==0)         return b;
        return b;     return gcd(b%a,a);
    return gcd(b%a,a); }
} long long Eu(long long m,long long n)
long long Eu(long long m,long long n)

 {
{     if(m==1)
    if(m==1)         return 1;
        return 1;     if(n-m==1 && m)
    if(n-m==1 && m)         return 0;
        return 0;     if(n>=m*2-1)
    if(n>=m*2-1)         return 1;
        return 1;     return !Eu(n%m,m);
    return !Eu(n%m,m); }
}
 int  main()
int  main()

 {
{     long long m,n,temp;
    long long m,n,temp;     while (cin>>m>>n && (m||n))
    while (cin>>m>>n && (m||n))
     
     {
{         long long g=gcd(m,n);
        long long g=gcd(m,n);         m/=g;
        m/=g;         n/=g;
        n/=g;         if(m>n)
        if(m>n)
         
         {
{             temp=m;
            temp=m;             m=n;
            m=n;             n=temp;
            n=temp;         }
        }         if(Eu(m,n))
        if(Eu(m,n))             cout<<"Stan wins"<<endl;
            cout<<"Stan wins"<<endl;         else
        else             cout<<"Ollie wins"<<endl;
            cout<<"Ollie wins"<<endl;     }
    }     
         return 0;
    return 0; }
}

| Time Limit: 10000MS | Memory Limit: 65536K | |
| Total Submissions: 6561 | Accepted: 2091 |
Description
Input
In (N+2)-th line, you'll get an integer M (1 <= M <= 50), which represents the number of exams. The following M parts each represent an exam. Each exam has N lines. In each line, there is a positive integer S, which is no more then 100, and a name P, which must occur in the name list described above. It means that in this exam student P gains S scores. It’s confirmed that all the names in the name list will appear in an exam.
Output
Sample Input
3 Li Ming A B 2 49 Li Ming 49 A 48 B 80 A 85 B 83 Li Ming
Sample Output
1 2
Source
ĺlôŚģöśĮŹšł™šļļÁöĄśąźÁáWŚQĆśü•ŤĮĘśüźšłÄšļļÁöĄŚźćś¨°„Ä?br />
ÁĒ®MAPŚĽļÁęčšļļŚźćŚíĆśąźĺl©ÁöĄŚĮĻŚļĒŚÖ≥Á≥ĽŚQĆÁĒ®cntśēįÁĽĄŚQąśúÄŚ§?000šł™ŚÖÉÁī†ÔľČŤģįŚĹēśąźÁáWšłļśüźšł™ŚąÜśēįÁöĄšļļśēįŚQĆšłćėqáÁĒĪšļéśÄ÷MĚhśēįŤĺÉěģ?śúÄŚ§öŚŹ™śú?0000šļ?,Áõīśé•ťĀćŚéÜšĻüšłćśĮĒŚĺŹÁęčŤģ°śēįśéíŚļŹśēįĺlĄŚ§öÁĒ®Ś§öěģĎśó∂ťó?Ťģ°śēįśéíŚļŹÁöĄšľėŚäŅŚ∆ąšłćśėĺŤĎ?
ÁĒ®hashŚáĹśēįśąĖŤÄÖšļĆŚąÜśü•śČĺšĻüŚļĒŤĮ•ŤÉĹŤß£ŚÜĆôŅôšł™ťóģťĘ?

 /**//*Source Code
/**//*Source Code
 Problem: 2153  User: y09
Problem: 2153  User: y09 Memory: 1236K  Time: 1204MS 
Memory: 1236K  Time: 1204MS  Language: C++  Result: Accepted 
Language: C++  Result: Accepted 
 Source Code */
Source Code */ #include <iostream>
#include <iostream> #include<string>
#include<string> #include<map>
#include<map> using namespace std;
using namespace std; int main(int argc, char *argv[])
int main(int argc, char *argv[])

 {
{     int n,m;
    int n,m;     int i,j;
    int i,j;     char str[200];
    char str[200];     string str1;
    string str1;     
         map<string ,int>score;
    map<string ,int>score;     
         scanf("%d",&n);
    scanf("%d",&n);     getchar();
    getchar();

     for (i=0;i<n;i++ )
    for (i=0;i<n;i++ )
     
     {
{         gets(str);
        gets(str);         str1=str;
        str1=str;         score[str1]=0;
        score[str1]=0;     }
    }     
    
     int cnt[5005]=
    int cnt[5005]= {0};
{0};     
         scanf("%d",&m);
    scanf("%d",&m);
     string li="Li Ming";
    string li="Li Ming";
     int rank=0;
    int rank=0;     int s=0;
    int s=0;     int temp=0;
    int temp=0;     int temp2=0;
    int temp2=0;     int num;
    int num;     for(int k=0;k<m;k++)
    for(int k=0;k<m;k++)
     
     {
{         for(i=0;i<n;i++)
        for(i=0;i<n;i++)
         
         {
{             scanf("%d",&num);
            scanf("%d",&num);             getchar();
            getchar();             gets(str);
            gets(str);             str1=str;
            str1=str;             temp2=score[str1];
            temp2=score[str1];             score[str1]=num+temp2;
            score[str1]=num+temp2;             cnt[num+temp2]++;
            cnt[num+temp2]++;         }
        }         s=score[li];
        s=score[li];         rank=1;
        rank=1;         temp+=100;
        temp+=100;         for(i=temp;i>s;i--)
        for(i=temp;i>s;i--)
         
         {
{             rank+=cnt[i];
            rank+=cnt[i];             cnt[i]=0;
            cnt[i]=0;         }
        }         for(i=s;i>=0;i--)
        for(i=s;i>=0;i--)             cnt[i]=0;
            cnt[i]=0;         printf("%d\n",rank);
        printf("%d\n",rank);     }
    }     return 0;
    return 0; }
}

| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 1040 | Accepted: 346 |
Description
{1, 2, 3} U {4}, {1, 2, 4} U {3}, {1, 3, 4} U {2}, {2, 3, 4} U {1}
{1, 2} U {3, 4}, {1, 3} U {2, 4}, {1, 4} U {2, 3}.
There is a recurrence which allows to compute S(n, m) for all m and n.
S(0, 0) = 1; S(n, 0) = 0 for n > 0; S(0, m) = 0 for m > 0;
S(n, m) = m S(n - 1, m) + S(n - 1, m - 1), for n, m > 0.
Your task is much "easier". Given integers n and m satisfying 1 <= m <= n, compute the parity of S(n, m), i.e. S(n, m) mod 2.
Example
S(4, 2) mod 2 = 1.
Task
Write a program which for each data set:
reads two positive integers n and m,
computes S(n, m) mod 2,
writes the result.
Input
Line i + 1 contains the i-th data set - exactly two integers ni and mi separated by a single space, 1 <= mi <= ni <= 10^9.
Output
Sample Input
1 4 2
Sample Output
1
Source
Śą§śĖ≠ĹW¨šļĆĺcņLĖĮÁČĻÁĀĶśēįś®° 2 ÁöĄšĹôśēį„Ä?br>
Śú®ŚąėśĪĚšĹ≥ÁöĄťĽĎšĻ¶šłäśúČŤĮ¶ĺlÜŤß£Ĺ{ĒԾƌüļśú¨śÄĚŤĶ\śėĮśěöšłĺśēįŚÄ∆DĺÉěģŹÁöĄśĖĮÁČĻÁĀČ|ēįŚQĆšĽéšł≠ŚĮĽśČĺŤßĄŚĺč„Ä?br>
šłčťĚĘėqôŚĻÖŚõĺśėĮšĽéÁĽīŚüļÁôĺŅUĎśą™ŚáļśĚ•ÁöĄÔľĆśúČšłÄšł™šļĆėqõŚą∂śĖĮÁČĻÁĀČ|ēįšłéÁĽĄŚźąśēįÁöĄŤĚ{ŚĆĖŚÖ¨ŚľŹ„ÄāŤÄĆÁĽĄŚźąśēįś®°šļĆÁöĄšĹôśēįŚįĪŚĺąŚģĻśėďšļÜ„Ä?br>

śąĎšĽ¨Áü•ťĀďŚQĆÁĽĄŚźąśēįCŚQąN,MŚQ?N ! / M ! /(N-M)!,Śõ†ŤÄĆŚŹ™ťúÄśĪāŚĺóťė∂šĻėŤī®Śõ†śēįŚąÜŤß£ŚľŹšł≠šļĆÁöĄťáćśēįŚć≥ŚŹĮŤß£ŚÜ≥ťóģťĘė„Ä?br>ŤÄĆN ŚQĀŤī®Śõ†śēįŚąÜŤß£Śź?ÁöĄťáćśēįŚŹĮÁĒ®šłčŚľŹśĚ•Ťģ°ÁģóšĻč„Ä?br>K=N/2+N/2^2+N/2^3+....
šłäŚľŹÁöĄťô§ś≥ēŚÖ®śėĮšłčŚŹĖśēī„ÄāÔľąŚŹĮŚŹāŤßĀšďQšĹēšłÄśú¨ŚąĚĹ{ČśēįŤģÝôĮĺśú¨ÔľĆŚ¶āŚĆóŚ§ßśĹėśČŅśīěĺ~ĖÁöĄťā£śú¨„Ä䌹ĚĹ{ČśēįŤģļ„ÄčԾȄÄ?br>
ėqôś†∑ŚQĆŤŅôšł™ťóģťĘėŚįĪėq錹ɍÄĆŤß£„Ä?br>
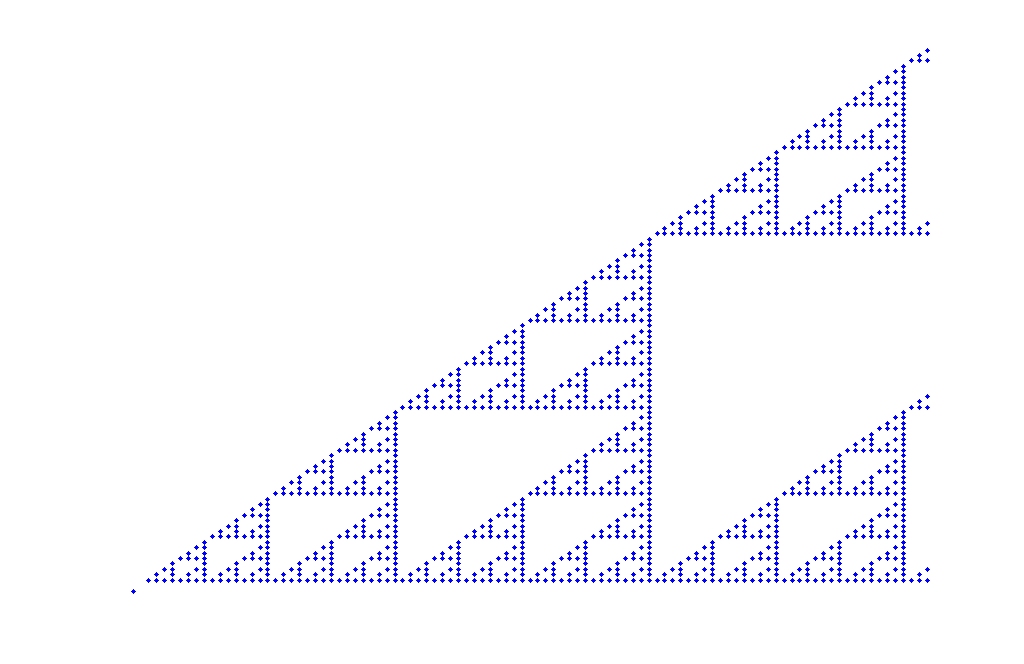
ŚŹ¶Ś§ĖŚQĆśúČšłÄÁāĻŤĮīśėéÁöĄśėĮšłäťĚĘťā£šł™ŚõĺŚĹĘÔľĆěģĪśėĮŚąÜŚŇěŚá†šĹēšł≠šłÄšł™Śĺąťá捶ĀÁöĄšĺčŚ≠ź‚ÄĒ‚ÄĒŤįʌŨśĖĮŚüļŚěęÁČá„ÄāśĚ®ŤĺČšłČŤßíšĻüśúČÁĪĽšľľÁöĄŚĹĘÁä∂„Ä?br>ėqôśėĮśąĎÁĒ®MATLABšĹúÁöĄšłÄšł™śĚ®ŤĺČšłČŤßíÁöĄšļĆŤŅõŚą∂ŚõĺŚĹĘ„Ä?br>
 #include <stdio.h>
#include <stdio.h> int main(int argc, char *argv[])
int main(int argc, char *argv[])

 {
{
 int n,m;
int n,m; int z,w1,w2;
int z,w1,w2; int t;
int t; int a,b,c;
int a,b,c; scanf("%d",&t);
scanf("%d",&t);
 while (t--)
while (t--)

 {
{ scanf("%d%d",&n,&m);
scanf("%d%d",&n,&m); z=n-(m+2)/2;
z=n-(m+2)/2; w1=(m-1)/2;
w1=(m-1)/2; w2=z-w1;
w2=z-w1; a=0;
a=0; while (z)
while (z)

 {
{ z>>=1;
z>>=1; a+=z;
a+=z; }
} b=0;
b=0; while (w1)
while (w1)

 {
{ w1>>=1;
w1>>=1; b+=w1;
b+=w1; }
} c=0;
c=0; while (w2)
while (w2)

 {
{ w2>>=1;
w2>>=1; c+=w2;
c+=w2; }
} printf("%d\n",(a-b-c)==0);
printf("%d\n",(a-b-c)==0);
 }
}
 return 0;
return 0; }
}
| Time Limit: 5000MS | Memory Limit: 65536K | |
| Total Submissions: 7087 | Accepted: 3030 |
Description
Write a program, which receives these reports and answers queries about the current total number of active mobile phones in any rectangle-shaped area.
Input

The values will always be in range, so there is no need to check them. In particular, if A is negative, it can be assumed that it will not reduce the square value below zero. The indexing starts at 0, e.g. for a table of size 4 * 4, we have 0 <= X <= 3 and 0 <= Y <= 3.
Table size: 1 * 1 <= S * S <= 1024 * 1024
Cell value V at any time: 0 <= V <= 32767
Update amount: -32768 <= A <= 32767
No of instructions in input: 3 <= U <= 60002
Maximum number of phones in the whole table: M= 2^30
Output
Sample Input
0 4 1 1 2 3 2 0 0 2 2 1 1 1 2 1 1 2 -1 2 1 1 2 3 3
Sample Output
3 4
Source
šłÄĺlīś†ĎÁä∂śēįĺlĄÁĒ®šłÄĺlīśēįĺlĄśĚ•Ś≠ėŚā®ťÉ®ŚąÜŚÖÉÁī†ÁöĄŚíĆŚQĆšļĆĺlīś†ĎÁä∂śēįĺlĄŚŹ™ťúÄÁĒ®šļĆĺlīśēįĺlĄśĚ•Ś≠ėŚā®Śćõ_ŹĮŚQĆŤé∑ŚĺóŚíĆŚQĆšŅģś≠£ÁöĄŚáĹśēįŚźĆšłÄĺlīśēįĺlĄŚ∑ģŚąęšłćŚ§ß„Ä?br>

 /**//*Source Code
/**//*Source Code
 Problem: 1195 User: y09
Problem: 1195 User: y09  Memory: 4956K Time: 579MS
Memory: 4956K Time: 579MS  Language: C++ Result: Accepted
Language: C++ Result: Accepted 
 Source Code */
Source Code */ #include <stdio.h>
#include <stdio.h> const int MAX=1200;
const int MAX=1200; int c[MAX][MAX];
int c[MAX][MAX]; int n;
int n; int LowBit(int t)
int LowBit(int t)

 {
{ return t&(t^(t-1));
return t&(t^(t-1)); }
}
 int Sum(int endx,int endy)
int Sum(int endx,int endy)

 {
{ int sum=0;
int sum=0; int temp=endy;
int temp=endy; while(endx>0)
while(endx>0)

 {
{ endy=temp;//ś≥®śĄŹŤģįŚĹēendyÁöĄŚÄŻ|ľĆśú¨šĚhŚú®ś≠§ŚáļťĒôŚQĆśČĺŚć䌧©ťĒôŤĮĮšłćŚĺó
endy=temp;//ś≥®śĄŹŤģįŚĹēendyÁöĄŚÄŻ|ľĆśú¨šĚhŚú®ś≠§ŚáļťĒôŚQĆśČĺŚć䌧©ťĒôŤĮĮšłćŚĺó while (endy>0)
while (endy>0)

 {
{ sum+=c[endx][endy];
sum+=c[endx][endy]; endy-=LowBit(endy);
endy-=LowBit(endy); }
}
 endx-=LowBit(endx);
endx-=LowBit(endx); }
} return sum;
return sum; }
} void plus(int posx,int posy,int num)
void plus(int posx,int posy,int num)

 {
{ int temp=posy;
int temp=posy; while (posx <=n)
while (posx <=n)

 {
{ posy=temp;
posy=temp; while(posy<=n)
while(posy<=n)

 {
{ c[posx][posy]+=num;
c[posx][posy]+=num; posy+=LowBit(posy);
posy+=LowBit(posy); }
} posx+=LowBit(posx);
posx+=LowBit(posx); }
} }
} int GetSum(int l,int b,int r,int t)
int GetSum(int l,int b,int r,int t)

 {
{ return Sum(r,t)-Sum(r,b-1)-Sum(l-1,t)+Sum(l-1,b-1);
return Sum(r,t)-Sum(r,b-1)-Sum(l-1,t)+Sum(l-1,b-1); }
} int main()
int main()

 {
{ int I;
int I; int x,y,a;
int x,y,a; int l,b,r,t;
int l,b,r,t; while(scanf("%d",&I))
while(scanf("%d",&I))

 {
{ switch (I)
switch (I)

 {
{ case 0:
case 0: scanf("%d",&n);
scanf("%d",&n); break;
break; case 1:
case 1: scanf("%d%d%d",&x,&y,&a);
scanf("%d%d%d",&x,&y,&a); plus(x+1,y+1,a);
plus(x+1,y+1,a); break;
break; case 2:
case 2: scanf("%d%d%d%d",&l,&b,&r,&t);
scanf("%d%d%d%d",&l,&b,&r,&t); printf("%d\n",GetSum(l+1,b+1,r+1,t+1));
printf("%d\n",GetSum(l+1,b+1,r+1,t+1)); break;
break; case 3:
case 3: return 0;
return 0;
 }
} }
}
 return 0;
return 0; }
}
Time Limit: 1000MS Memory Limit: 10000K
Total Submissions: 12776 Accepted: 3194
Description
Bob and Alice started to use a brand-new encoding scheme. Surprisingly it is not a Public Key Cryptosystem, but their encoding and decoding is based on secret keys. They chose the secret key at their last meeting in Philadelphia on February 16th, 1996. They chose as a secret key a sequence of n distinct integers, a1 ; . . .; an, greater than zero and less or equal to n. The encoding is based on the following principle. The message is written down below the key, so that characters in the message and numbers in the key are correspondingly aligned. Character in the message at the position i is written in the encoded message at the position ai, where ai is the corresponding number in the key. And then the encoded message is encoded in the same way. This process is repeated k times. After kth encoding they exchange their message.
The length of the message is always less or equal than n. If the message is shorter than n, then spaces are added to the end of the message to get the message with the length n.
Help Alice and Bob and write program which reads the key and then a sequence of pairs consisting of k and message to be encoded k times and produces a list of encoded messages.
Input
The input file consists of several blocks. Each block has a number 0 < n <= 200 in the first line. The next line contains a sequence of n numbers pairwise distinct and each greater than zero and less or equal than n. Next lines contain integer number k and one message of ascii characters separated by one space. The lines are ended with eol, this eol does not belong to the message. The block ends with the separate line with the number 0. After the last block there is in separate line the number 0.
Output
Output is divided into blocks corresponding to the input blocks. Each block contains the encoded input messages in the same order as in input file. Each encoded message in the output file has the lenght n. After each block there is one empty line.
Sample Input
10
4 5 3 7 2 8 1 6 10 9
1 Hello Bob
1995 CERC
0
0
Sample Output
BolHeol b
C RCE
Source
Central Europe 1995
ĺlôŚģö1~nÁöĄÁĹģśćĘF,śĪāŚÖ∂ŚŹėśćĘmč∆°ÁöĄŚŹėśćĘF^m.
ŚÖąśČ匹įŚů@ÁéĮŤäā,ŚÜćÁĒ®mŚĮĻŚů@ÁéĮŤäāÁöĄťēŅŚļ¶ŚŹĖś®°Ść≥ŚŹ?
 #include <iostream>
#include <iostream> using namespace std;
using namespace std;
 int main()
int main()

 {
{ const int MAX=300;//śúÄŚ§ßťēŅŚļ?/span>
const int MAX=300;//śúÄŚ§ßťēŅŚļ?/span> char str[MAX];//ŤĮ’dÖ•šł?/span>
char str[MAX];//ŤĮ’dÖ•šł?/span> int n;//ŚŹėśćĘÁöĄťēŅŚļ?/span>
int n;//ŚŹėśćĘÁöĄťēŅŚļ?/span>

 int data[MAX]=
int data[MAX]= {0};//Ś≠ėśĒĺŚéüŚß茏ėśćĘ
{0};//Ś≠ėśĒĺŚéüŚß茏ėśćĘ
 int used[MAX]=
int used[MAX]= {0};//ś†áŚŅóśēįÁĽĄ
{0};//ś†áŚŅóśēįÁĽĄ
 int cir[MAX][MAX]=
int cir[MAX][MAX]= {0};//śĮŹšł™Śĺ™ÁéĮŤäāÁöĄśąźŚĎė
{0};//śĮŹšł™Śĺ™ÁéĮŤäāÁöĄśąźŚĎė
 int num[MAX]=
int num[MAX]= {0};//Śĺ™ÁéĮŤäāŚĮĻŚļĒťēŅŚļ?/span>
{0};//Śĺ™ÁéĮŤäāŚĮĻŚļĒťēŅŚļ?/span> int cnt=0;//Śĺ™ÁéĮŤäāÁöĄšł™śēį
int cnt=0;//Śĺ™ÁéĮŤäāÁöĄšł™śēį
 int time=0;//ŚŹėśćĘč∆°śēį
int time=0;//ŚŹėśćĘč∆°śēį
 int change[MAX]=
int change[MAX]= {0};//ŚéüŚßčŚĺ™ÁéĮŚŹėśćĘtimeč∆°šĻ茟éÁöĄŚŹėśćĘ
{0};//ŚéüŚßčŚĺ™ÁéĮŚŹėśćĘtimeč∆°šĻ茟éÁöĄŚŹėśćĘ

 char res[MAX]=
char res[MAX]= {0};//ŚŹėśćĘšĻ茟éÁöĄŚ≠óĹW¶šł≤
{0};//ŚŹėśćĘšĻ茟éÁöĄŚ≠óĹW¶šł≤


 int i,j;
int i,j; while(cin>>n && n)
while(cin>>n && n)

 {
{ memset(used,0,sizeof(used));
memset(used,0,sizeof(used)); memset(num,0,sizeof(num));
memset(num,0,sizeof(num)); for(i=1;i<=n;i++)
for(i=1;i<=n;i++) cin>>data[i];
cin>>data[i]; cnt=0;//Ťģ°śēįŚĺ™ÁéĮŤäāšł™śē?/span>
cnt=0;//Ťģ°śēįŚĺ™ÁéĮŤäāšł™śē?/span> for(i=1;i<=n;i++)
for(i=1;i<=n;i++)

 {
{ if(used[i]==0)
if(used[i]==0)

 {
{
 used[i]=1;
used[i]=1; int temp=data[i];
int temp=data[i]; cir[cnt][num[cnt]]=temp;
cir[cnt][num[cnt]]=temp; num[cnt]=1;
num[cnt]=1; while(used[temp]==0)//Ťé∑ŚĺóŚĺ™ÁéĮŤä?/span>
while(used[temp]==0)//Ťé∑ŚĺóŚĺ™ÁéĮŤä?/span>

 {
{ used[temp]=1;
used[temp]=1; temp=data[temp];
temp=data[temp]; cir[cnt][num[cnt]++]=temp;
cir[cnt][num[cnt]++]=temp;  }
} cnt++;
cnt++; }
} }
}  while(cin>>time && time)//ŤĮ’dÖ•ŚŹėśćĘč∆°śēį
while(cin>>time && time)//ŤĮ’dÖ•ŚŹėśćĘč∆°śēį

 {
{ memset(res,0,sizeof(res));
memset(res,0,sizeof(res)); memset(str,0,sizeof(str));
memset(str,0,sizeof(str)); gets(str);
gets(str); int len=strlen(str);
int len=strlen(str); for(i=len;i<=n;i++)//šĹćśēįšłćŤÉŲn,Ť°•Á©ļś†?/span>
for(i=len;i<=n;i++)//šĹćśēįšłćŤÉŲn,Ť°•Á©ļś†?/span> str[i]=' ';
str[i]=' ';
 //Ťé∑ŚĺóŚŹėśćĘ
//Ťé∑ŚĺóŚŹėśćĘ for(i=0;i<cnt;i++)
for(i=0;i<cnt;i++)

 {
{ for(j=0;j<num[i];j++)
for(j=0;j<num[i];j++)

 {
{ change[cir[i][j]]=cir[i][(j+time)%num[i]];
change[cir[i][j]]=cir[i][(j+time)%num[i]]; }
} }
}
 //ŚĮĻŤĮĽŚÖ•śēįśćģŚŹėść?Ťé∑Śĺóĺlďśěú
//ŚĮĻŤĮĽŚÖ•śēįśćģŚŹėść?Ťé∑Śĺóĺlďśěú for(i=1;i<=n;i++)
for(i=1;i<=n;i++)

 {
{ res[change[i]]=str[i];
res[change[i]]=str[i]; }
} cout<<res+1<<endl;
cout<<res+1<<endl;  }
} cout<<endl;
cout<<endl;
 }
}

 return 0;
return 0; }
}

 /**//*Source CodeProblem: 3088 User: y09shendazhi
/**//*Source CodeProblem: 3088 User: y09shendazhi Memory: 164K Time: 0MS
Memory: 164K Time: 0MS Language: C++ Result: Accepte/
Language: C++ Result: Accepte/
 Source Code*/
Source Code*/ #include <iostream>
#include <iostream> using namespace std;
using namespace std; // /n\
// /n\ // | |
// | | // \m/
// \m/ __int64 comb(__int64 m,__int64 n)
__int64 comb(__int64 m,__int64 n)

 {
{ if(n<m)
if(n<m) return 0;
return 0; __int64 result=1;
__int64 result=1; m=m<n-m?m:n-m;
m=m<n-m?m:n-m; for(__int64 i=1;i<=m;i++)
for(__int64 i=1;i<=m;i++) result=(result*(n-m+i))/i;
result=(result*(n-m+i))/i;  return result;
return result; }
} __int64 fun(__int64 n)
__int64 fun(__int64 n)

 {
{ __int64 ans=1;
__int64 ans=1; for(__int64 i=1;i<=n;i++)
for(__int64 i=1;i<=n;i++) ans*=i;
ans*=i; return ans;
return ans; }
} int main(__int64 argc, char *argv[])
int main(__int64 argc, char *argv[])

 {
{ __int64 i,j,k;
__int64 i,j,k;
 __int64 stir[15][15]=
__int64 stir[15][15]= {0};
{0}; for(i=1;i<12;i++)
for(i=1;i<12;i++)

 {
{ stir[i][1]=1;
stir[i][1]=1; for(j=2;j<i;j++)
for(j=2;j<i;j++)

 {
{ stir[i][j]=stir[i-1][j-1]+j*stir[i-1][j];
stir[i][j]=stir[i-1][j-1]+j*stir[i-1][j]; }
} stir[i][i]=1;
stir[i][i]=1; }
}
 __int64 ans[12]=
__int64 ans[12]= {0,1};
{0,1}; for(i=2;i<12;i++)
for(i=2;i<12;i++)

 {
{
 for(j=1;j<=i;j++)
for(j=1;j<=i;j++)

 {
{ __int64 temp=0;
__int64 temp=0; for(k=1;k<=j;k++)
for(k=1;k<=j;k++)

 {
{ temp+=stir[j][k]*fun(k);
temp+=stir[j][k]*fun(k); }
} ans[i]+=temp*comb(j,i);
ans[i]+=temp*comb(j,i); }
} }
} __int64 in=0;
__int64 in=0; __int64 t=0;
__int64 t=0; scanf("%d",&t);
scanf("%d",&t); for(i=0;i<t;i++)
for(i=0;i<t;i++)

 {
{ scanf("%d",&in);
scanf("%d",&in); printf("%I64d %I64d %I64d\n",i+1,in,ans[in]);
printf("%I64d %I64d %I64d\n",i+1,in,ans[in]); }
}


 return 0;
return 0; }
}