|
|
思路：先求第一個的天數，然后用這個天數求第二個的表示方式，個人覺得不是水題
#include<stdio.h>
#include<string.h>
char hm[19][7]={"pop","no","zip","zotz","tzec","xul","yoxkin","mol","chen","yax",
"zac","ceh","mac","kankin","muan","pax","koyab","cumhu","uayet"};
char tm[20][9]={"imix","ik","akbal","kan","chicchan","cimi","manik","lamat","muluk","ok",
"chuen","eb","ben","ix","mem","cib","caban","eznab","canac","ahau"};
int main()
{
int i,m,n,day,year;
char month[9];
scanf("%d",&n);
printf("%d\n",n);
while (n--)
{
scanf("%d.%s%d",&day,month,&year);
for(i=0; i<19; i++)
if(strcmp(hm[i],month) == 0)
{
m=365*year+20*i+day;
break;
}
printf("%d %s %d\n",m%260%13+1,tm[m%20],m/260);
}
return 0;
}
此程序耗費我盡3個小時之久，原因是做題前的規劃沒做好，一直沒有想到整體排序的好辦法，最后還是用了注意匹配的方法才解決了問題，我不知道為什么用冒泡不行，第一個字符串總是亂碼。我覺得整體思路還是比較清晰的，只是方法可能有點傻，效率還行。 C 編譯器 : 172K 0MS
 #include <stdio.h>
#include <string.h>
typedef struct DNA
   {
 char str[50]; // 存儲字符串
int count[2]; // [0] [1]都存放串的逆序數
 }DNA; // [1]中作為參考,用來和排序后的[0]匹配
int main()
{
int i=0,j,k=0,n,m,temp;
DNA or[100];
scanf("%d%d",&n,&m);
while (k<m) //獲得數據并求各自逆序數
  {
scanf("%s",&or[k].str);
or[k].count[0]=0; // 此步不能忘
for (i=0; i<n; i++)
for (j=i+1; j<n; j++)
if (or[k].str[i] > or[k].str[j])
or[k].count[0]++;
k++;
 }
for (i=0; i<m; i++)
or[i].count[1]=or[i].count[0]; // 原逆序數存放順序
for (i=1; i<m; i++) // 對于各組串的逆序數進行排序,count[0]內容已打亂
{
k=i-1;
for (j=i; j<m; j++)
if (or[j].count[0] < or[k].count[0])
k=j;
temp=or[i-1].count[0];
or[i-1].count[0]=or[k].count[0];
or[k].count[0]=temp;
} // 這是典型的選擇排序,只是對[0]單元的處理,穩定與否沒關系
for (i=0; i<m; i++)
for (j=0; j<m; j++)
if (or[i].count[0] == or[j].count[1]) // [0] 和 [1] 中逐一相比較
{
or[j].count[1]=-1; // 此步是相等時順序不變的保證,相當于做了訪問標記!
printf("%s\n",or[j].str);
}
return 0;
}
典型的 閱讀理解題 , 讀懂意思基本上思路就出來了，恰巧又是一道中文題，這里用枚舉，其他不解釋。
#include <stdio.h>
int main()
{
int i,a,b,c,d,days=0;
while(1)
{
days++;
scanf("%d%d%d%d",&a,&b,&c,&d);
if (a+b+c+d == -4) break;
for (i=d+1; ; i++) // pay attention: from d+1
{
if ((i-a)%23==0)
if ((i-b)%28==0)
if ((i-c)%33==0)
{
printf("Case %d: the next triple peak occurs in %ld days.\n",days,i-d);
break;
}
}
}
return 0;
}
Description
Fred Mapper is considering purchasing some land in Louisiana to build his house on. In the process of investigating the land, he learned that the state of Louisiana is actually shrinking by 50 square miles each year, due to erosion caused by the Mississippi River. Since Fred is hoping to live in this house the rest of his life, he needs to know if his land is going to be lost to erosion. After doing more research, Fred has learned that the land that is being lost forms a semicircle. This semicircle is part of a circle centered at (0,0), with the line that bisects the circle being the X axis. Locations below the X axis are in the water. The semicircle has an area of 0 at the beginning of year 1. (Semicircle illustrated in the Figure.)
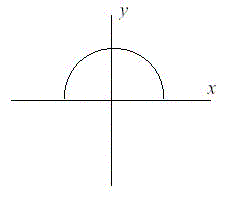
Input
The first line of input will be a positive integer indicating how many data sets will be included (N). Each of the next N lines will contain the X and Y Cartesian coordinates of the land Fred is considering. These will be floating point numbers measured in miles. The Y coordinate will be non-negative. (0,0) will not be given.
Output
For each data set, a single line of output should appear. This line should take the form of: “Property N: This property will begin eroding in year Z.” Where N is the data set (counting from 1), and Z is the first year (start from 1) this property will be within the semicircle AT THE END OF YEAR Z. Z must be an integer. After the last data set, this should print out “END OF OUTPUT.”
把題意弄明白，就知道這道題是水題了，由坐標 (0,0) 開始，以半圓為形狀每年侵蝕50 平方 miles ，問你從 (0,0) 開始到 (x,y) 結束需要多長時間，水題不需要太關注效率，所以變量定義上沒有深究，其他不解釋。
編譯器 C + + :
#include <iostream>
using namespace std;
#define PI 3.1415926
int main()
{
int n,i=0,year;
double x,y,area;
cin>>n;
while (i<n)
{
cin>>x>>y;
area = 0.5 * PI * (x*x+y*y); // semicircle area equation
year = area/50;
printf("Property %d: This property will begin eroding in year %d.\n",i+1,year+1);
i++;
}
printf("END OF OUTPUT.\n");
return 0;
}
正宗水題，就是輸入12個浮點數，讓你求平均值，不解釋。
#include<stdio.h>
int main()
{
float i=0,m,s=0;
for(;i<12;i++)
{
scanf("%f",&m);
s+=m;
}
printf("$%.2f\n",s/12);
return 0;
}
正宗水題，題目把最主要的公式都給你了，只要計算1/2+1/3+1/4+......+1/(n+1) >= x中最小的n值即可，我這里的cards用的是整形，注意底下一定要乘以1.0，否則會讓你調試的生不如死的，要不你就讓cards 是浮點型，其他的不解釋。
#include<stdio.h>
int main()
{
int cards;
float length,c;
for(scanf("%f",&c); c!=0.0; scanf("%f",&c))
{
for(cards=0,length=0; length<c; )
{
cards++;
length+=1/(cards*1.0+1);
}
printf("%d card(s)\n",cards);
}
return 0;
} //180K 0MS
事先申明，該程序雖然AC，但是效率極其低下，低下到讓人發指的程度，我也不知道為什么。估計是用了STL的原因，具體我也說不清楚。其實思路不難，就是將字符轉化成對應數字，然后將結果存放在一個整型向量中，接收字符串用的是字符串向量，處理的時候跟一般的字符串處理時一模一樣的。處理結束之后要進行字典排序，顯然要用排序函數，可以用冒泡，選擇，快排，甚至是Hash，但是據說STL的sort 效率比快排還要快。源程序后附加了MSDN上的一些簡單解釋。沒有翻譯！
Description
Businesses like to have memorable telephone numbers. One way to make a telephone number memorable is to have it spell a memorable word or phrase. For example, you can call the University of Waterloo by dialing the memorable TUT-GLOP. Sometimes only part of the number is used to spell a word. When you get back to your hotel tonight you can order a pizza from Gino's by dialing 310-GINO. Another way to make a telephone number memorable is to group the digits in a memorable way. You could order your pizza from Pizza Hut by calling their ``three tens'' number 3-10-10-10.
The standard form of a telephone number is seven decimal digits with a hyphen between the third and fourth digits (e.g. 888-1200). The keypad of a phone supplies the mapping of letters to numbers, as follows:
A, B, and C map to 2
D, E, and F map to 3
G, H, and I map to 4
J, K, and L map to 5
M, N, and O map to 6
P, R, and S map to 7
T, U, and V map to 8
W, X, and Y map to 9
There is no mapping for Q or Z. Hyphens are not dialed, and can be added and removed as necessary. The standard form of TUT-GLOP is 888-4567, the standard form of 310-GINO is 310-4466, and the standard form of 3-10-10-10 is 310-1010.
Two telephone numbers are equivalent if they have the same standard form. (They dial the same number.)
Your company is compiling a directory of telephone numbers from local businesses. As part of the quality control process you want to check that no two (or more) businesses in the directory have the same telephone number.
Input
The input will consist of one case. The first line of the input specifies the number of telephone numbers in the directory (up to 100,000) as a positive integer alone on the line. The remaining lines list the telephone numbers in the directory, with each number alone on a line. Each telephone number consists of a string composed of decimal digits, uppercase letters (excluding Q and Z) and hyphens. Exactly seven of the characters in the string will be digits or letters.
Output
Generate a line of output for each telephone number that appears more than once in any form. The line should give the telephone number in standard form, followed by a space, followed by the number of times the telephone number appears in the directory. Arrange the output lines by telephone number in ascending lexicographical order. If there are no duplicates in the input print the line:
No duplicates.
C++ 編譯器:
#include <iostream>
#include <string>
#include <vector>
#include <algorithm> // STL sort function
using namespace std;
char map[] = "2223334445556667#77888999#";
//ABCDEFGHIJKLMNOPQRSTUVWXYZ
void visited(char &ch) // visit and format strings
{
if (ch >= 'A' && ch <= 'Z')
ch=map[ch-'A']; // ch equals to its real number
}
int main()
{
int N,i=0,j,flag=0;
string s;
vector<string> stored(100000); // be visited & stored (up to 100,000)
cin>>N;
vector<int> counter(N,1); // stored times
for (; i<N; i++)
{
cin>>s;
for (j=0; j<s.length(); j++) // MSDN
{
visited(s[j]);
if (s[j]!='-')
{
stored[i] += s[j];
if (stored[i].length()==3)
stored[i] += '-'; // 487 -[3] 3279
}
}
}
sort(stored.begin(),stored.begin()+N); // Quicker than QuickSort!
// should not used stored.end() !
i=0; j=1;
while (i<N)
{
while(stored[i] == stored[j])
{
counter[i]++;
j++;
flag=1;
}
i=j;
j++;
}
if (flag)
for (i=0; i<N; i++)
{
if (counter[i]>1)
cout<<stored[i]<<" "<<counter[i]<<endl;
} // must have { }
else cout<<"No duplicates."<<endl;
return 0;
}
Sort ：
Arranges the elements in a specified range into a nondescending order or according to an ordering criterion specified by a binary predicate.
template<class RandomAccessIterator>
void sort(
RandomAccessIterator _First,
RandomAccessIterator _Last
);
分類開篇語: 第一個程序搞了好幾天，發現了很多問題。POJ不保證按順序做且更新速度肯定不會很快。有些題自己做不出來借鑒別人的會注明出處。很多算法都需要從網上找，第一題的大浮點數相乘的核心算法就是這樣找來的。我心里明白，雖然AC了，但是邊緣數據處理的很粗糙，我自己都發現幾個bug了，但是依然AC了。
本題主要注意將字符串轉化為實際的數字然后借鑒數制的思想來進行大數相乘。
Description
Problems involving the computation of exact values of very large magnitude and precision are common. For example, the computation of the national debt is a taxing experience for many computer systems.
This problem requires that you write a program to compute the exact value of Rn where R is a real number ( 0.0 < R < 99.999 ) and n is an integer such that 0 < n <= 25.
Input
The input will consist of a set of pairs of values for R and n. The R value will occupy columns 1 through 6, and the n value will be in columns 8 and 9.
Output
The output will consist of one line for each line of input giving the exact value of R^n. Leading zeros should be suppressed in the output. Insignificant trailing zeros must not be printed. Don't print the decimal point if the result is an integer.
Sample Input
95.123 12
0.4321 20
5.1234 15
6.7592 9
98.999 10
1.0100 12
Sample Output
548815620517731830194541.899025343415715973535967221869852721
.00000005148554641076956121994511276767154838481760200726351203835429763013462401
43992025569.928573701266488041146654993318703707511666295476720493953024
29448126.764121021618164430206909037173276672
90429072743629540498.107596019456651774561044010001
1.126825030131969720661201
編譯器C++ 源碼:
#include <iostream>
#include <string>
using namespace std;
#define MAX 255
int getnum(string s,int *c) // get real number of R
{
int i=0,j=0,t[MAX];
memset(t,0,sizeof(int)*MAX); // a stores 0
while (i < 6) // R value 1 through 6
{
if (s[i] != '.')
{
t[j]=s[i]-'0';
j++;
}
i++;
} // a`s length = 5
for (j=0; j<5; j++)
c[j]=t[4-j]; // c stores in order from a
for (i=0; s[i] != '.'; i++); // find decimal point
return (5-i); // the position of . point
}
void multi(int *a,int *b) // big-multiplication
{
int i=0,j,r=0,t[MAX];
memset(t,0,sizeof(int)*MAX); // t stores 0
for (; i<5; i++)
for (j=0; j<255; j++)
t[i+j] += a[i]*b[j]; // core algorithms!
for (i=0; i<255; i++)
{
b[i]=(r+t[i])%10; // r always stores remainder
r=(r+t[i])/10; // b stores the result
}
} // basic algorithms of b-m
int main()
{
int i,j,d_pos,n,a[MAX],b[MAX];
string s;
while (cin>>s>>n)
{
memset(b,0,sizeof(int)*MAX);
memset(a,0,sizeof(int)*MAX);
d_pos=getnum(s,a);
getnum(s,b);
for (i=0; i<n-1; i++)
multi(a,b); // a is a loop invariant
for (i=254; !b[i]; i--); //find last non-zero
for (j=0; !b[j]; j++); // find first non-zero
for (; i >= n*d_pos; i--) // loop n times
cout<<b[i];
if (n*d_pos >= j+1) cout<<"."; //pay attention
for (i=n*d_pos-1; i>=j; i--)
cout<<b[i]; //from back formating output
cout<<endl;
}
return 0;
}
1. 計算復雜性 O
這是描述一種算法需要多少 Running time 的度量。（也有空間復雜性，但因為它們能相互轉換，所以通常我們就說時間復雜性。對于大小為 n 的輸入，我們用含 n 的簡化式子來表達。（所謂簡化式子，就是忽略系數、常數，僅保留最“大”的那部分）。
比如找出 n 個數中最大的一個，很簡單，就是把第一個數和第二個比，其中大的那個再和第三個比，依次類推，總共要比 n-1 次，我們記作 O(n) (對于 n 可以是很大很大的情況下，-1可以忽略不計了）。
再比如從小到大排好的 n 個數，從中找出等于 x 的那個。一種方法是按著順序從頭到尾一個個找，最好情況是第一個就是 x，最壞情況是比較了 n 次直最后一個，因此最壞情況下的計算復雜度也是 O(n)。還有一種方法：先取中間那個數和 x 比較，如偏大則在前一半數中找，如偏小則在后一半數中找，每次都是取中間的那個數進行比較，則最壞情況是 lg(n)/lg2。忽略系數lg2，算法復雜度是O(lgn)。
2. 計算復雜性的排序
根據含 n 的表達式隨 n 增大的增長速度，可以將它們排序：1 < lg(n) < n < nlg(n) < n^2 < ... < n^k (k是常數）< ... < 2^n （不用死記，想象它們的函數曲線，一看便明）。最后這個 2 的n 次方就是級數增長了，讀過棋盤上放麥粒故事的人都知道這個增長速度有多快。而之前的那些都是 n 的多項式時間的復雜度。為什么我們在這里忽略所有的系數、常數，例如 2*n^3+9*n^2 可以被簡化為 n^3？老師上課也沒有說原因，所以我也不知道。但是如果對對 (2*n^3+9*n^2)/(n^3) 求導，結果是0，仔細想想，我也沒有想出所以然來。
3. P 問題
對一個問題，凡是能找到計算復雜度可以表示為多項式的確定算法，這個問題就屬于 P (polynomial) 問題。
4. NP 問題
NP 中的 N 是指非確定的(non-deterministic）算法，這是這樣一種算法：
（1）猜一個答案。（2）驗證這個答案是否正確。（3）只要存在某次驗證，答案是正確的，則該算法得解。
NP (non-deterministic polynomial)問題就是指，用這樣的非確定的算法，驗證步驟（2）有多項式時間的計算復雜度的算法。
5. 問題的歸約
想象一下函數的映射是怎么一回事吧。這個概念需要弄懂。
大致就是這樣：找從問題1的所有輸入到問題2的所有輸入的對應，如果相應的，也能有問題2的所有輸出到問題1的所有輸出的對應，則若我們找到了問題2的解法，就能通過輸入、輸出的對應關系，得到問題1的解法。由此我們說問題1可歸約到問題2。
再給一個我找到的高端解釋：
問題歸約是人求解問題常用的策略，其把復雜的問題變換為若干需要同時處理的較為簡單的子問題后再加以分別求解。只有當這些子問題全部解決時，問題才算解決，問題的解答就由子問題的解答聯合構成。問題歸約可以遞歸地進行，直到把問題變換為本原問題的集合。所謂本原問題就是不可或不需再通過變換化簡的"原子"問題，本原問題的解可以直接得到或通過一個"黑箱"操作得到。
6. NP-Hard
有這樣一種問題，所有 NP 問題都可以歸約到這種問題，我們稱之為 NP-hard 問題。
7. NP完全問題 (NP-Complete)
如果一個問題既是 NP 問題又是 NP-Hard 問題，則它是 NP-Complete 問題。可滿足性問題就是一個 NP 完全問題，此外著名的給圖染色、哈密爾頓環、背包、貨郎問題都是 NP 完全問題。
解壓縮版本的Eclipse打開時遇到此類問題：
解決方法：
打開安裝目錄下的eclipse.config（或eclipse.ini）配置文件，大致的內容如下，
-startup
plugins/org.eclipse.equinox.launcher_1.0.200.v20090520.jar
--launcher.library
plugins/org.eclipse.equinox.launcher.win32.win32.x86_1.0.200.v20090519
-product
org.eclipse.epp.package.jee.product
--launcher.XXMaxPermSize
256M
-showsplash
org.eclipse.platform
--launcher.XXMaxPermSize
256m
-vmargs
-Dosgi.requiredJavaVersion=1.5
-Xms40m
-Xmx512m
其中的“Xmx512m” 改成“Xmx256m”
|