|
|
2012年8月22日
Sierpinski三角形

楊輝三角,二項式系數(shù)奇偶性的判定 C(k,n)| k&n==k , 或者比較n!與{k!,(n-k)!}中2的個數(shù)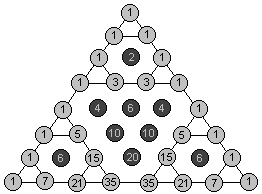
2012年4月13日
摘要: Code highlighting produced by Actipro CodeHighlighter (freeware)http://www.CodeHighlighter.com/-->#include <iostream>#include <math.h>using namespace std;const int... 閱讀全文
 #include <iostream> #include <iostream>
 using namespace std; using namespace std;

 const int MAXN=50*10005; const int MAXN=50*10005;
 const int MAXL=1005; const int MAXL=1005;
 const int K=26; const int K=26;

 struct Node struct Node
   { {
 Node *next[K], *fail; Node *next[K], *fail;
 int flag, id; int flag, id;
 void Init(int index) void Init(int index)
   { {
 id=index; id=index;
 flag=0; flag=0;
 fail=NULL; fail=NULL;
 for(int i=0; i<K; i++)next[i]=NULL; for(int i=0; i<K; i++)next[i]=NULL;
 } }
 }* Q[MAXN/2], *root, T[MAXN];// Q for queue, root&T for tree; }* Q[MAXN/2], *root, T[MAXN];// Q for queue, root&T for tree;

 int index=0; int index=0;
 Node * newNode() Node * newNode()
   { {
 T[index].Init(index); T[index].Init(index);
 return &T[index++]; return &T[index++];
 } }

  int tokind(char k) int tokind(char k) {return k-'a';} {return k-'a';}

 void insert(char *str) void insert(char *str)
   { {
 if(root==NULL) if(root==NULL)
 root=newNode(); root=newNode();

 Node *now=root; Node *now=root;
 for(int i=0; str[i]; i++) for(int i=0; str[i]; i++)
   { {
 int kind=tokind(str[i]); int kind=tokind(str[i]);
 if(now->next[kind]==NULL) if(now->next[kind]==NULL)
 now->next[kind]=newNode(); now->next[kind]=newNode();
 now=now->next[kind]; now=now->next[kind];
 } }
 now->flag++; now->flag++;
 } }

 void buildAC() void buildAC()
   { {
 int head=0, tail=0; int head=0, tail=0;
 root->fail=NULL; root->fail=NULL;

 Q[tail++]=root; Q[tail++]=root;
 while(head<tail) while(head<tail)
   { {
 Node *now=Q[head++]; Node *now=Q[head++];
 for(int i=0; i<K; i++) for(int i=0; i<K; i++)
   { {
 if(now->next[i]!=NULL) if(now->next[i]!=NULL)
   { {
 if(now==root)now->next[i]->fail=root; if(now==root)now->next[i]->fail=root;
 else else
   { {
 Node *p=now->fail; Node *p=now->fail;
 while(p->next[i]==NULL&&p!=root)p=p->fail; while(p->next[i]==NULL&&p!=root)p=p->fail;
 p=p->next[i]; p=p->next[i];
 now->next[i]->fail=(p==NULL)?root:p; now->next[i]->fail=(p==NULL)?root:p;
 } }
 Q[tail++]=now->next[i]; Q[tail++]=now->next[i];
 } }
 } }
 } }
 } }

 int query(char *str) int query(char *str)
   { {
 int res=0; int res=0;
 Node *p=root; Node *p=root;
 for(int i=0; str[i]; i++) for(int i=0; str[i]; i++)
   { {
 int kind=tokind(str[i]); int kind=tokind(str[i]);
 while(p->next[kind]==NULL&&p!=root)p=p->fail; while(p->next[kind]==NULL&&p!=root)p=p->fail;
 p=p->next[kind]; p=p->next[kind];
 p=(p==NULL)?root:p; p=(p==NULL)?root:p;
 Node *now=p; Node *now=p;
 while(now!=root&&now->flag!=-1) while(now!=root&&now->flag!=-1)
   { {
 res+=now->flag; res+=now->flag;
 now->flag=-1; now->flag=-1;
 now=now->fail; now=now->fail;
 } }
 } }
 return res; return res;
 } }

 int main() int main()
   { {
 //freopen ("in.txt", "r", stdin); //freopen ("in.txt", "r", stdin);
 int T; int T;
 scanf("%d", &T); scanf("%d", &T);
 while(T--) while(T--)
   { {
 int n; int n;
 root=NULL; root=NULL;
 scanf("%d",&n);getchar(); scanf("%d",&n);getchar();
 while(n--) while(n--)
   { {
 char str[55]; char str[55];
 scanf("%s",str); scanf("%s",str);
 insert(str); insert(str);
 } }
 buildAC(); buildAC();
 char ch[1000005]; char ch[1000005];
 scanf("%s",ch); scanf("%s",ch);
 printf("%d\n",query(ch)); printf("%d\n",query(ch));
 } }
 return 0; return 0;
 } }
2012年4月9日
1 #include <iostream> #include <iostream>
2 #include <vector> #include <vector>
3 #include <string> #include <string>
4 using namespace std; using namespace std;
5
6 #define madd(a,b) a=(a+b)%MOD #define madd(a,b) a=(a+b)%MOD
7
8 const int MOD=1000000007; const int MOD=1000000007;
9 const int MAXC=55, MAXH=75, MAXW=10, MAXB=15; const int MAXC=55, MAXH=75, MAXW=10, MAXB=15;
10 long g[MAXC], Comb[MAXC][MAXC]; long g[MAXC], Comb[MAXC][MAXC];
11 int dp[MAXW][MAXB][MAXC][MAXH][MAXW][2]; int dp[MAXW][MAXB][MAXC][MAXH][MAXW][2];
12
13 class SkewedPerspective class SkewedPerspective
14   { {
15
16 public: public:
17 int countThem(vector <int> cubes, int B, int w) int countThem(vector <int> cubes, int B, int w)
18   { {
19 int n=cubes.size(), total=0; int n=cubes.size(), total=0;
20 int i, j, k; int i, j, k;
21 for(i=0; i<n; i++) total+=cubes[i]; for(i=0; i<n; i++) total+=cubes[i];
22
23 for(i=0; i<=total; i++) for(i=0; i<=total; i++)
24 for(j=0; j<=i; j++) for(j=0; j<=i; j++)
25 Comb[i][j]=(j?(Comb[i-1][j]+Comb[i-1][j-1])%MOD:1); Comb[i][j]=(j?(Comb[i-1][j]+Comb[i-1][j-1])%MOD:1);
26 g[0]=1; g[0]=1;
27 for(i=0; i<n; i++) for(i=0; i<n; i++)
28 for(j=total; j; j--) for(j=total; j; j--)
29 for(k=1; k<=j && k<=cubes[i]; k++) for(k=1; k<=j && k<=cubes[i]; k++)
30 g[j]=(g[j]+g[j-k]*Comb[j][k])%MOD; g[j]=(g[j]+g[j-k]*Comb[j][k])%MOD;
31
32 long ans=0; long ans=0;
33 dp[1][0][0][0][0][0]=1; dp[1][0][0][0][0][0]=1;
34 for(int tower=1; tower<=w; tower++)for(int black=0; black<=B; black++) for(int tower=1; tower<=w; tower++)for(int black=0; black<=B; black++)
35 for(int color=0; color<=total; color++)for(int need=0; need<=total+black*2; need++) for(int color=0; color<=total; color++)for(int need=0; need<=total+black*2; need++)
36 for(int needOdd=0; needOdd<=tower; needOdd++)for(int lastBlack=0; lastBlack<2; lastBlack++) for(int needOdd=0; needOdd<=tower; needOdd++)for(int lastBlack=0; lastBlack<2; lastBlack++)
37   { {
38 int x=dp[tower][black][color][need][needOdd][lastBlack]; int x=dp[tower][black][color][need][needOdd][lastBlack];
39 if(!x)continue; if(!x)continue;
40 //get result //get result
41 if(black+color>0 && (B-black)*2+total-color>=need && total-color>=needOdd) if(black+color>0 && (B-black)*2+total-color>=need && total-color>=needOdd)
42 ans=(ans+g[color]*x)%MOD; ans=(ans+g[color]*x)%MOD;
43 //put colored //put colored
44 madd(dp[tower][black][color+1][need][needOdd][0], x); madd(dp[tower][black][color+1][need][needOdd][0], x);
45 if(lastBlack) continue; if(lastBlack) continue;
46 //put black //put black
47 int layer=black*2+color-(tower-1); int layer=black*2+color-(tower-1);
48 for(int blackSize=1; blackSize+black*2<=B*2; blackSize++) for(int blackSize=1; blackSize+black*2<=B*2; blackSize++)
49 if(blackSize%2==0) if(blackSize%2==0)
50 madd(dp[tower][black+blackSize/2][color][need][needOdd][1], x); madd(dp[tower][black+blackSize/2][color][need][needOdd][1], x);
51 else else
52   { {
53 if(!layer && blackSize==1) continue; //"b1bbbb" if(!layer && blackSize==1) continue; //"b1bbbb"
54 int needNow=(layer?layer-1:layer+1); int needNow=(layer?layer-1:layer+1);
55 if(need+needNow<=total+B*2) if(need+needNow<=total+B*2)
56 madd(dp[tower+1][black+(blackSize+1)/2][color][need+needNow][needOdd+needNow%2][1], x); madd(dp[tower+1][black+(blackSize+1)/2][color][need+needNow][needOdd+needNow%2][1], x);
57 } }
58
59 } }
60 return int(ans); return int(ans);
61 } }
62 }; };
63
64 int main() int main()
65   { {
66 SkewedPerspective a; SkewedPerspective a;
67  int cubes[]= int cubes[]= {1, 1, 0}; {1, 1, 0};
68 vector<int> t(cubes, cubes+3); vector<int> t(cubes, cubes+3);
69
70 cout<<a.countThem(t, 1, 2)<<endl; cout<<a.countThem(t, 1, 2)<<endl;
71 return 0; return 0;
72 } }
73
2011年5月21日
轉(zhuǎn)載自:http://www.iteye.com/topic/398782
很久很久以前,有一群人,他們決定用8個可以開合的晶體管來組合成不同的狀態(tài),以表示世界上的萬物。他們看到8個開關(guān)狀態(tài)是好的,于是他們把這稱為"字節(jié)"。
再后來,他們又做了一些可以處理這些字節(jié)的機(jī)器,機(jī)器開動了,可以用字節(jié)來組合出很多狀態(tài),狀態(tài)開始變來變?nèi)ァK麄兛吹竭@樣是好的,于是它們就這機(jī)器稱為"計算機(jī)"。
開始計算機(jī)只在美國用。八位的字節(jié)一共可以組合出256(2的8次方)種不同的狀態(tài)。
他們把其中的編號從0開始的32種狀態(tài)分別規(guī)定了特殊的用途,一但終端、打印機(jī)遇上約定好的這些字節(jié)被傳過來時,就要做一些約定的動作。遇上00x10, 終端就換行,遇上0x07, 終端就向人們嘟嘟叫,例好遇上0x1b, 打印機(jī)就打印反白的字,或者終端就用彩色顯示字母。他們看到這樣很好,于是就把這些0x20以下的字節(jié)狀態(tài)稱為"控制碼"。
他們又把所有的空格、標(biāo)點符號、數(shù)字、大小寫字母分別用連續(xù)的字節(jié)狀態(tài)表示,一直編到了第127號,這樣計算機(jī)就可以用不同字節(jié)來存儲英語的文字了。大家看到這樣,都感覺很好,于是大家都把這個方案叫做 ANSI 的"Ascii"編碼(American Standard Code for Information Interchange,美國信息互換標(biāo)準(zhǔn)代碼)。當(dāng)時世界上所有的計算機(jī)都用同樣的ASCII方案來保存英文文字。
后來,就像建造巴比倫塔一樣,世界各地的都開始使用計算機(jī),但是很多國家用的不是英文,他們的字母里有許多是ASCII里沒有的,為了可以在計算機(jī)保存他們的文字,他們決定采用127號之后的空位來表示這些新的字母、符號,還加入了很多畫表格時需要用下到的橫線、豎線、交叉等形狀,一直把序號編到了最后一個狀態(tài)255。從128到255這一頁的字符集被稱"擴(kuò)展字符集"。從此之后,貪婪的人類再沒有新的狀態(tài)可以用了,美帝國主義可能沒有想到還有第三世界國家的人們也希望可以用到計算機(jī)吧!
等中國人們得到計算機(jī)時,已經(jīng)沒有可以利用的字節(jié)狀態(tài)來表示漢字,況且有6000多個常用漢字需要保存呢。但是這難不倒智慧的中國人民,我們不客氣地把那些127號之后的奇異符號們直接取消掉, 規(guī)定:一個小于127的字符的意義與原來相同,但兩個大于127的字符連在一起時,就表示一個漢字,前面的一個字節(jié)(他稱之為高字節(jié))從0xA1用到0xF7,后面一個字節(jié)(低字節(jié))從0xA1到0xFE,這樣我們就可以組合出大約7000多個簡體漢字了。在這些編碼里,我們還把數(shù)學(xué)符號、羅馬希臘的字母、日文的假名們都編進(jìn)去了,連在 ASCII 里本來就有的數(shù)字、標(biāo)點、字母都統(tǒng)統(tǒng)重新編了兩個字節(jié)長的編碼,這就是常說的"全角"字符,而原來在127號以下的那些就叫"半角"字符了。
中國人民看到這樣很不錯,于是就把這種漢字方案叫做 "GB2312"。GB2312 是對 ASCII 的中文擴(kuò)展。
但是中國的漢字太多了,我們很快就就發(fā)現(xiàn)有許多人的人名沒有辦法在這里打出來,特別是某些很會麻煩別人的國家領(lǐng)導(dǎo)人。于是我們不得不繼續(xù)把 GB2312 沒有用到的碼位找出來老實不客氣地用上。
后來還是不夠用,于是干脆不再要求低字節(jié)一定是127號之后的內(nèi)碼,只要第一個字節(jié)是大于127就固定表示這是一個漢字的開始,不管后面跟的是不是擴(kuò)展字符集里的內(nèi)容。結(jié)果擴(kuò)展之后的編碼方案被稱為 GBK 標(biāo)準(zhǔn),GBK 包括了 GB2312 的所有內(nèi)容,同時又增加了近20000個新的漢字(包括繁體字)和符號。
后來少數(shù)民族也要用電腦了,于是我們再擴(kuò)展,又加了幾千個新的少數(shù)民族的字,GBK 擴(kuò)成了 GB18030。從此之后,中華民族的文化就可以在計算機(jī)時代中傳承了。
中國的程序員們看到這一系列漢字編碼的標(biāo)準(zhǔn)是好的,于是通稱他們叫做 "DBCS"(Double Byte Charecter Set 雙字節(jié)字符集)。在DBCS系列標(biāo)準(zhǔn)里,最大的特點是兩字節(jié)長的漢字字符和一字節(jié)長的英文字符并存于同一套編碼方案里,因此他們寫的程序為了支持中文處理,必須要注意字串里的每一個字節(jié)的值,如果這個值是大于127的,那么就認(rèn)為一個雙字節(jié)字符集里的字符出現(xiàn)了。那時候凡是受過加持,會編程的計算機(jī)僧侶們都要每天念下面這個咒語數(shù)百遍:
"一個漢字算兩個英文字符!一個漢字算兩個英文字符......"
因為當(dāng)時各個國家都像中國這樣搞出一套自己的編碼標(biāo)準(zhǔn),結(jié)果互相之間誰也不懂誰的編碼,誰也不支持別人的編碼,連大陸和臺灣這樣只相隔了150海里,使用著同一種語言的兄弟地區(qū),也分別采用了不同的 DBCS 編碼方案。當(dāng)時的中國人想讓電腦顯示漢字,就必須裝上一個"漢字系統(tǒng)",專門用來處理漢字的顯示、輸入的問題,但是那個臺灣的愚昧封建人士寫的算命程序就必須加裝另一套支持 BIG5 編碼的什么"倚天漢字系統(tǒng)"才可以用,裝錯了字符系統(tǒng),顯示就會亂了套!這怎么辦?而且世界民族之林中還有那些一時用不上電腦的窮苦人民,他們的文字又怎么辦?
真是計算機(jī)的巴比倫塔命題啊!
正在這時,大天使加百列及時出現(xiàn)了:一個叫 ISO (國際標(biāo)誰化組織)的國際組織決定著手解決這個問題。他們采用的方法很簡單:廢了所有的地區(qū)性編碼方案,重新搞一個包括了地球上所有文化、所有字母和符號的編碼!他們打算叫它"Universal Multiple-Octet Coded Character Set",簡稱 UCS, 俗稱 "UNICODE"。
UNICODE 開始制訂時,計算機(jī)的存儲器容量極大地發(fā)展了,空間再也不成為問題了。于是 ISO 就直接規(guī)定必須用兩個字節(jié),也就是16位來統(tǒng)一表示所有的字符,對于ascii里的那些"半角"字符,UNICODE 包持其原編碼不變,只是將其長度由原來的8位擴(kuò)展為16位,而其他文化和語言的字符則全部重新統(tǒng)一編碼。由于"半角"英文符號只需要用到低8位,所以其高8位永遠(yuǎn)是0,因此這種大氣的方案在保存英文文本時會多浪費一倍的空間。
這時候,從舊社會里走過來的程序員開始發(fā)現(xiàn)一個奇怪的現(xiàn)象:他們的strlen函數(shù)靠不住了,一個漢字不再是相當(dāng)于兩個字符了,而是一個!是的,從 UNICODE 開始,無論是半角的英文字母,還是全角的漢字,它們都是統(tǒng)一的"一個字符"!同時,也都是統(tǒng)一的"兩個字節(jié)",請注意"字符"和"字節(jié)"兩個術(shù)語的不同,"字節(jié)"是一個8位的物理存貯單元,而"字符"則是一個文化相關(guān)的符號。在UNICODE 中,一個字符就是兩個字節(jié)。一個漢字算兩個英文字符的時代已經(jīng)快過去了。
從前多種字符集存在時,那些做多語言軟件的公司遇上過很大麻煩,他們?yōu)榱嗽诓煌膰忆N售同一套軟件,就不得不在區(qū)域化軟件時也加持那個雙字節(jié)字符集咒語,不僅要處處小心不要搞錯,還要把軟件中的文字在不同的字符集中轉(zhuǎn)來轉(zhuǎn)去。UNICODE 對于他們來說是一個很好的一攬子解決方案,于是從 Windows NT 開始,MS 趁機(jī)把它們的操作系統(tǒng)改了一遍,把所有的核心代碼都改成了用 UNICODE 方式工作的版本,從這時開始,WINDOWS 系統(tǒng)終于無需要加裝各種本土語言系統(tǒng),就可以顯示全世界上所有文化的字符了。
但是,UNICODE 在制訂時沒有考慮與任何一種現(xiàn)有的編碼方案保持兼容,這使得 GBK 與UNICODE 在漢字的內(nèi)碼編排上完全是不一樣的,沒有一種簡單的算術(shù)方法可以把文本內(nèi)容從UNICODE編碼和另一種編碼進(jìn)行轉(zhuǎn)換,這種轉(zhuǎn)換必須通過查表來進(jìn)行。
如前所述,UNICODE 是用兩個字節(jié)來表示為一個字符,他總共可以組合出65535不同的字符,這大概已經(jīng)可以覆蓋世界上所有文化的符號。如果還不夠也沒有關(guān)系,ISO已經(jīng)準(zhǔn)備了UCS-4方案,說簡單了就是四個字節(jié)來表示一個字符,這樣我們就可以組合出21億個不同的字符出來(最高位有其他用途),這大概可以用到銀河聯(lián)邦成立那一天吧!
UNICODE 來到時,一起到來的還有計算機(jī)網(wǎng)絡(luò)的興起,UNICODE 如何在網(wǎng)絡(luò)上傳輸也是一個必須考慮的問題,于是面向傳輸?shù)谋姸?UTF(UCS Transfer Format)標(biāo)準(zhǔn)出現(xiàn)了,顧名思義,UTF8就是每次8個位傳輸數(shù)據(jù),而UTF16就是每次16個位,只不過為了傳輸時的可靠性,從UNICODE到UTF時并不是直接的對應(yīng),而是要過一些算法和規(guī)則來轉(zhuǎn)換。
受到過網(wǎng)絡(luò)編程加持的計算機(jī)僧侶們都知道,在網(wǎng)絡(luò)里傳遞信息時有一個很重要的問題,就是對于數(shù)據(jù)高低位的解讀方式,一些計算機(jī)是采用低位先發(fā)送的方法,例如我們PC機(jī)采用的 INTEL 架構(gòu),而另一些是采用高位先發(fā)送的方式,在網(wǎng)絡(luò)中交換數(shù)據(jù)時,為了核對雙方對于高低位的認(rèn)識是否是一致的,采用了一種很簡便的方法,就是在文本流的開始時向?qū)Ψ桨l(fā)送一個標(biāo)志符。如果之后的文本是高位在位,那就發(fā)送"FEFF",反之,則發(fā)送"FFFE"。不信你可以用二進(jìn)制方式打開一個UTF-X格式的文件,看看開頭兩個字節(jié)是不是這兩個字節(jié)?
講到這里,我們再順便說說一個很著名的奇怪現(xiàn)象:當(dāng)你在 windows 的記事本里新建一個文件,輸入"聯(lián)通"兩個字之后,保存,關(guān)閉,然后再次打開,你會發(fā)現(xiàn)這兩個字已經(jīng)消失了,代之的是幾個亂碼!呵呵,有人說這就是聯(lián)通之所以拼不過移動的原因。
其實這是因為GB2312編碼與UTF8編碼產(chǎn)生了編碼沖撞的原因。
從網(wǎng)上引來一段從UNICODE到UTF8的轉(zhuǎn)換規(guī)則:
Unicode
UTF-8
0000 - 007F
0xxxxxxx
0080 - 07FF
110xxxxx 10xxxxxx
0800 - FFFF
1110xxxx 10xxxxxx 10xxxxxx
例如"漢"字的Unicode編碼是6C49。6C49在0800-FFFF之間,所以要用3字節(jié)模板:1110xxxx 10xxxxxx 10xxxxxx。將6C49寫成二進(jìn)制是:0110 1100 0100 1001,將這個比特流按三字節(jié)模板的分段方法分為0110 110001 001001,依次代替模板中的x,得到:1110-0110 10-110001 10-001001,即E6 B1 89,這就是其UTF8的編碼。
而當(dāng)你新建一個文本文件時,記事本的編碼默認(rèn)是ANSI, 如果你在ANSI的編碼輸入漢字,那么他實際就是GB系列的編碼方式,在這種編碼下,"聯(lián)通"的內(nèi)碼是:
c1 1100 0001
aa 1010 1010
cd 1100 1101
a8 1010 1000
注意到了嗎?第一二個字節(jié)、第三四個字節(jié)的起始部分的都是"110"和"10",正好與UTF8規(guī)則里的兩字節(jié)模板是一致的,于是再次打開記事本時,記事本就誤認(rèn)為這是一個UTF8編碼的文件,讓我們把第一個字節(jié)的110和第二個字節(jié)的10去掉,我們就得到了"00001 101010",再把各位對齊,補(bǔ)上前導(dǎo)的0,就得到了"0000 0000 0110 1010",不好意思,這是UNICODE的006A,也就是小寫的字母"j",而之后的兩字節(jié)用UTF8解碼之后是0368,這個字符什么也不是。這就是只有"聯(lián)通"兩個字的文件沒有辦法在記事本里正常顯示的原因。
而如果你在"聯(lián)通"之后多輸入幾個字,其他的字的編碼不見得又恰好是110和10開始的字節(jié),這樣再次打開時,記事本就不會堅持這是一個utf8編碼的文件,而會用ANSI的方式解讀之,這時亂碼又不出現(xiàn)了。
2010年1月1日
 #include <iostream> #include <iostream>
 using namespace std; using namespace std;
 const int M=10; const int M=10;
 char map[2][M][M]; char map[2][M][M];
 bool vis[2][M][M]; bool vis[2][M][M];
  int dx[]= int dx[]= {1,0,-1,0}; {1,0,-1,0};
  int dy[]= int dy[]= {0,1,0,-1}; {0,1,0,-1};

 struct point struct point
   { {
 int layer; int layer;
 int x,y; int x,y;
 int time; int time;
 }Q[200]; }Q[200];

 bool BFS(int m,int n,int t) bool BFS(int m,int n,int t)
   { {
 point now,next; point now,next;
 now.layer=now.x=now.y=now.time=0; now.layer=now.x=now.y=now.time=0;
 int Front=0; int Front=0;
 int Near=1; int Near=1;
 Q[Front]=now; Q[Front]=now;
 vis[now.layer][now.x][now.y]=true; vis[now.layer][now.x][now.y]=true;
 while(Front<Near) while(Front<Near)
   { {
 now=Q[Front++]; now=Q[Front++];
 if(map[now.layer][now.x][now.y]=='P') if(map[now.layer][now.x][now.y]=='P')
   { {
 if(now.time<=t) if(now.time<=t)
 return true; return true;
 return false; return false;
 } }
 if(map[now.layer][now.x][now.y]=='#') if(map[now.layer][now.x][now.y]=='#')
 now.layer=!now.layer; now.layer=!now.layer;

 if(map[now.layer][now.x][now.y]=='P') if(map[now.layer][now.x][now.y]=='P')
   { {
 if(now.time<=t) if(now.time<=t)
 return true; return true;
 return false; return false;
 } }
 if(map[now.layer][now.x][now.y]=='*'||map[now.layer][now.x][now.y]=='#') if(map[now.layer][now.x][now.y]=='*'||map[now.layer][now.x][now.y]=='#')
 continue; continue;
 int k; int k;
 for(k=0;k<4;k++) for(k=0;k<4;k++)
   { {
 next.layer=now.layer; next.layer=now.layer;
 next.time=now.time+1; next.time=now.time+1;
 next.x=now.x+dx[k]; next.x=now.x+dx[k];
 next.y=now.y+dy[k]; next.y=now.y+dy[k];
 if(!vis[next.layer][next.x][next.y]&&next.x>=0&&next.x<m&&next.y>=0&&next.y<n) if(!vis[next.layer][next.x][next.y]&&next.x>=0&&next.x<m&&next.y>=0&&next.y<n)
   { {
 Q[Near++]=next; Q[Near++]=next;
 vis[next.layer][next.x][next.y]=true; vis[next.layer][next.x][next.y]=true;
 } }
 } }

 } }
 return false; return false;
 } }
 int main() int main()
   { {
 int T; int T;
 scanf("%d",&T); scanf("%d",&T);
 while(T--) while(T--)
   { {
 int m,n,t; int m,n,t;
 scanf("%d%d%d",&m,&n,&t); scanf("%d%d%d",&m,&n,&t);
 int i,j,k; int i,j,k;
 for(k=0;k<2;k++) for(k=0;k<2;k++)
   { {
 for(i=0;i<m;i++) for(i=0;i<m;i++)
   { {
 char s[M]; char s[M];
 scanf("%s",&s); scanf("%s",&s);
 for(j=0;j<n;j++) for(j=0;j<n;j++)
   { {
 map[k][i][j]=s[j]; map[k][i][j]=s[j];
 vis[k][i][j]=false; vis[k][i][j]=false;
 } }
 } }
 } }
 if(BFS(m,n,t)) if(BFS(m,n,t))
 printf("YES\n"); printf("YES\n");
 else else
 printf("NO\n"); printf("NO\n");
 } }
 system("pause"); system("pause");
 return 0; return 0;
 } }
 #include <iostream> #include <iostream>
 using namespace std; using namespace std;
 const int M=10; const int M=10;
 bool userow[M][M],usecol[M][M],useblock[M][M]; bool userow[M][M],usecol[M][M],useblock[M][M];
 int map[M][M]; int map[M][M];

  struct node struct node { {
 int x,y; int x,y;
 int num; int num;
 }sudu[M*M]; }sudu[M*M];

 int find(int x,int y) int find(int x,int y)
   { {
 int row=x/3; int row=x/3;
 int col=y/3; int col=y/3;
 return 3*row+col; return 3*row+col;
 } }

 bool dfs(int n,int cnt) bool dfs(int n,int cnt)
   { {
 if(n==cnt)return 1; if(n==cnt)return 1;
 int i; int i;
 for(i=1;i<M;i++) for(i=1;i<M;i++)
   { {
 if(!userow[sudu[n].x][i]&&!usecol[sudu[n].y][i]&&!useblock[find(sudu[n].x,sudu[n].y)][i]) if(!userow[sudu[n].x][i]&&!usecol[sudu[n].y][i]&&!useblock[find(sudu[n].x,sudu[n].y)][i])
   { {
 userow[sudu[n].x][i]=true; userow[sudu[n].x][i]=true;
 usecol[sudu[n].y][i]=true; usecol[sudu[n].y][i]=true;
 useblock[find(sudu[n].x,sudu[n].y)][i]=true; useblock[find(sudu[n].x,sudu[n].y)][i]=true;
 sudu[n].num=i; sudu[n].num=i;
 if(dfs(n+1,cnt)) if(dfs(n+1,cnt))
 return 1; return 1;
 userow[sudu[n].x][i]=false; userow[sudu[n].x][i]=false;
 usecol[sudu[n].y][i]=false; usecol[sudu[n].y][i]=false;
 useblock[find(sudu[n].x,sudu[n].y)][i]=false; useblock[find(sudu[n].x,sudu[n].y)][i]=false;
 sudu[n].num=0; sudu[n].num=0;

 } }
 } }
 return 0; return 0;

 } }

 int main() int main()
   { {
 int T; int T;
 scanf("%d",&T); scanf("%d",&T);
 while(T--) while(T--)
   { {
 memset(userow,false,sizeof(userow)); memset(userow,false,sizeof(userow));
 memset(usecol,false,sizeof(usecol)); memset(usecol,false,sizeof(usecol));
 memset(useblock,false,sizeof(useblock)); memset(useblock,false,sizeof(useblock));

 int i,j; int i,j;
 int cnt=0; int cnt=0;
 for(i=0;i<M-1;i++) for(i=0;i<M-1;i++)
   { {
 char mess[M]; char mess[M];
 scanf("%s",&mess); scanf("%s",&mess);
 for(j=0;j<M-1;j++) for(j=0;j<M-1;j++)
   { {
 map[i][j]=mess[j]-'0'; map[i][j]=mess[j]-'0';
 if(map[i][j]) if(map[i][j])
   { {
 userow[i][map[i][j]]=true; userow[i][map[i][j]]=true;
 usecol[j][map[i][j]]=true; usecol[j][map[i][j]]=true;
 useblock[find(i,j)][map[i][j]]=true; useblock[find(i,j)][map[i][j]]=true;
 } }
 else else
   { {
 sudu[cnt].x=i; sudu[cnt].x=i;
 sudu[cnt].y=j; sudu[cnt].y=j;
 sudu[cnt].num=0; sudu[cnt].num=0;
 cnt++; cnt++;
 } }

 } }

 } }

 dfs(0,cnt); dfs(0,cnt);

 for(i=0;i<cnt;i++) for(i=0;i<cnt;i++)
 map[sudu[i].x][sudu[i].y]=sudu[i].num; map[sudu[i].x][sudu[i].y]=sudu[i].num;

  for(i=0;i<M-1;i++) for(i=0;i<M-1;i++) { {
 for(j=0;j<M-1;j++) for(j=0;j<M-1;j++)
 printf("%d",map[i][j]); printf("%d",map[i][j]);
 printf("\n"); printf("\n");
 } }
 } }

 return 0; return 0;
 } }
2009年11月21日
摘要:
#include <iostream>using namespace std;const int maxn=200;const int INF=1000000;int g[maxn][maxn];int f[maxn][maxn];int r[maxn][maxn];in... 閱讀全文
2009年10月5日
 #include <iostream> #include <iostream>
 #include <algorithm> #include <algorithm>
 using namespace std; using namespace std;

 const int maxn=12; const int maxn=12;
 int n; int n;
 double p; double p;
 struct matrix struct matrix
   { {
 double m[2][2]; double m[2][2];
 }; };
 int mine[maxn]; int mine[maxn];
 matrix operator*(const matrix&a,const matrix&b) matrix operator*(const matrix&a,const matrix&b)
   { {
 matrix tmp; matrix tmp;
 int i,j,k; int i,j,k;
 for(i=0;i<2;i++) for(i=0;i<2;i++)
 for(j=0;j<2;j++) for(j=0;j<2;j++)
   { {
 tmp.m[i][j]=0; tmp.m[i][j]=0;
 for(k=0;k<2;k++) for(k=0;k<2;k++)
 tmp.m[i][j]+=a.m[i][k]*b.m[k][j]; tmp.m[i][j]+=a.m[i][k]*b.m[k][j];
 } }
 return tmp; return tmp;
 } }

 matrix power(int k) matrix power(int k)
   { {
 matrix tmp,res; matrix tmp,res;
 matrix A; matrix A;
 A.m[0][0]=p,A.m[0][1]=1-p,A.m[1][0]=1,A.m[1][1]=0; A.m[0][0]=p,A.m[0][1]=1-p,A.m[1][0]=1,A.m[1][1]=0;
 matrix B; matrix B;
 B.m[0][0]=1,B.m[0][1]=0,B.m[1][0]=0,B.m[1][1]=1; B.m[0][0]=1,B.m[0][1]=0,B.m[1][0]=0,B.m[1][1]=1;
 if(k==0) if(k==0)
 return B; return B;
 if(k==1) if(k==1)
 return A; return A;
 else else
   { {
 tmp=power(k/2); tmp=power(k/2);
 res=tmp*tmp; res=tmp*tmp;
 if(k%2==1) if(k%2==1)
 res=res*A; res=res*A;
 return res; return res;
 } }
 } }

 void slove(int n,double p) void slove(int n,double p)
   { {
 double a=1,b=0; double a=1,b=0;
 int i; int i;
 for(i=0;i<n;i++) for(i=0;i<n;i++)
 scanf("%d",&mine[i]); scanf("%d",&mine[i]);
 sort(mine,mine+n); sort(mine,mine+n);

 double f2=1.0,f1=0.0; double f2=1.0,f1=0.0;
 int now=1; int now=1;
 for(i=0;i<n;i++) for(i=0;i<n;i++)
   { {
 if((mine[i]-1)-now>=0) if((mine[i]-1)-now>=0)
   { {
 matrix tmp=power(mine[i]-1-now); matrix tmp=power(mine[i]-1-now);
 f2=(tmp.m[0][0]*f2+tmp.m[0][1]*f1)*(1-p); f2=(tmp.m[0][0]*f2+tmp.m[0][1]*f1)*(1-p);
 f1=0; f1=0;
 now=mine[i]+1; now=mine[i]+1;
 } }
 else else
   { {
 printf("%.7lf\n",0.0); printf("%.7lf\n",0.0);
 return; return;
 } }
 } }
 printf("%.7lf\n",f2); printf("%.7lf\n",f2);
 } }

 int main() int main()
   { {
 while(scanf("%d %lf",&n,&p)!=EOF) while(scanf("%d %lf",&n,&p)!=EOF)
 slove(n,p); slove(n,p);
 return 0; return 0;
 } }


 #include <iostream> #include <iostream>
 using namespace std; using namespace std;

 const int maxn=1005; const int maxn=1005;
 __int64 n,m; __int64 n,m;
 __int64 F[maxn]; __int64 F[maxn];
 int c[maxn][maxn]; int c[maxn][maxn];

 int cal(int n) int cal(int n)
   { {
 int t = 1; int t = 1;
 while (t <= n) t = t * 2 + 1; while (t <= n) t = t * 2 + 1;
 t = (t - 1) / 2; t = (t - 1) / 2;
 t = (t - 1) / 2; t = (t - 1) / 2;
 int sum = n - 1 - t; int sum = n - 1 - t;
  if (sum > 2 * t + 1) if (sum > 2 * t + 1)  { {
 sum = 2 * t + 1; sum = 2 * t + 1;
 } }
 return sum; return sum;
 } }

  void calc_c() void calc_c()  { {
 for (int i = 0; i < maxn; i++) for (int i = 0; i < maxn; i++)
   { {
 c[i][0] = c[i][i] = 1; c[i][0] = c[i][i] = 1;
 for (int j = 1; j < i; j++) for (int j = 1; j < i; j++)
   { {
 c[i][j] = (c[i - 1][j - 1] + c[i - 1][j]) % m; c[i][j] = (c[i - 1][j - 1] + c[i - 1][j]) % m;
 } }
 } }
 } }

 __int64 slove(int n) __int64 slove(int n)
   { {
 if(F[n]) if(F[n])
 return F[n]; return F[n];
 if(n==0||n==1) if(n==0||n==1)
 return 1; return 1;
 int left=cal(n); int left=cal(n);
 int right=(n-1)-left; int right=(n-1)-left;
 return F[n]=( (slove(left)*slove(right) )%m )*(__int64)c[n-1][left]%m; return F[n]=( (slove(left)*slove(right) )%m )*(__int64)c[n-1][left]%m;
 } }
 int main() int main()
   { {
 int T; int T;
 scanf("%d",&T); scanf("%d",&T);
 while(T--) while(T--)
   { {
 memset(F,0,sizeof(F)); memset(F,0,sizeof(F));
 scanf("%I64d%I64d",&n,&m); scanf("%I64d%I64d",&n,&m);
 calc_c(); calc_c();
 __int64 ans=slove(n); __int64 ans=slove(n);
 printf("%I64d\n",ans); printf("%I64d\n",ans);
 } }
 return 0; return 0;
 } }
|